2022年秋季北师版数学九年级上册期末复习检测B
试卷更新日期:2022-11-08 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )A、 B、 C、 D、2. 用配方法解方程x2-2x=2时,配方后正确的是( )A、 B、 C、 D、3. 如图,▱ABCD的对角线AC和BD相交于点O,下列说法正确的是( )
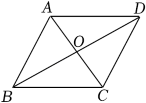 A、若OB=OD,则▱ABCD是菱形 B、若AC=BD,则▱ABCD是菱形 C、若OA=OD,则▱ABCD是菱形 D、若AC⊥BD,则▱ABCD是菱形4. 几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
A、若OB=OD,则▱ABCD是菱形 B、若AC=BD,则▱ABCD是菱形 C、若OA=OD,则▱ABCD是菱形 D、若AC⊥BD,则▱ABCD是菱形4. 几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )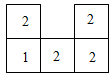 A、3 B、4 C、6 D、95. 如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )
A、3 B、4 C、6 D、95. 如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )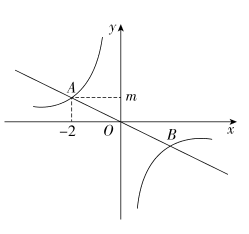 A、x<﹣2或x>2 B、﹣2<x<2 C、﹣2<x<0或x>2 D、x<﹣2或0<x<26. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( )
A、x<﹣2或x>2 B、﹣2<x<2 C、﹣2<x<0或x>2 D、x<﹣2或0<x<26. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( ) A、 B、 C、 D、7. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )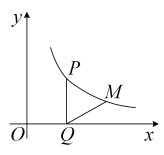 A、 B、 C、 D、48. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A、 B、 C、 D、48. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、9. 已知关于的一元二次方程的两根分别记为 , , 若 , 则的值为( )A、7 B、-7 C、6 D、-610. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )
A、 B、 C、 D、9. 已知关于的一元二次方程的两根分别记为 , , 若 , 则的值为( )A、7 B、-7 C、6 D、-610. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为 .
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(每题3分,共18分)
-
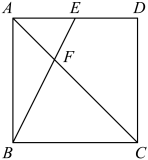
11. 如图,在正方形中,E为的中点,连接交于点F.若 , 则的面积为 .
 12. 如图四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数的图象经过第一象限点A,且平行四边形ABCD的面积为6,则 .
12. 如图四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数的图象经过第一象限点A,且平行四边形ABCD的面积为6,则 .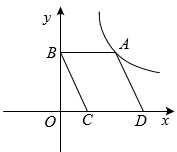 13. 如图,折叠边长为4cm的正方形纸片 , 折痕是 , 点落在点处,分别延长、交于点、 , 若点是边的中点,则cm.
13. 如图,折叠边长为4cm的正方形纸片 , 折痕是 , 点落在点处,分别延长、交于点、 , 若点是边的中点,则cm. 14. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).
14. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).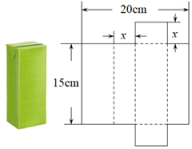 15. 如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=.
15. 如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=. 16. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .
16. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .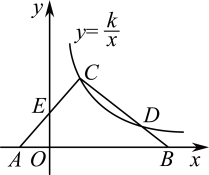
三、解答题(共8题,共72分)
-
17. 某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“良好”,“合格”,“不合格”.
 (1)、本次抽查总人数为 , “合格”人数的百分比为 .(2)、补全条形统计图.(3)、扇形统计图中“不合格人数”的度数为 .(4)、在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为 .18. 如图, 中, , 相交于点 , , 分别是 , 的中点.
(1)、本次抽查总人数为 , “合格”人数的百分比为 .(2)、补全条形统计图.(3)、扇形统计图中“不合格人数”的度数为 .(4)、在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为 .18. 如图, 中, , 相交于点 , , 分别是 , 的中点. (1)、求证: ;(2)、设 ,当 为何值时,四边形 是矩形?请说明理由.19. 列方程(组)解应用题
(1)、求证: ;(2)、设 ,当 为何值时,四边形 是矩形?请说明理由.19. 列方程(组)解应用题端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
20. 如图,正比例函数与反比例函数的图象交于 , 两点.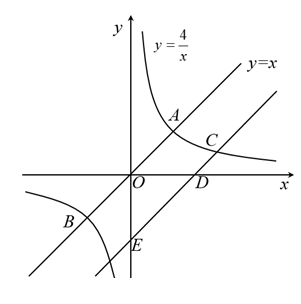 (1)、求 , 两点的坐标;(2)、将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点 , 与轴交于点 , 与轴交于点 , 若 , 求的值.21. 如图,四边形为菱形,点E在的延长线上, .
(1)、求 , 两点的坐标;(2)、将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点 , 与轴交于点 , 与轴交于点 , 若 , 求的值.21. 如图,四边形为菱形,点E在的延长线上, . (1)、求证:;(2)、当时,求的长.22. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)、求证:;(2)、当时,求的长.22. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.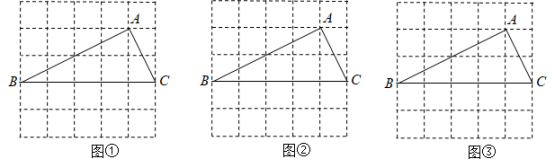 (1)、网格中的形状是;(2)、在图①中确定一点D,连结、 , 使与全等:(3)、在图②中的边上确定一点E,连结 , 使:(4)、在图③中的边上确定一点P,在边BC上确定一点Q,连结 , 使 , 且相似比为1:2.23. 在平面直角坐标系中,已知一次函数与坐标轴分别交于 , 两点,且与反比例函数的图象在第一象限内交于P,K两点,连接 , 的面积为 .
(1)、网格中的形状是;(2)、在图①中确定一点D,连结、 , 使与全等:(3)、在图②中的边上确定一点E,连结 , 使:(4)、在图③中的边上确定一点P,在边BC上确定一点Q,连结 , 使 , 且相似比为1:2.23. 在平面直角坐标系中,已知一次函数与坐标轴分别交于 , 两点,且与反比例函数的图象在第一象限内交于P,K两点,连接 , 的面积为 .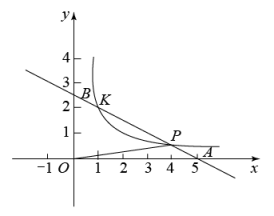 (1)、求一次函数与反比例函数的解析式;(2)、当时,求x的取值范围;(3)、若C为线段上的一个动点,当最小时,求的面积.24. 如图,在平行四边形中,是一条对角线,且 , , , 是边上两点,点在点的右侧, , 连接 , 的延长线与的延长线相交于点 .
(1)、求一次函数与反比例函数的解析式;(2)、当时,求x的取值范围;(3)、若C为线段上的一个动点,当最小时,求的面积.24. 如图,在平行四边形中,是一条对角线,且 , , , 是边上两点,点在点的右侧, , 连接 , 的延长线与的延长线相交于点 .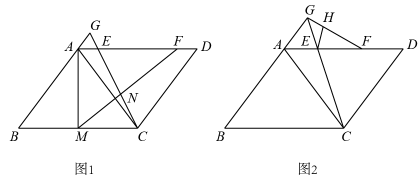 (1)、如图1,是边上一点,连接 , , 与相交于点 .
(1)、如图1,是边上一点,连接 , , 与相交于点 .①若 , 求的长;
②在满足①的条件下,若 , 求证:;
(2)、如图2,连接 , 是上一点,连接 . 若 , 且 , 求的长.