浙江省温州市苍南县2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-11-08 类型:期中考试
一、选择题(本题有10小题,每小题4分,共40分.)
-
1. 与“新冠肺炎”患者接触过程中, 下列哪种情况被传染的可能性最大( )A、戴口罩与患者近距离交谈 B、不戴口罩与患者近距离交谈 C、戴口罩与患者保持社交距离交谈 D、不戴口罩与患者保持社交距离交谈2. 已知的半径为 , 则点与的位置关系是( )A、点在圆外 B、点在圆上 C、点在圆内 D、不能确定3. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线4. 如图, 在中, , 则弧的度数为( )
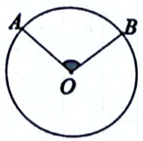 A、 B、 C、 D、5. 欢欢将自己的核酸检测二维码打印在面积为的正方形纸上, 如图所示, 为了估计图中黑色部分的面积, 他在纸内随机掷点, 经过大量重复试验, 发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的面积约为( )
A、 B、 C、 D、5. 欢欢将自己的核酸检测二维码打印在面积为的正方形纸上, 如图所示, 为了估计图中黑色部分的面积, 他在纸内随机掷点, 经过大量重复试验, 发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的面积约为( ) A、 B、 C、 D、6. 如图, 点的坐标为 , 点的坐标为的坐标为 , 将沿轴向下平移, 使点平移至坐标原点 , 再将绕点逆时针旋转 , 此时的对应点为 , 点的对应点为 , 则点的坐标为( )
A、 B、 C、 D、6. 如图, 点的坐标为 , 点的坐标为的坐标为 , 将沿轴向下平移, 使点平移至坐标原点 , 再将绕点逆时针旋转 , 此时的对应点为 , 点的对应点为 , 则点的坐标为( )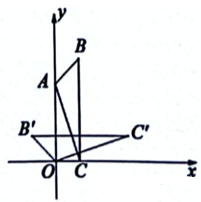 A、 B、 C、 D、7. 将拋物线先向左平移2个单位, 再向下平移1个单位, 得到的新拋物线必经过( )A、 B、 C、 D、8. 已知二次函数 , 当时, 对应的函数值不可能是( )A、-3 B、6 C、-2 D、79. 已知如图, 在正方形中, 点的坐标分别是 , 点在抛物线 的图像上, 则的值是( )
A、 B、 C、 D、7. 将拋物线先向左平移2个单位, 再向下平移1个单位, 得到的新拋物线必经过( )A、 B、 C、 D、8. 已知二次函数 , 当时, 对应的函数值不可能是( )A、-3 B、6 C、-2 D、79. 已知如图, 在正方形中, 点的坐标分别是 , 点在抛物线 的图像上, 则的值是( ) A、 B、 C、 D、10. 如图, 矩形中, 分别是边上的两个动点, 将沿着直线 作轴对称变换, 得到 , 点恰好在边上, 过点作 , 连结. 若时, 则( )
A、 B、 C、 D、10. 如图, 矩形中, 分别是边上的两个动点, 将沿着直线 作轴对称变换, 得到 , 点恰好在边上, 过点作 , 连结. 若时, 则( ) A、3 B、6 C、 D、
A、3 B、6 C、 D、二、 填空题(本题有6小题,每小题5分,共30分)
-
11. 抛物线的顶点坐标是.12. 已知每1000个盲盒中常规款有980个, “小隐藏” 15个, “大隐藏” 5个. 现随机抽取1盒, 抽取到的是“大隐藏”的概率为.13. 已知点和点是抛物线上的两点, 则的大小关系是ab (填 “>” 或 “<” 或 “=”).14. 如图,内接于是的直径,连结 , 若 , 则的半径.
 15. 如图, 在直角坐标系中, 抛物线交轴于点 , 点是点 关于对称轴的对称点, 点是抛物线的顶点, 若的外接圆经过原点 , 则点的坐标为.
15. 如图, 在直角坐标系中, 抛物线交轴于点 , 点是点 关于对称轴的对称点, 点是抛物线的顶点, 若的外接圆经过原点 , 则点的坐标为. 16. 图1是小米家吊椅的图片,其截面图如图2所示,吊椅的外框架是一条拋物线, 抛物线的最高点为点 , 内框架内由一条圆弧和两个全等直角三角形组成,点在同一条直线上. 已知 , 点和点的距离为 , 点 , 点到直线的距离分别为是等腰三角形,过点作 交于点 , 此时, , 则弧所在的圆的半径为.
16. 图1是小米家吊椅的图片,其截面图如图2所示,吊椅的外框架是一条拋物线, 抛物线的最高点为点 , 内框架内由一条圆弧和两个全等直角三角形组成,点在同一条直线上. 已知 , 点和点的距离为 , 点 , 点到直线的距离分别为是等腰三角形,过点作 交于点 , 此时, , 则弧所在的圆的半径为.
三、解答题(本题有 8 小题,共80分,)
-
17. 如图所示, 中, 弦与相交于点 , 连接 ,
 (1)、求证:(2)、求证: .18. 在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球. 其中红球3个, 白球5个, 黑球若干个, 若从中任意摸出一个白球的概率是.(1)、求任意摸出一个球是黑球的概率;(2)、小明从盒子里取出个白球 (其他颜色球的数量没有改变), 使得从盒子里任意摸出一个球是红球的概率为 , 请求出的值.19. 如图, 在的正方形网格中, 网线的交点称为格点, 点都是格点. 已知每个小正方形的边长为1 .
(1)、求证:(2)、求证: .18. 在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球. 其中红球3个, 白球5个, 黑球若干个, 若从中任意摸出一个白球的概率是.(1)、求任意摸出一个球是黑球的概率;(2)、小明从盒子里取出个白球 (其他颜色球的数量没有改变), 使得从盒子里任意摸出一个球是红球的概率为 , 请求出的值.19. 如图, 在的正方形网格中, 网线的交点称为格点, 点都是格点. 已知每个小正方形的边长为1 . (1)、画出的外接圆 , 直接写出的半径:(2)、连接 , 在网格中画出一个格点 , 使得是直角三角形,且点在上.20. 2022年冬奥会和残奥会的吉祥物 “冰墩墩” 和 “雪容融” 广受大众喜爱, 某校九年(1)班的迎新年班队课上, 老师在抽奖环节准备了四张奖券, 它们的形状外观大小完全一样, 已知四张奖券中有两张代表冬奥会吉祥物 “冰墩墩” 玩偶 (记作), 有一张代表残奥会吉样物“雪容融”玩偶 (记作),还有一张代表虎年特制的小老虎玩偶(记作).(1)、随机抽取一张奖券, 恰好代表 “冰墩墩” 玩偶的概率是.(2)、小丽同学在课堂上表现出色, 获得了两张奖券, 并且获得了优先抽奖资格。请利用树状图或列表法, 求小丽抽取的奖券恰好是一张“冰墩墩”玩偶和一张“雪容融”玩偶的概率.21. 如图, 抛物线为常数)的对称轴为直线 , 图象与轴交于和点 , 与轴的正半轴交于点 , 过点的直线 与轴交于点.
(1)、画出的外接圆 , 直接写出的半径:(2)、连接 , 在网格中画出一个格点 , 使得是直角三角形,且点在上.20. 2022年冬奥会和残奥会的吉祥物 “冰墩墩” 和 “雪容融” 广受大众喜爱, 某校九年(1)班的迎新年班队课上, 老师在抽奖环节准备了四张奖券, 它们的形状外观大小完全一样, 已知四张奖券中有两张代表冬奥会吉祥物 “冰墩墩” 玩偶 (记作), 有一张代表残奥会吉样物“雪容融”玩偶 (记作),还有一张代表虎年特制的小老虎玩偶(记作).(1)、随机抽取一张奖券, 恰好代表 “冰墩墩” 玩偶的概率是.(2)、小丽同学在课堂上表现出色, 获得了两张奖券, 并且获得了优先抽奖资格。请利用树状图或列表法, 求小丽抽取的奖券恰好是一张“冰墩墩”玩偶和一张“雪容融”玩偶的概率.21. 如图, 抛物线为常数)的对称轴为直线 , 图象与轴交于和点 , 与轴的正半轴交于点 , 过点的直线 与轴交于点. (1)、求抛物线的表达式, 并直接写出点的坐标;(2)、若点是抛物线上一动点, 过点作于点轴交直线于点 , 当时, 请求出点的坐标.22. 如图, 在中, , 点是边上一点, 以为直径的 经过点 , 点是直径上一点 (不与重合), 延长交圆于点 , 连接.
(1)、求抛物线的表达式, 并直接写出点的坐标;(2)、若点是抛物线上一动点, 过点作于点轴交直线于点 , 当时, 请求出点的坐标.22. 如图, 在中, , 点是边上一点, 以为直径的 经过点 , 点是直径上一点 (不与重合), 延长交圆于点 , 连接. (1)、求证: ;(2)、若 , 求的长.23. 在 “母亲节” 期间, 某校部分团员参加社会公益活动, 准备购进一批进价为6元/个的许愿瓶进行销售, 并将所得的利润捐给慈善机构. 根据市场调查, 这种许愿瓶每日的销售量(个)与销售单价(元/个)之间满足关系式: .(1)、求每日销售这种许愿瓶所得的利润(元)与销售单价之间的函数关系式.(2)、求每日销售这种许愿瓶所得的利润(元)的最大值及相应的销售单价.(3)、“国庆节” 期间, 该校公益团队想继续销售许愿瓶的慈善活动, 却发现批发商调整了许愿瓶的进货价格, 进价变为了元/个. 但是许愿瓶每日的销量与销售单价的关系不变. 为了不亏本, 至少需按照12元/个销售,而物价部门规定销售单价不得超过15元/个. 在实际销售过程中, 发现该商品每天获得的利润随的增大而增大, 求的最小值.24. 抛物线与轴交于点和 , 与轴交于点 , 连接. 点是线段下方抛物线上的一个动点(不与点重合), 过点作 轴的平行线交于 , 交轴于 , 设点的横坐标为.
(1)、求证: ;(2)、若 , 求的长.23. 在 “母亲节” 期间, 某校部分团员参加社会公益活动, 准备购进一批进价为6元/个的许愿瓶进行销售, 并将所得的利润捐给慈善机构. 根据市场调查, 这种许愿瓶每日的销售量(个)与销售单价(元/个)之间满足关系式: .(1)、求每日销售这种许愿瓶所得的利润(元)与销售单价之间的函数关系式.(2)、求每日销售这种许愿瓶所得的利润(元)的最大值及相应的销售单价.(3)、“国庆节” 期间, 该校公益团队想继续销售许愿瓶的慈善活动, 却发现批发商调整了许愿瓶的进货价格, 进价变为了元/个. 但是许愿瓶每日的销量与销售单价的关系不变. 为了不亏本, 至少需按照12元/个销售,而物价部门规定销售单价不得超过15元/个. 在实际销售过程中, 发现该商品每天获得的利润随的增大而增大, 求的最小值.24. 抛物线与轴交于点和 , 与轴交于点 , 连接. 点是线段下方抛物线上的一个动点(不与点重合), 过点作 轴的平行线交于 , 交轴于 , 设点的横坐标为. (1)、求该拋物线的解析式;(2)、用关于的代数式表示线段 , 求的最大值及此时点的坐标;(3)、过点作于点 ,
(1)、求该拋物线的解析式;(2)、用关于的代数式表示线段 , 求的最大值及此时点的坐标;(3)、过点作于点 ,①求点的坐标;
②连接 , 在轴上是否存在点 , 使得为直角三角形, 若存在,求出点的坐标; 若不存在,请说明理由.