浙江省金华市金东区2022-2023学年七年级上学期期中数学试题

试卷更新日期：2022-11-08 类型：期中考试

进入出卷网下载

一、选择题（本大题有10小题，每小题3分，共30分.）

1. 2022的相反数是（）

A、2022 B、-2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 一周时间有604800秒，604800用科学记数法表示为（）

A、 $6048 \times 10^{2}$ B、 $6.048 \times 10^{5}$ C、 $6.048 \times 10^{6}$ D、 $0.6048 \times 10^{6}$

查看试题解析
3. 下列表示数轴选项中，正确的是（）

A、 B、 C、 D、

查看试题解析
4. 下列数中，为无理数的是（）

A、 $\sqrt{5}$ B、-0.1 C、 $\frac{1}{2}$ D、-5

查看试题解析
5. 比-1小2的数是（）

A、-1 B、1 C、-3 D、3

查看试题解析
6. 已知 $- 5 x^{m} y^{3}$ 和 $9 x^{2} y^{n}$ 是同类项，则 $m - n$ 的值是（）

A、-1 B、-5 C、1 D、5

查看试题解析
7. 下列说法正确的是（）

A、4 的平方根是-2 B、8 的立方根是±2 C、任何实数都有平方根 D、任何实数都有立方根

查看试题解析
8. 下列说法中，正确的是（）

A、 $- \frac{2 a b}{3}$ 的系数是-2 B、 $3^{2} a b^{3}$ 的次数是6次 C、 $a^{2} + a - 1$ 的常数项是1 D、 $\frac{a + b}{3}$ 是多项式

查看试题解析
9. 若 $(- 12) \times 5 = p$ ，则 $(- 12) \times 6$ 的值可表示为（）.

A、 $p = 1$ B、 $p - 12$ C、 $p + 12$ D、 $\frac{5}{6} p$

查看试题解析
10. 任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和，如 $2^{3} = 3 + 5 ， 3^{3} = 7 + 9 + 11$ ， $4^{3} = 13 + 15 + 17 + 19 \dots \dots$ 仿此，若m³的“分裂数”中有一个是59，则m的值为（）

A、6 B、7 C、8 D、9

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 在知识抢答中，如果用＋10表示得10分，那么扣20分表示为.

查看试题解析
12. 在方程 $y + 2 x = 7$ 中，用 $y$ 来表示 $x$ ，则 $x =$ .

查看试题解析
13. 若 $\sqrt{a - 2} + | 3 - b | = 0$ ，则 $3 a + 2 b =$ ．

查看试题解析
14. 已知 $x^{2} + 3 x + 5$ 的值为3，则代数式 $2 x^{2} + 6 x - 1$ 的值为.

查看试题解析
15. 有一个数值转换器，其流程如图所示：

当输入 $x$ 的值是64时，则输出的 $y$ 值是.

查看试题解析
16. 已知有理数 $a ， b ， c$ 满足 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = 1$ ，则 $\frac{| a b c |}{a b c}$ 的值为．

查看试题解析

三、解答题（本大题有8小题，共66分）

17. 把下列各数对应的编号填在相应的大括号里：
（1） $- \sqrt{49}$ ，（2） $\sqrt{18}$ ，（3） $\frac{5}{7}$ ，（4） $\frac{π}{2}$ ，（5）—3.141，（6）0，（7）7，（8）80%，（9） $- | - 5 |$ ，（10）0.101001...（自左而右每两个1之间依次多一个0）.
整数：{                      ……}

分数：{                      ……}

无理数：{                       ……}

查看试题解析
18. 将-2，0， $| - \frac{1}{2} |$ ，在数轴上表示，并将原数用“<”连接.

查看试题解析
19. 先化简，再求值

(1)、 $(3 a^{2} - 7 a) + 2 (a^{2} - 3 a + 2)$ ，其中 $a = 1$ .

(2)、 $3 x y^{2} + (3 x^{2} y - 2 x y^{2}) - 4 (x y^{2} - x^{2} y)$ ，其中 $x = - 4 ， y = 1$ .

查看试题解析
20. 计算：

(1)、 $4 - (- 2) + (- 3)$

(2)、 $3^{2} \times (- \frac{1}{2}) \div \frac{3}{2}$

(3)、 $- \sqrt{9} + \sqrt[3]{64} - (- 1)^{3}$

(4)、 $(\frac{1}{4} - \frac{5}{6} + \frac{1}{2}) \times (- 12)$

查看试题解析

21. 某仓库原有某种货物库存270千克，现规定运入为正，运出为负，一天中七次出入如表（单位：千克）

第一次	第二次	第三次	第四次	第五次	第六次	第七次
-30	+82	-19	+102	-96	+34	-28

(1)、判断在第几次后库存量最大，说明相应理由.

(2)、求这一天最终库存量.

(3)、若运进货物与运出货物的装卸费都为每千克0.3元，问这一天装卸费需多少元？

查看试题解析

22. 如果规定△表示一种运算，且 $a Δ b = \frac{a - b}{a \times b}$ ，求下列运算的结果：

(1)、 $(- 3) Δ (+ 4)$

(2)、 $3 Δ [(- 3) Δ (- 1)]$

查看试题解析
23. 观察下列算式：
$1 + \frac{1}{3} = \frac{3 + 1}{3} = \frac{2^{2}}{1 \times 3}$ ；①

$1 + \frac{1}{8} = \frac{8 + 1}{8} = \frac{3^{2}}{2 \times 4}$ ；②

$1 + \frac{1}{15} = \frac{15 + 1}{15} = \frac{4^{2}}{3 \times 5}$ ；③

………按照上面的规律完成下列各题：

(1)、第④个算式： $1 + \frac{1}{24} = \frac{24 + 1}{24} =$ ；

(2)、第⑤个算式为；

(3)、第 n 个算式为；

(4)、计算： $(1 + \frac{1}{3}) \times (1 + \frac{1}{8}) \times (1 + \frac{1}{15}) \times \dots \times (1 + \frac{1}{99})$ .

查看试题解析
24. 数轴上，点 $A$ 表示的数为-7，点 $B$ 表示的数为-1，点 $C$ 表示的数为9，点 $D$ 表示的数为13，在点 $B$ 和点 $C$ 处各折一下，得到一条“折线数轴”如图所示，我们称点 $A$ 和点 $D$ 在数轴上相距20个长度单位，动点 $P$ 从点 $A$ 出发，沿着“折线数轴”的正方向运动，同时，动点 $Q$ 从点 $D$ 出发，沿着“折线数轴”的负方向运动，它们在“水平路线”射线 $B A$ 和射线 $C D$ 上的运动速度相同均为2个单位/秒，“上坡路段”从 $B$ 到 $C$ 速度变为“水平路线”速度的一半，“下坡路段”从 $C$ 到 $B$ 速度变为“水平路线”速度的2倍，设运动的时间为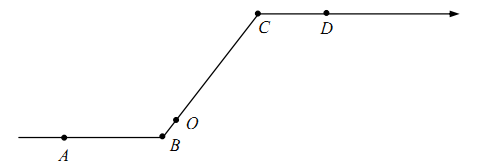 $t$ 秒，问：

(1)、求动点 $P$ 从点 $A$ 运动至 $D$ 点需要时间

(2)、求动点 $Q$ 运动到点 $O$ 时，点 $P$ 所在位置表示的数.

(3)、 $P ， Q$ 两点重合时，求运动时间 $t$ .

查看试题解析