浙江省温州十校联合体2022-2023学年高一上学期数学期中联考试卷
试卷更新日期:2022-11-08 类型:期中考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 命题“ , 都有”的否定是( )A、 , 都有 B、 , 使得 C、 , 使得 D、 , 使得3. , , , 则下列关于大小关系正确的是( )A、 B、 C、 D、4. 已知函数 , 则( )A、3 B、-3 C、-1 D、15. 已知 , 则“”是“关于x的一元二次方程没有实数根”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 已知函数的最小值为a,则函数的最小值为( )A、 B、 C、 D、7. 已知函数满足(其中),则函数的图象可能为( )A、
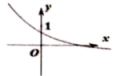 B、
B、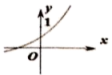 C、
C、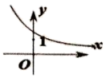 D、
D、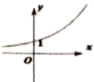 8. 已知函数是定义在上的单调函数,且对任意x,都有 , 则满足不等式的x的取值范围为( )A、 B、 C、 D、
8. 已知函数是定义在上的单调函数,且对任意x,都有 , 则满足不等式的x的取值范围为( )A、 B、 C、 D、二、多选题
-
9. 下列各组函数中,表示同一函数的是( )A、与 B、与 C、与 D、与10. 下列函数中,属于偶函数并且值域为的有( )A、 B、 C、 D、11. 下列说法正确的是( )A、函数在处取到最小值 B、函数的最小值是2 C、函数的最小值为 D、对任意 , 使得恒成立的a的最小值为12. 已知函数是定义在上的奇函数,当时,则下列结论正确的是( )A、函数与有2个交点 B、当时, C、在上单调递增 D、函数与有3个交点
三、填空题
-
13. 已知全集 , 集合 , , 则实数a的值为 .14. 函数的定义域为 .15. 中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关,经验表明,某种绿茶用85℃的开水泡制,再等茶水温度降至55℃时饮用,可以产生最佳口感,如果茶水原来的温度是℃,经过一定时间t min后的温度 (单位:℃)可由公式求得,其中表示室温,h是一个随着物体与空气的接触状况而定的正常数,现有一杯85℃的绿茶放在室温为25℃的房间中,如果茶温降到40℃需要20min.那么在25℃室温下,用85℃的开水刚泡好的茶水大约需要放置时间min,才能达到最佳饮用口感.16. 已知 , , 若存在实数 , 使得成立,则的取值范围为 .
四、解答题
-
17. 对下列式子化简求值(1)、求值:;(2)、已知(且),求的值.18. 已知集合 , .(1)、若 , 求;(2)、若_______,求实数的取值范围.
请从条件① , 条件② , 这两个条件中选一个填入(2)中横线处,并完成第(2)问的解答.
19. 已知函数 , 不等式的解集为 .(1)、求实数的值;(2)、若不等式对满足的所有实数都成立,求实数的取值范围.20. 已知函数是定义在R上的奇函数(其中实数).(1)、求实数m的值;(2)、试判断函数的单调性,并求不等式的解集.(无需证明单调性)21. 浙江正聚焦“富民、强村”以农村产业振兴为基础,实现乡村振兴乃至共同富裕.某乡镇以“共富果园”为目标,促进农业产业高质量发展,经调研发现,某特色果树的单接产量(单位:千克)与施用肥料(单位:千克)满足如下关系: , 另肥料成本投入为元,其它成本投入(如培育管理、施肥等人工费)为元.已知这种水果的市场售价大约为18元/千克,且销路畅通供不应求,记该水果树的单株利润为(单位:元).(1)、写出关于的函数解析式;(2)、当施用肥料为多少千克时,该果树的单株利润最大?最大利润是多少?22. 已知 .(1)、当时,解不等式;(2)、若 , 且函数的图像与直线有3个不同的交点,求实数a的取值范围.(3)、在(2)的条件下,假设3个交点的横坐标分别为 , , , 且 , 若恒成立,求实数t的取值范围.