浙江省宁波市海曙区2022-2023学年八年级上学期数学期中试卷
试卷更新日期：2022-11-08 类型：期中考试
一、选择题（共10小题，满分30分，每小题3分）
-
1. 剪纸是我国传统的民间艺术，它历史悠久，风格独特，深受国内外人士喜爱．下列剪纸作品中，为轴对称图形的是（ ）A、
B、
C、
D、
2. 以下列各组线段为边作三角形，可以构成直角三角形的是（ ）A、1，1，2 B、3，3，3 C、3，6，9 D、0.6，0.8，13. 等腰三角形的两边长分别为6和14，则这个三角形的周长为（ ）A、26 B、26或34 C、34 D、26或304. 下列各命题中，是假命题的是（ ）A、等腰三角形的两底角相等 B、全等三角形的对应边相等 C、若a2＝b2 ， 则a＝b D、若a2＞b2 ， 则|a|＞|b|5. 在△ABC和△A'B'C'中，AB＝A'B'，∠B＝∠B'，补充条件后，仍不一定能保证△ABC≌△A'B'C'，这个补充条件是（ ）A、BC＝B'C' B、∠A＝∠A' C、AC＝A'C' D、∠C＝∠C'6. 如图，在△ABC中，AB＝AC＝5，BC＝3，BD为中线，则△ABD与△BCD的周长之差为（ ）
A、1 B、2 C、3 D、47. 如图，用三角尺可按下面方法画角平分线：在已知的∠AOB 的两边上分别取点M、N，使OM＝ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（ ）
A、SSS B、SAS C、AAS D、HL8. 将一箱苹果分给若干个学生，每个学生都分到苹果。若每个学生分5个苹果，则还剩12个苹果；若每位学生分8个苹果，则有一个学生所分苹果不足8个．若学生的人数为x，则列式正确的是（ ）A、0≤5x+12-8（x-1）＜8 B、0＜5x+12-8（x-1）≤8 C、1≤5x+12-8（x-1）＜8 D、1＜5x+12-8（x-1）≤89. 勾股定理是人类最伟大的科学发现之一，在我国古算术《周髀算经》中早有记载．如图以直角三角形纸片的各边分别向外作正三角形纸片，再把较小的两张正三角形纸片按如图的方式放置在最大正三角形纸片内．若已知图中阴影部分的面积，则可知（ ）
A、直角三角形纸片的面积 B、最大正三角形纸片的面积 C、最大正三角形与直角三角形的纸片面积和 D、较小两个正三角形纸片重叠部分的面积10. 已知等边△ABC中，在射线BA上有一点D，连接CD，以CD为边向上作等边△CDE，连接BE和AE，下列结论：①AE＝BD；②AE与AB的所夹锐角为60°；③当D在线段AB或BA延长线上时，总有∠BED﹣∠AED＝2∠BDC；④∠BCD＝90°时，CE2+AD2＝AC2+DE2 ， 正确的结论序号有（ ）
A、①② B、①②③ C、①②④ D、①②③④二、填空题（共8小题，满分24分，每小题3分）
-
11. “对顶角相等”的逆命题是 ． （用“如果…那么…”的形式写出）12. 如图，△ABC中∠ABC＝∠ACB，AB的垂直平分线交AC于点D，若AB+BC＝10cm，则△DBC的周长为cm．
13. 如图，“人字梯”放在水平的地面上，AB＝AC，当梯子的一边与地面所夹的锐角α为60°时，两梯角之间的距离BC的长为2m．周日亮亮帮助妈妈整理换季衣服，先使α为60°，后又调整α为45°，则梯子顶端A离地面的高度下降了m．
14. 关于x的不等式组无解，则常数b的取值范围是 ．15. 等腰三角形一腰的中垂线与另一腰所在直线夹角为40°，该等腰三角形的底角的度数是.16. 如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE+EF的最小值为.
17. 在等腰 中， ，过点C作直线l∥AB，F是l上的一点，且 ，则 的度数为.18. 如图， ， 现用若干根等长的小棒从点A开始向右依次摆放，使小棒的两端恰好分别落在射线OB、OC上，其中AA1为第1根小棒，且OA＝AA1. 若恰好能摆放4根小棒，则θ 的取值范围是 ．
三、解答题（共6小题，满分46分）
-
19. 解下列不等式（组）：(1)、(2)、 .20. 如图，在6×6方格中，按下列要求画三角形，使它的顶点均在方格的顶点上（小正方形的边长为1）
（ 1 ）在图甲中画一个面积为8的等腰三角形；
（ 2 ）在图乙中画一个三角形与△ABC全等，且有一条公共边．
21. 如图，已知点P是等边△ABC内一点，连结PA，PB，PC，D为△ABC外一点，且∠DAP＝60°，连结DP，DC，AD＝DP．
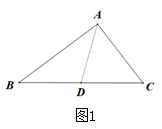
(1)、求证：△ADC≌△APB．(2)、若PA＝12，PB＝5，PC＝13，求∠APB的度数．22. 宁波市某中学为了教育学生，开展了以感恩为主题的有奖征文活动，并为获奖的同学颁发奖品．采购老师去商店购买甲、乙两种笔记本作为奖品，若买甲种笔记本20个，乙种笔记本10个，共用110元，且买甲种笔记本30个比买乙种笔记本20个少花10元．(1)、求甲、乙两种笔记本的单价各是多少元？(2)、若本次购进甲种笔记本的数量比乙种笔记本的数量的2倍还少10个，且购买这两种笔记本的总金额不超过320元，求本次乙种笔记本最多购买多少个？23. 如果一个三角形被一条线段分割成两个等腰三角形，那么这种分割叫做等腰分割，这条线段称为这个三角形的等腰分割线．如图1，当△ABD和△ACD为等腰三角形时，AD为△ABC的等腰分割线．
(1)、如图2，△ABC中，∠B＝2∠C，线段AC的垂直平分线ED交AC于点D，交BC于点E．求证：AE是△ABC的一条等腰分割线．
(2)、如图3，在△ABC中，∠A＝120°，∠B＝20°，∠C＝40°，请你用两种不同的方法完成△ABC的等腰分割，并在图中标注底角的度数．
(3)、在△ABC中，AD为△ABC的等腰分割线，且AD＝BD，∠C＝30°，请直接写出∠A的度数．24.(1)、【问题情境】课外兴趣小组活动时，老师提出了如下问题：如图1，在△ABC中，若AB＝13，AC＝9，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE＝AD，连接BE，容易证得△ADC≌△EDB，再由“三角形的三边关系”可求得AD的取值范围是 ．
解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．
(2)、【初步运用】如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且∠FAE＝∠AFE．若AE＝4，EC＝3，求线段BF的长．
(3)、【拓展提升】如图3，在△ABC中，D为BC的中点，DE⊥DF分别交AB，AC于点E，F．求证：BE+CF＞EF．