浙江省杭州市萧山区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-08 类型：期末考试

进入出卷网下载

一、单选题

1. $a - 2 a =$ （）

A、 $3 a$ B、 $a$ C、 $- a$ D、-2

查看试题解析
2. 根据浙江省统计局发布的最新数据，2021年前三季度杭州市GDP达到13151亿元，是前三季度全国14座GDP达到1万亿元的城市之一.数13151用科学记数法可以表示为（）

A、 ${1.3151}^{4}$ B、 $1.3151 \times 10^{4}$ C、 $0.13151 \times 10^{5}$ D、 $13151 \times 10^{8}$

查看试题解析
3. 下列运算，结果最小的是（）

A、 $1 - 2 + 3 - 4$ B、 $1 \times (- 2) + 3 - 4$ C、 $1 - (- 2 \times 3) - 4$ D、 $1 \times (- 2) \times 3 - 4$

查看试题解析
4. 如图，直线 $A C$ 、 $D E$ 交于点 $B$ ，则下列结论中一定成立的是（）

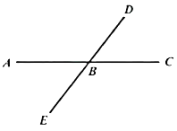A、 $∠ A B E + ∠ D B C = 180 °$ B、 $∠ A B E = ∠ D B C$ C、 $∠ A B D = ∠ A B E$ D、 $∠ A B D = 2 ∠ D B C$

查看试题解析
5. 4的平方根是（）

A、 ±2 B、2 C、﹣2 D、16

查看试题解析
6. 已知等式 $\frac{1}{3} a x = 4 a$ ，则下列等式中不一定成立的是（）

A、 $\frac{1}{3} a x - 4 a = 0$ B、 $\frac{1}{3} a x - b = 4 a - b$ C、 $a x = 12 a$ D、 $\frac{1}{3} x = 4$

查看试题解析
7. 已知，当 $x = 2$ 时， $a x^{3} + b x + c$ 的值是2022；当 $x = - 2$ 时， $a x^{3} + b x - c$ 的值是（）

A、-2022 B、-2018 C、2018 D、2022

查看试题解析
8. 程大位《直指算法统宗》：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁，意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分一个，正好分完．试问大、小和尚各多少人？设大和尚有x人，依题意列方程得（）

A、 $\frac{x}{3} - 3 (100 - x) = 100$ B、 $\frac{x}{3} + 3 (100 - x) = 100$ C、 $3 x - \frac{100 - x}{3} = 100$ D、 $3 x + \frac{100 - x}{3} = 100$

查看试题解析
9. 如图，∠AOB，以OA为边作∠AOC，使∠BOC= $\frac{1}{2}$ ∠AOB，则下列结论成立的是（）

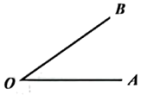A、 $∠ A O C = ∠ B O C$ B、 $∠ A O C < ∠ A O B$ C、 $∠ A O C = ∠ B O C$ 或 $∠ A O C = 2 ∠ B O C$ D、 $∠ A O C = ∠ B O C$ 或 $∠ A O C = 3 ∠ B O C$

查看试题解析
10. 图中的长方形 $A B C D$ 由1号、2号、3号、4号四个正方形和5号长方形组成，若1号正方形的边长为 $a$ ，3号正方形的边长为 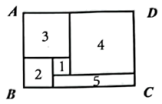$b$ ，则长方形 $A B C D$ 的周长为（）

A、 $16 a$ B、 $8 b$ C、 $4 a + 6 b$ D、 $8 a + 4 b$

查看试题解析

二、填空题

11. 单项式 $- 3 x^{2} y$ 的次数是.

查看试题解析
12. 如果一个角的补角是 $120 °$ ，那么这个角的度数是.

查看试题解析
13. 请用符号“ $<$ ”将下面实数 $- 3^{2}$ ， $\sqrt{3}$ ， $- 3$ 连接起来.

查看试题解析
14. 已知 $| x | = 6$ ， $y = - 2$ ，且 $| x - y | = x - y$ ，则 $x - y =$ .

查看试题解析
15. 定义一种新运算： $a \oplus b = a^{2} - 2 a b + b^{2}$ ，如 $1 \oplus 2 = 1^{2} - 2 \times 1 \times 2 + 2^{2} = 1$ ，若 $x \oplus (- 1) = x \oplus 3$ ，则 $x =$ .

查看试题解析
16. 如图，点 $A$ ， $B$ 是直线 $l$ 上的两点，点 $C$ ， $D$ 在直线 $l$ 上且点 $C$ 在点 $D$ 的左侧，点 $D$ 在点 $B$ 的右侧， $A C ： C B = 2 ： 1$ ， $B D ： A B = 3 ： 2$ .若 $C D = 11$ ，则 $A B =$ .

查看试题解析

三、解答题

17. 计算：

(1)、 $12 - (- 18) + (- 20) - 11$

(2)、 $- 6 \times (\frac{1}{2} - \frac{5}{3}) + \sqrt[3]{- 8}$

查看试题解析
18. 解方程：

(1)、 $7 - x = 3 x + 8$

(2)、 $\frac{2 x - 3}{10} = 1 + \frac{2 x + 1}{5}$

查看试题解析
19. 已知 $M = \frac{1}{2} (a b - 4 a^{2}) - 8 a b$ ， $N = 2 a (a - \frac{1}{4} b)$ ，求 $M + N$ 的值，其中 $a = - 1$ ， $b = \frac{1}{3}$ .

查看试题解析
20. 如图，直线 $C D$ ， $A B$ 相交于点 $O$ ， $∠ B O D$ 和 $∠ A O N$ 互余， $∠ A O N = ∠ C O M$ .

(1)、求 $∠ M O B$ 的度数；

(2)、若 $∠ C O M = \frac{1}{5} ∠ B O C$ ，求 $∠ B O D$ 的度数.

查看试题解析
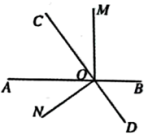21. 甲、乙两人分别从 $A$ ， $B$ 两地出发，甲骑自行车，乙骑摩托车，沿同一条路线相向匀速行驶.出发后经4小时两人在 $C$ 地相遇，相遇后经1小时乙到达 $A$ 地.

(1)、乙的行驶速度是甲的几倍？

(2)、若已知相遇时乙比甲多行驶了120公里，求甲、乙行驶的速度分别是多少？

查看试题解析
22. 在数学课上，老师给出了一道题目：“先化简再求值： $(x^{2} + □ x - 1) - 3 (\frac{1}{3} x^{2} - 2 x + 4)$ ，其中 $x = - 1$ ”， $□$ 中的数据被污染，无法解答，只记得 $□$ 中是一个实数，于是老师即兴出题，请同学们回答.

(1)、化简后的代数式中常数项是多少？

(2)、若点点同学把“ $x = - 1$ ”看成了“ $x = 1$ ”，化简求值的结果仍不变，求此时 $□$ 中数的值；

(3)、若圆圆同学把“ $x = - 1$ ”看成了“ $x = 1$ ”，化简求值的结果为-3，求当 $x = - 1$ 时，正确的代数式的值.

查看试题解析
23. 阅读材料：
材料1：如果一个四位数为 $\bar{a b c d}$ （表示千位数字为 $a$ ，百位数字为 $b$ ，十位数字为 $c$ ，个位数字为 $d$ 的四位数，其中 $a$ 为1~9的自然数， $b$ 、 $c$ 、 $d$ 为0~9的自然数），我们可以将其表示为： $\bar{a b c d} = 1000 a + 100 b + 10 c + d$ ；

材料2：把一个自然数（个位不为0）各位数字从个位到最高位倒序排列，得到一个新的数，我们称该数为原数的兄弟数，如数“123”的兄弟数为“321”.

(1)、四位数 $\bar{x 5 y 3} =$ ；（用含 $x$ ， $y$ 的代数式表示）

(2)、设有一个两位数 $\bar{x y}$ ，它的兄弟数与原数的差是45，请求出所有可能的数 $\bar{x y}$ ；

(3)、设有一个四位数 $\bar{a b c d}$ 存在兄弟数，且 $a + d = b + c$ ，记该四位数与它的兄弟数的和为 $S$ ，问 $S$ 能否被1111整除？试说明理由.

查看试题解析