浙江省杭州拱墅区2021-2022学年七年级上学期期末考试数学试题
试卷更新日期:2022-11-08 类型:期末考试
一、单选题
-
1. 下列各数中,是负整数的是( )A、+1 B、-2 C、 D、02. 把34.75精确到个位得到的近似数是( )A、30 B、34.8 C、34 D、353. 下列等式成立的是( )A、 B、 C、 D、4. 计算下列各式,值为负数的是( )A、 B、 C、 D、5. 如图,实数在数轴上的对应点可能是( )
 A、点 B、点 C、点 D、点6. 几人共同种一批树苗,如果每人种10棵,则剩下6棵树苗未种;如果每人种12棵,则缺8棵树苗.设参与种树苗的有人,则( )A、 B、 C、 D、7. 如图,点 , 点都在线段上,若 , 则( )
A、点 B、点 C、点 D、点6. 几人共同种一批树苗,如果每人种10棵,则剩下6棵树苗未种;如果每人种12棵,则缺8棵树苗.设参与种树苗的有人,则( )A、 B、 C、 D、7. 如图,点 , 点都在线段上,若 , 则( ) A、 B、 C、 D、8. 观察下列按一定规律排列的个数:1,3,5,7,9,…,若最后三个数之和是99,则这列数中最大的数为( )A、17 B、19 C、33 D、359. 当为1,2,4时,代数式的值分别是 , 1, , 则的值为( )A、4 B、3 C、2 D、110. 如图,点在直线上,射线 , 在直线的同一侧(其中 , ),射线平分 , 射线平分 . 若和互补,则( )
A、 B、 C、 D、8. 观察下列按一定规律排列的个数:1,3,5,7,9,…,若最后三个数之和是99,则这列数中最大的数为( )A、17 B、19 C、33 D、359. 当为1,2,4时,代数式的值分别是 , 1, , 则的值为( )A、4 B、3 C、2 D、110. 如图,点在直线上,射线 , 在直线的同一侧(其中 , ),射线平分 , 射线平分 . 若和互补,则( )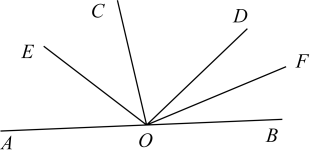 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 2的相反数是 , -3的绝对值是 .12. 计算: .13. 计算: .14. 若实数满足 , 则2(填“>”或“<”).15. 已知-2是关于的方程的解,则的值为 .16. 如图,点是线段的中点,点是线段的中点,点是线段的中点,点是线段的中点.若 , 则;若 , 则(用含的代数式表示).

三、解答题
-
17. 计算:(1)、 .(2)、 .18. 解方程:(1)、 .(2)、 .19. 先化简,再求值:(1)、 , 其中 .(2)、 , 其中 , .20. 下图是一个运算程序示意图:
 (1)、若输入的数 , 求输出的数值的值.(2)、若输出的数值 , 求输入的数的值.21. 一辆客车和一辆卡车都从地出发沿同一条公路匀速驶向地,客车的行驶速度为70千米/小时,卡车的行驶速度为60千米/小时,已知卡车提前1小时出发,结果两车同时到达地.(1)、求 , 两地的距离是多少?(2)、客车出发多少小时后,两车第一次相距20千米?22. 已知 , 过点作射线 , 射线平分 .(1)、如图1,射线在的外部(),
(1)、若输入的数 , 求输出的数值的值.(2)、若输出的数值 , 求输入的数的值.21. 一辆客车和一辆卡车都从地出发沿同一条公路匀速驶向地,客车的行驶速度为70千米/小时,卡车的行驶速度为60千米/小时,已知卡车提前1小时出发,结果两车同时到达地.(1)、求 , 两地的距离是多少?(2)、客车出发多少小时后,两车第一次相距20千米?22. 已知 , 过点作射线 , 射线平分 .(1)、如图1,射线在的外部(),
①若 , 求的度数.
②若 , 求的度数.
(2)、如图2,射线在的内部(),若存在射线(),使得 , 试求出与之间的等量关系. 23. 将长方形Ⅰ,正方形Ⅱ,正方形Ⅲ,以及长方形Ⅳ,按如图所示放入长方形中(相邻的长方形,正方形之间既无重叠,又无空隙),已知(为常数), .
23. 将长方形Ⅰ,正方形Ⅱ,正方形Ⅲ,以及长方形Ⅳ,按如图所示放入长方形中(相邻的长方形,正方形之间既无重叠,又无空隙),已知(为常数), . (1)、若 .
(1)、若 .①求 , 的长(用含的代数式表示).
②若长方形Ⅰ的周长是正方形Ⅲ的周长的倍,求的值.
(2)、若已知大长方形的周长为12,则能否求出正方形Ⅱ,以及长方形Ⅳ的周长?若能,请求出相应的周长;若不能,请说明理由.