内蒙古自治区通辽经济技术开发区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 下列事件中是必然事件的为( )A、三点确定一个圆 B、抛掷一枚骰子,朝上的一面点数恰好是5 C、四边形有一个外接圆 D、圆的切线垂直于过切点的半径2. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 如图,正方形 内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为( )
 A、 B、 C、 D、4. 如图,等边三角形的边长为8,以上一点O为圆心的圆分别与边 , 相切,则的半径为( )
A、 B、 C、 D、4. 如图,等边三角形的边长为8,以上一点O为圆心的圆分别与边 , 相切,则的半径为( )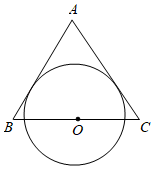 A、 B、3 C、4 D、5. 由二次函数y=2(x-3)2+1,可知( )A、其图象的开口向下 B、其图象的顶点坐标为(3,1) C、其图象的对称轴为直线x=-3 D、当x<3时,y随x的增大而增大6. 如图,在△ABC中,∠ACB=90°,∠A=20°,将△ABC绕点C按逆时针方向旋转角α到△A′B′C的位置,其中A′、B′分别是A、B的对应点,B在A′B′上,CA′交AB于D,则∠ACD的度数为( )
A、 B、3 C、4 D、5. 由二次函数y=2(x-3)2+1,可知( )A、其图象的开口向下 B、其图象的顶点坐标为(3,1) C、其图象的对称轴为直线x=-3 D、当x<3时,y随x的增大而增大6. 如图,在△ABC中,∠ACB=90°,∠A=20°,将△ABC绕点C按逆时针方向旋转角α到△A′B′C的位置,其中A′、B′分别是A、B的对应点,B在A′B′上,CA′交AB于D,则∠ACD的度数为( )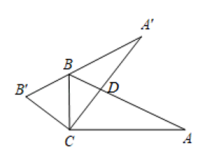 A、40° B、45° C、50° D、60°7. 将抛物线y=-3x2+1向左平移2个单位长度,再向下平移1个单位长度,所得的抛物线解析式为( )A、y=-3(x+2)2 B、y=-3(x-2)2-1 C、y=-3(x+1)2-1 D、y=-3(x-1)2+38. 如图, 分别与 相切于 两点, ,则 ( )
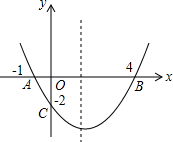
A、40° B、45° C、50° D、60°7. 将抛物线y=-3x2+1向左平移2个单位长度,再向下平移1个单位长度,所得的抛物线解析式为( )A、y=-3(x+2)2 B、y=-3(x-2)2-1 C、y=-3(x+1)2-1 D、y=-3(x-1)2+38. 如图, 分别与 相切于 两点, ,则 ( )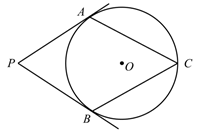 A、 B、 C、 D、9. 关于x的方程kx2+4x+4=0有实数根,则k的取值范围是( )A、k<1 B、k<1且k≠0 C、k≤1 D、k≤1且k≠010. 二次函数 的图象如图所示,对称轴是直线 .下列结论:① ;② ;③ ;④ ( 为实数).其中结论正确的个数为( )
A、 B、 C、 D、9. 关于x的方程kx2+4x+4=0有实数根,则k的取值范围是( )A、k<1 B、k<1且k≠0 C、k≤1 D、k≤1且k≠010. 二次函数 的图象如图所示,对称轴是直线 .下列结论:① ;② ;③ ;④ ( 为实数).其中结论正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 今年“国庆节”和“中秋节”双节期间,某微信群规定,群内的每个人都要发一个红包,并保证群内其他人都能抢到且自己不能抢自己发的红包,若此次抢红包活动,群内所有人共收到90个红包,则该群一共有人.12. 用半径为9,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径等于 .13. 已知关于x的方程x2-6x+k=0的一个解是x=2,则方程的另一个解是 .14. 如图是抛物线的一部分,其对称轴为直线 , 若其与x轴一交点为 , 则由图象可知,不等式的解集是 .
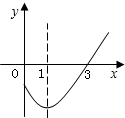 15. 如图,将等边△AOB放在平面直角坐标系中,点A的坐标为 ,点B在第一象限,将等边△AOB绕点O顺时针旋转180°得到△A′OB′,则点B′的坐标是 .
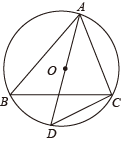
15. 如图,将等边△AOB放在平面直角坐标系中,点A的坐标为 ,点B在第一象限,将等边△AOB绕点O顺时针旋转180°得到△A′OB′,则点B′的坐标是 .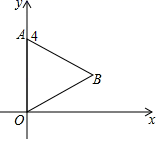 16. 已知一个直角三角形的两条直角边分别是6和8,则此直角三解形的内切圆半径r=.17. 如图,AB,AC分别是☉O的直径和弦,OD⊥AC于点D,连接BD,BC,AB=5,AC=4,则BD=.
16. 已知一个直角三角形的两条直角边分别是6和8,则此直角三解形的内切圆半径r=.17. 如图,AB,AC分别是☉O的直径和弦,OD⊥AC于点D,连接BD,BC,AB=5,AC=4,则BD=.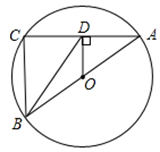
三、解答题
-
18. 用适当的方法解下列方程:(1)、x-3=x(x-3)(2)、3x2-5x=219. 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(−2,1),B(−4,1),C(−2,4).
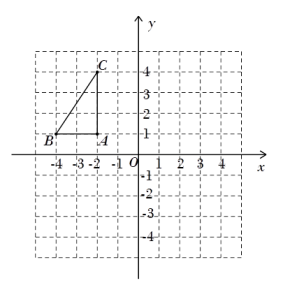
( 1 )画出△ABC关于y轴对称的△;
( 2 )将△ABC绕点B顺时针旋转90°后得到△A2B2C2 , 并求出线段BC在旋转过程中所扫过的面积.(结果保留π)
20. 如图,有一农户要建一个矩形鸡舍,鸡舍的一边利用长为a米的墙,另外三边用25米长的篱笆围成,为方便进出,在垂直于墙的一边CD上留一个1米宽的门,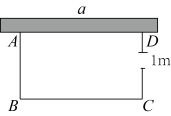 (1)、若a=12,问矩形的边长分别为多少时,鸡舍面积为80平方米(2)、若住房墙的长度足够长,问鸡舍面积能否达到90平方米?21. 已知二次函数y=x2-2x-3
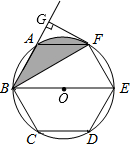
(1)、若a=12,问矩形的边长分别为多少时,鸡舍面积为80平方米(2)、若住房墙的长度足够长,问鸡舍面积能否达到90平方米?21. 已知二次函数y=x2-2x-3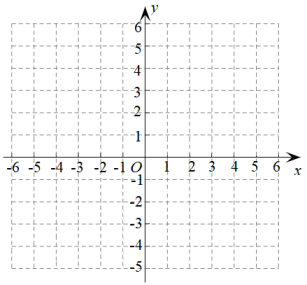 (1)、图象的开口方向 ,顶点坐标;(2)、图象与x轴的交点坐标 ,图象与y轴的交点坐标;(3)、在直角坐标系中,画出它的图象;22. 如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如图EM经过圆心交⊙O于点E,EM⊥CD,并且CD=4cm,EM=6cm,求⊙O的半径.
(1)、图象的开口方向 ,顶点坐标;(2)、图象与x轴的交点坐标 ,图象与y轴的交点坐标;(3)、在直角坐标系中,画出它的图象;22. 如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如图EM经过圆心交⊙O于点E,EM⊥CD,并且CD=4cm,EM=6cm,求⊙O的半径.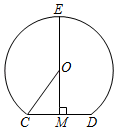 23. A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.求两次传球后,球恰在B手中的概率.
23. A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.求两次传球后,球恰在B手中的概率.