内蒙古自治区呼伦贝尔市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 下面这些图案中既是轴对称图形又是中心对称图形的是( )A、
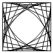 B、
B、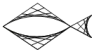 C、
C、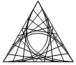 D、
D、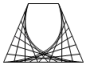 2. 在-3,-2,1,2,3五个数中随机选取一个数作为二次函数中a的值,则该二次函数图象开口向上的概率是( )A、 B、 C、 D、3. 在平面直角坐标系中,点A(2,3)关于原点对称的点的坐标是( )A、(2,3) B、(-2,3) C、(-3,-2) D、(-2,-3)4. 关于x的方程 是一元二次方程,则m的值为( )A、-2 B、2 C、±2 D、15. 下列语句中正确的有( )
2. 在-3,-2,1,2,3五个数中随机选取一个数作为二次函数中a的值,则该二次函数图象开口向上的概率是( )A、 B、 C、 D、3. 在平面直角坐标系中,点A(2,3)关于原点对称的点的坐标是( )A、(2,3) B、(-2,3) C、(-3,-2) D、(-2,-3)4. 关于x的方程 是一元二次方程,则m的值为( )A、-2 B、2 C、±2 D、15. 下列语句中正确的有( )①相等的圆心角所对的弧相等; ②平分弦的直径垂直于弦;
③三点确定一个圆; ④ 经过圆心的每一条直线都是圆的对称轴.
A、1个 B、2个 C、3个 D、4个6. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( ) A、 B、 C、 D、7. 如图,电路图上有 个开关 、 、 、 和 个小灯泡,同时闭合开关 、 或同时闭合开关 、 都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )
A、 B、 C、 D、7. 如图,电路图上有 个开关 、 、 、 和 个小灯泡,同时闭合开关 、 或同时闭合开关 、 都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )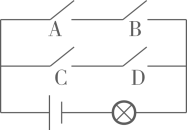 A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关8. 若点A(-2,y1),B(1,y2),C(3,y3)在二次函数图象上,则y1 , y2 , y3的大小关系是( )(用“<”连接)A、y3<y2<y1 B、y1<y2<y3 C、y2<y1<y3 D、y2<y3<y19. 如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,点D是劣弧上的一点,则∠ADB=( )
A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关8. 若点A(-2,y1),B(1,y2),C(3,y3)在二次函数图象上,则y1 , y2 , y3的大小关系是( )(用“<”连接)A、y3<y2<y1 B、y1<y2<y3 C、y2<y1<y3 D、y2<y3<y19. 如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,点D是劣弧上的一点,则∠ADB=( )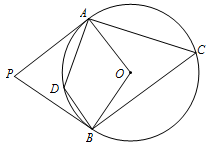 A、108° B、72° C、54° D、126°10. 某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循环形式(每两班之间都赛一场),共需安排36场比赛,则八年级班级的个数为( )A、6 B、9 C、7 D、811. 二次函数 的图象如图所示,有如下结论:① ;② ;③ ;④ (m为实数).其中正确结论的个数是( )
A、108° B、72° C、54° D、126°10. 某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循环形式(每两班之间都赛一场),共需安排36场比赛,则八年级班级的个数为( )A、6 B、9 C、7 D、811. 二次函数 的图象如图所示,有如下结论:① ;② ;③ ;④ (m为实数).其中正确结论的个数是( )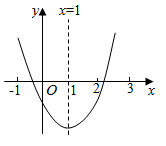 A、1个 B、2个 C、3个 D、4个12. 如图,在 中, , , 于点D.点 从点A出发,沿 的路径运动,运动到点C停止,过点 作 于点E,作 于点F.设点P运动的路程为x,四边形 的面积为y,则能反映y与x之间函数关系的图象是( )
A、1个 B、2个 C、3个 D、4个12. 如图,在 中, , , 于点D.点 从点A出发,沿 的路径运动,运动到点C停止,过点 作 于点E,作 于点F.设点P运动的路程为x,四边形 的面积为y,则能反映y与x之间函数关系的图象是( ) A、
A、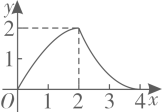 B、
B、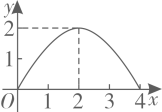 C、
C、 D、
D、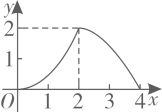
二、填空题
-
13. 把抛物线y=2(x-1)2+1向左平移1个单位,再向上平移2个单位得到的抛物线解析式 .14. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 .
 15. 如图,在拧开一个边长为a的正六角形螺帽时,扳手张开的开口b=20mm,则边长a为mm.
15. 如图,在拧开一个边长为a的正六角形螺帽时,扳手张开的开口b=20mm,则边长a为mm.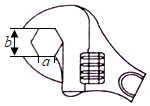 16. 如图,从一块直径是m的圆形铁皮上剪出一个圆心角为90°的扇形,将其围成一个圆锥,圆锥底面圆的半径是m.
16. 如图,从一块直径是m的圆形铁皮上剪出一个圆心角为90°的扇形,将其围成一个圆锥,圆锥底面圆的半径是m. 17. 已知点P( , )和直线 , 求点P到直线的距离d可用公式计算.根据以上材料解决下面问题:如图,⊙C的圆心C的坐标为(1,1),半径为1,直线AB的表达式为 , P是直线AB上的动点,Q是⊙C上的动点,则PQ的最小值是 .
17. 已知点P( , )和直线 , 求点P到直线的距离d可用公式计算.根据以上材料解决下面问题:如图,⊙C的圆心C的坐标为(1,1),半径为1,直线AB的表达式为 , P是直线AB上的动点,Q是⊙C上的动点,则PQ的最小值是 .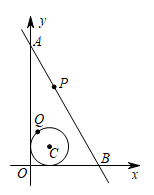
三、解答题
-
18. 解方程:19. 已知:关于x的一元二次方程有两个不相等的实数根,求m的正整数解.20. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内, △ABO的三个顶点坐标分别为A(-1,3),B(-4,3),O(0,0).
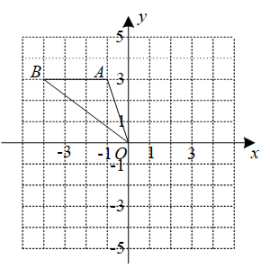 (1)、画出△ABO绕点O顺时针旋转90°后得到的△A1B1O;(2)、在(1)的条件下,求点A旋转到点A1所经过的路径长(结果保留π).21. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BE,
(1)、画出△ABO绕点O顺时针旋转90°后得到的△A1B1O;(2)、在(1)的条件下,求点A旋转到点A1所经过的路径长(结果保留π).21. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BE,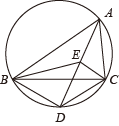 (1)、若∠CBD=34°,求∠BEC的度数;(2)、求证:DE=DB.22. 如图1,D是等边三角形ABC内部的一点,连接DA,DB,DC.将△BCD绕着点C顺时针旋转一定的角度得到△ACE,连接DE.
(1)、若∠CBD=34°,求∠BEC的度数;(2)、求证:DE=DB.22. 如图1,D是等边三角形ABC内部的一点,连接DA,DB,DC.将△BCD绕着点C顺时针旋转一定的角度得到△ACE,连接DE.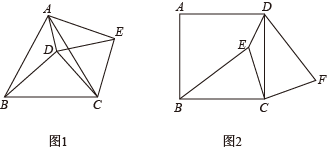 (1)、图1中,若AD=3,CD=4,BD=5,求∠ADC的度数;(2)、如图2,E为正方形ABCD内部的一点,连接EB,EC,ED,将△BCE绕着点C顺时针旋转一定的角度得到△DCF.若∠DEC=135°,DE=2,CE=4,则BE的长为 .23. 疫情期间,某市积极开展“停课不停学”线上教学活动,某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为:A.效果良好;B.效果较好;C.效果一般;D.效果不理想)并根据调查结果绘制了如下两幅不完整的统计图:
(1)、图1中,若AD=3,CD=4,BD=5,求∠ADC的度数;(2)、如图2,E为正方形ABCD内部的一点,连接EB,EC,ED,将△BCE绕着点C顺时针旋转一定的角度得到△DCF.若∠DEC=135°,DE=2,CE=4,则BE的长为 .23. 疫情期间,某市积极开展“停课不停学”线上教学活动,某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为:A.效果良好;B.效果较好;C.效果一般;D.效果不理想)并根据调查结果绘制了如下两幅不完整的统计图: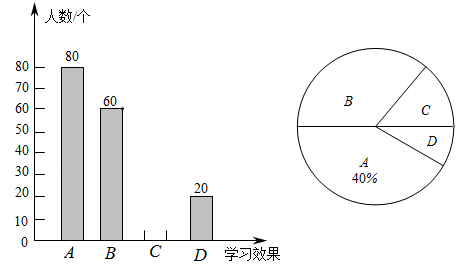 (1)、此次调查中,共抽查了名学生;(2)、补全条形统计图,扇形统计图中“效果一般”对应的圆心角为 °;(3)、某班4人学习小组,甲、乙2人认为效果良好,丙认为效果较好,丁认为效果一般.从学习小组中随机抽取2人,则“1人认为效果良好,1人认为效果较好”的概率是多少?(要求列表或画树状图求概率)24. 如图,在 ▱ ABCD中,∠D=60°,对角线AC⊥BC,⊙O经过点A,B,与AC交于点M,连接AO并延长与⊙O交于点F,与CB的延长线交于点E,AB=EB.
(1)、此次调查中,共抽查了名学生;(2)、补全条形统计图,扇形统计图中“效果一般”对应的圆心角为 °;(3)、某班4人学习小组,甲、乙2人认为效果良好,丙认为效果较好,丁认为效果一般.从学习小组中随机抽取2人,则“1人认为效果良好,1人认为效果较好”的概率是多少?(要求列表或画树状图求概率)24. 如图,在 ▱ ABCD中,∠D=60°,对角线AC⊥BC,⊙O经过点A,B,与AC交于点M,连接AO并延长与⊙O交于点F,与CB的延长线交于点E,AB=EB.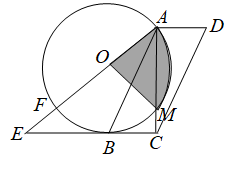 (1)、求证:EC是⊙O的切线;(2)、若AD=2 , 求扇形OAM的面积(结果保留π).25. 某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,如调整价格,每上涨1元,每天的销售量就减少10件.(1)、请写出商场销售这种文具,每天所得的销售利润w(元)与销售价格之间的函数关系式;(2)、销售价格为多少元时,该文具的销售利润最大?(3)、商场的营销部结合上述情况,提出了A,B两种营销方案.
(1)、求证:EC是⊙O的切线;(2)、若AD=2 , 求扇形OAM的面积(结果保留π).25. 某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,如调整价格,每上涨1元,每天的销售量就减少10件.(1)、请写出商场销售这种文具,每天所得的销售利润w(元)与销售价格之间的函数关系式;(2)、销售价格为多少元时,该文具的销售利润最大?(3)、商场的营销部结合上述情况,提出了A,B两种营销方案.方案A:该文具的销售价格高于进价且不超过30元/件;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.请通过计算说明哪种方案的最大利润更高.
26. 如图所示,抛物线(a≠0)与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(-2,0),点C的坐标为(0,6),对称轴为直线x=1.点D是抛物线上的一个动点,设点D的横坐标为m(1<m<4),连接AC,BC,DC,DB.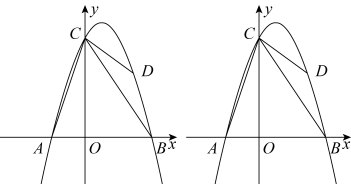 (1)、求抛物线的函数解析式;(2)、当△BCD的面积等于△AOC的面积的时,求m的值;(3)、在(2)的条件下,若点M是x轴上的动点,点N是抛物线上的动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,求出点M的坐标;若不存在,请说明理由.
(1)、求抛物线的函数解析式;(2)、当△BCD的面积等于△AOC的面积的时,求m的值;(3)、在(2)的条件下,若点M是x轴上的动点,点N是抛物线上的动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,求出点M的坐标;若不存在,请说明理由.