内蒙古自治区呼和浩特市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1. 一只不透明的袋子里装有4个黑球，1个白球，每个球除颜色外都相同，则从中任意摸出1个球，摸到黑球的概率是（）

A、0.8 B、0.4 C、0.2 D、0.1

查看试题解析
2. 下列方程中，无实数根的方程是（）

A、 $x^{2} + 3 x = 0$ B、 $x^{2} + 2 x - 1 = 0$ C、 $x^{2} + 2 x + 1 = 0$ D、 $x^{2} - x + 3 = 0$

查看试题解析
3. 下列事件中，必然事件是（）

A、姚明在罚球线上投篮一次，投中 B、掷一枚质地均匀的骰子，出现的数字小于7 C、任意画一个三角形，其内角和是360度 D、经过有交通信号灯的路口，遇到红灯

查看试题解析
4. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
5. 直径为10分米的圆柱形排水管，截面如图所示．若管内有积水（阴影部分），水面宽AB为8分米，则积水的最大深度CD为（）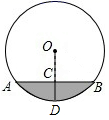

A、2分米 B、3分米 C、4分米 D、5分米

查看试题解析
6. 将抛物线 $y = 2 {(x - 3)}^{2} + 2$ 向左平移3个单位长度，再向下平移2个单位长度，得到抛物线的解析式是（）

A、 $y = 2 {(x - 6)}^{2}$ B、 $y = 2 {(x - 6)}^{2} + 4$ C、 $y = 2 x^{2}$ D、 $y = 2 x^{2} + 4$

查看试题解析
7. 在数轴上，点A所表示实数为5，点B所表示实数为a，⊙A半径为3.下列说法中错误的是（）

A、当a＞8时，点B在⊙A外 B、当a＜8时，点B在⊙A内 C、当a＜2时，点B在⊙A外 D、当2＜a＜8时，点B在⊙A内

查看试题解析
8. 关于二次函数y＝2x²＋4x-1，下列说法正确的是（）

A、图象与y轴的交点坐标为（0，1） B、当x＜1时，y的值随x值的增大而减小 C、图象的顶点坐标为（-1，-3） D、图象的对称轴在y轴的右侧

查看试题解析
9. 如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠CDA＝118°，则∠C的度数为（）

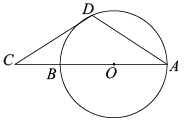A、32° B、33° C、34° D、44°

查看试题解析
10. 已知函数：y $= - \sqrt{x^{3} - \frac{2}{x}}$ ，则下列关于此函数的图象与性质描述正确的是（）

A、图象与x轴有两个交点，与y轴有一个交点 B、图象关于原点中心对称 C、图象不经过第一象限 D、x＞0时，y随x的增大而减小

查看试题解析

二、填空题

11. 若正六边形的周长是24，则它的外接圆半径是．

查看试题解析
12. 二次函数y＝（x＋1）²-3最小值为．

查看试题解析
13. 如图，PA，PB是⊙O的两条切线，A，B为切点，若OA＝2，∠APB＝60°，则PB＝．

查看试题解析
14. 抛物线y＝ax²＋bx＋c（a＞0）与x轴的两个交点分别是A（-1，0），B（2，0）．当y＞0时，x的取值范围是．

查看试题解析
15. 利用因式分解法可以将一元二次方程x（x-2）＋x-2＝0转化为两个一元一次方程求解，这两个一元一次方程分别为．

查看试题解析
16. 如图，四边形ABCD内接于⊙O，F是 $\overset{⌢}{CD}$ 上一点，且 $\overset{⌢}{DF} = \overset{⌢}{BC}$ ，连接CF并延长交AD的延长线于点E，连接AC.若∠ABC＝105°，∠BAC＝25°，则∠E的度数为度.

查看试题解析
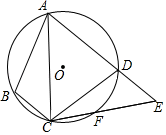17. 已知圆锥的底面半径为6，母线长为10，则此圆锥的侧面积为.

查看试题解析
18. 已知二次函数y＝x²-2bx＋c（b≠0），则自变量b＋1与b-1分别对应的函数值y₁与y₂的大小关系为．

查看试题解析

三、解答题

19. 解方程：

(1)、x²＋2x-2＝0；

(2)、（x-2）²＝（2x-1）（x-2）．

查看试题解析
20. 在如图的方格中，每个小正方形的边长都为1，△ABC的顶点均在格点上．在建立平面直角坐标系后，点B的坐标为（-1，2）．
( 1 )把△ABC向下平移8个单位后得到对应的△A₁B₁C₁ ，画出△A₁B₁C₁ ，并写出A₁坐标．
( 2 )以原点O为对称中心，画出与△A₁B₁C₁关于原点O对称的△A₂B₂C₂ ，并写出点B₂的坐标．

查看试题解析
21. 假定鸟卵孵化后，雏鸟为雌鸟和雄鸟的概率相同，如果三枚鸟卵全部成功孵化，用列举法求出三只雏鸟中恰有两只雄鸟的概率．

查看试题解析
22. 已知关于x的一元二次方程 $x^{2} + 4 x + 2 k = 0$ 有两个不相等的实数根x₁ ， x₂

(1)、求k的取值范围；

(2)、若 $x_{1}^{2} + x_{2}^{2} = k^{2} + 2 k$ ，求出k的值．

查看试题解析
23. 如图，一名男生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是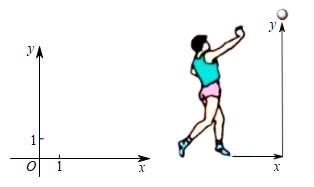 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$

(1)、在给出的平面直角坐标系中画出上述函数的大致图象；

(2)、求铅球推出的距离；

(3)、根据函数图象中的某些点可以大致估计该男生的身高，请你写出你选择的点的坐标及对身高的估计．

查看试题解析
24. 如图，已知圆内接四边形ABCD，AB∥DC．

(1)、求证：AD＝BC；

(2)、当圆内接四边形ABCD的对角线AC与BD交于圆心O时，判断四边形ABCD的形状，并写出判断过程．

查看试题解析
25. 如图①，在矩形ABCD中，AB＝6，BC＝8，四边形EFGH是正方形，EH与BD重合，将图①中的正方形EFGH绕着点D逆时针旋转．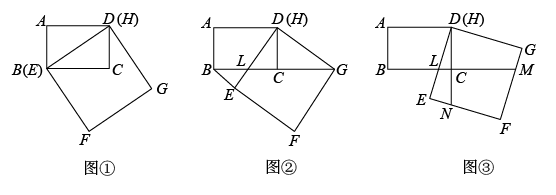

(1)、旋转至如图②位置，使点G落在BC的延长线上，DE交BC于点L．已知旋转开始时，即图①位置∠CDG＝37°，求正方形EFGH从图①位置旋转至图②位置时，旋转角的度数．

(2)、旋转至如图③位置，DE交BC于点L．延长BC交FG于点M，延长DC交EF于点N．试判断DL、EN、GM之间满足的数量关系，并给予证明．

查看试题解析
26. 在平面直角坐标系xOy中，二次函数y=ax²-2ax+c的图象经过点A（-1，0），将A点向右平移3个单位长度，再向上平移3个单位长度，得到点B，直线y=2x+m经过点B，与y轴交于点C．

(1)、求点B，C的坐标；

(2)、记二次函数图象的顶点为M，与x轴的两个交点为A、D，写出以AM为一边，AD为对角线的菱形的面积S关于a的函数解析式；

(3)、若二次函数y=ax²-2ax+c的图象与线段CB恰有一个公共点，结合函数图象，直接写出a的取值范围．

查看试题解析