内蒙古自治区赤峰市松山区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 用配方法解一元二次方程时,方程可变形为( )A、 B、 C、 D、2. 将抛物线向下平移1个单位,再向右平移两个单位后的顶点坐标是( )A、(-4,4) B、(0,4) C、(0,6) D、(-4,-6)3. 观察下列图案,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的点中任取一点C,使△ABC为直角三角形的概率是( )
4. 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的点中任取一点C,使△ABC为直角三角形的概率是( ) A、 B、 C、 D、5. 某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队数是( )A、6 B、7 C、8 D、96. 下列有关圆的一些结论:①直径是圆中最长的弦;②等弧所对的圆心角相等;③平分弦的直径垂直于弦;④对角互补的四边形内接于圆;⑤圆的切线垂直于过切点的半径.其中正确的有( )A、1个 B、2个 C、3个 D、4个7. 如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是( )
A、 B、 C、 D、5. 某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队数是( )A、6 B、7 C、8 D、96. 下列有关圆的一些结论:①直径是圆中最长的弦;②等弧所对的圆心角相等;③平分弦的直径垂直于弦;④对角互补的四边形内接于圆;⑤圆的切线垂直于过切点的半径.其中正确的有( )A、1个 B、2个 C、3个 D、4个7. 如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是( )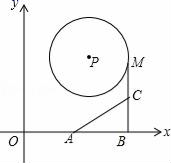 A、1.4 B、 C、 D、2.68. 已知点C是线段AB的黄金分割点,AC>BC,线段AB的长为4,则线段AC的长是( )A、2 -2 B、6-2 C、 -1 D、3-9. 抛物线y=ax²+bx+c(a>0)与直线y=bx+c在同一坐标系中的大致图像可能为( )A、
A、1.4 B、 C、 D、2.68. 已知点C是线段AB的黄金分割点,AC>BC,线段AB的长为4,则线段AC的长是( )A、2 -2 B、6-2 C、 -1 D、3-9. 抛物线y=ax²+bx+c(a>0)与直线y=bx+c在同一坐标系中的大致图像可能为( )A、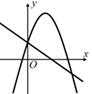 B、
B、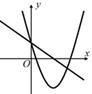 C、
C、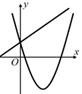 D、
D、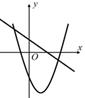 10. 以半径为1的圆内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )A、不能构成三角形 B、这个三角形是等腰三角形 C、这个三角形是直角三角形 D、这个三角形是钝角三角形11. 在下图的四个三角形中,不能由 经过旋转或平移得到的是( )
10. 以半径为1的圆内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )A、不能构成三角形 B、这个三角形是等腰三角形 C、这个三角形是直角三角形 D、这个三角形是钝角三角形11. 在下图的四个三角形中,不能由 经过旋转或平移得到的是( )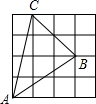 A、
A、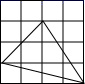 B、
B、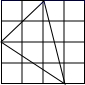 C、
C、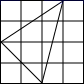 D、
D、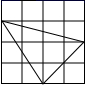 12. 如图,矩形ABCD中, , BC=3,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )
12. 如图,矩形ABCD中, , BC=3,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )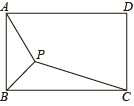 A、 B、 C、 D、13. 如图,把一个量角器与一块30°()角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有点P恰好是量角器的半圆弧中点,连结CP.若BC=4,则CP的长为( )
A、 B、 C、 D、13. 如图,把一个量角器与一块30°()角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有点P恰好是量角器的半圆弧中点,连结CP.若BC=4,则CP的长为( )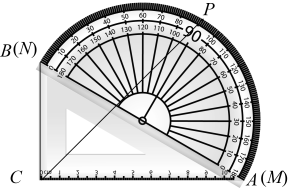 A、 B、 C、 D、14. 从地面竖直向上抛出一小球,小球的高度 (单位: )与小球运动时间 (单位: )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 ;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度 时, .其中正确的是( )
A、 B、 C、 D、14. 从地面竖直向上抛出一小球,小球的高度 (单位: )与小球运动时间 (单位: )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 ;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度 时, .其中正确的是( ) A、①④ B、①② C、②③④ D、②③
A、①④ B、①② C、②③④ D、②③二、填空题
-
15. 1275年,我国南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题:直田积八百六十四步,只云阔不及长一十二步.问阔及长各几步.意思是:矩形面积864平方步,宽比长少12步,问宽和长各几步.若设长为x步,则可列方程为.16. 如图,点A(a,1)、B(-1,b)都在函数(x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是 .
 17. 如图,的半径为2cm,正六边形内接于 , 则图中阴影部分面积为 .
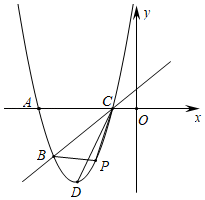
17. 如图,的半径为2cm,正六边形内接于 , 则图中阴影部分面积为 .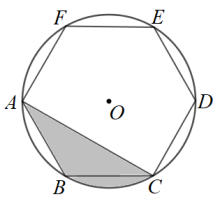 18. 如图,一段抛物线: , 记为 , 它与x轴交于点O,;将绕点旋转180°得 , 交x轴于点;将绕点旋转180°得 , 交x轴于点;…如此进行下去,直至得 , 若在第17段抛物线上,则 .
18. 如图,一段抛物线: , 记为 , 它与x轴交于点O,;将绕点旋转180°得 , 交x轴于点;将绕点旋转180°得 , 交x轴于点;…如此进行下去,直至得 , 若在第17段抛物线上,则 .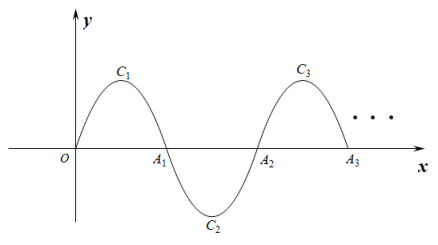
三、解答题
-
19. 关于x的一元二次方程有两个不等实根 .(1)、求实数k的取值范围;(2)、若方程两实根满足 , 求此方程的两个根.20. 已知:的顶点O(0,0),点C在x轴的正半轴上.
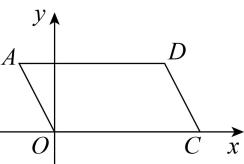 (1)、请你用尺规作出的角平分线,交AD边于点F;(保留痕迹,不写作法)(2)、若点F(2,3),求点A的坐标.21. 2015年7月31日,托马斯巴赫宣布2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市,也是继1952年挪威的奥斯陆举办后时隔70年的第二个举办冬奥会的首都城市,北京冬季奥运会设7个大项,15个分项,109个小项.北京将主办冰上项目,张家口将主办雪上项目,延庆协办张家口举办雪上项目,其中在北京举办的冰上项目共分为A.短道速滑、B.速度滑冰、C.花样滑冰、D.冰球、E冰壶五个小项.体育老师针对某个班级的学生喜欢哪个项目比赛做了调查,并将调查结果制成如下两幅不充整的统计图:
(1)、请你用尺规作出的角平分线,交AD边于点F;(保留痕迹,不写作法)(2)、若点F(2,3),求点A的坐标.21. 2015年7月31日,托马斯巴赫宣布2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市,也是继1952年挪威的奥斯陆举办后时隔70年的第二个举办冬奥会的首都城市,北京冬季奥运会设7个大项,15个分项,109个小项.北京将主办冰上项目,张家口将主办雪上项目,延庆协办张家口举办雪上项目,其中在北京举办的冰上项目共分为A.短道速滑、B.速度滑冰、C.花样滑冰、D.冰球、E冰壶五个小项.体育老师针对某个班级的学生喜欢哪个项目比赛做了调查,并将调查结果制成如下两幅不充整的统计图: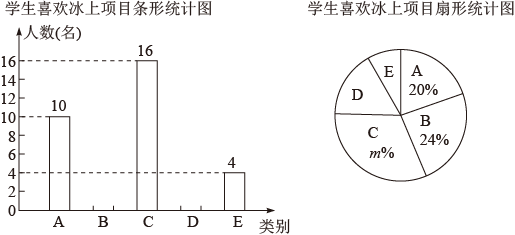
根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生;(2)、请根据以上信息,补全条形统计图;(3)、扇形统计图中的m的值是 , 类别D所对应的扇形圆心角的度数是度.(4)、若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生喜欢速度滑冰?22. 某种病毒传播非常快,如果1人被感染,经过2轮感染后就会有81人被感染.(1)、每轮感染中平均1人会感染几人?(2)、若病毒得不到有效控制,3轮感染后,被感染的人会不会超过700人?23. 如图,中, , AD=AE=3,点B在内,且 , 将AB绕点A逆时针旋转90°得到AC,连接CB,CD,BE.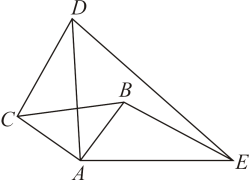 (1)、试探究BE与DC的关系;(2)、当时,连接BD,求出的面积.24. 阅读理解:
(1)、试探究BE与DC的关系;(2)、当时,连接BD,求出的面积.24. 阅读理解:我们学习过二次函数与一元二次方程之间的关系,可以借助二次函数的图象,研究一元二次方程的根.那么我们能否借助二次函数的图象研究一元二次不等式的解集?例如:图一:与x轴的两个交点分别是 , . 此时有两个不相等的实数根 , ;观察图象可以知道:在x轴上方的图象所有点纵坐标大于0,此时对应的x的取值范围是或;所以不等式的解集为:或;类比上述所了解的内容,相信你一定能够解决如下问题:
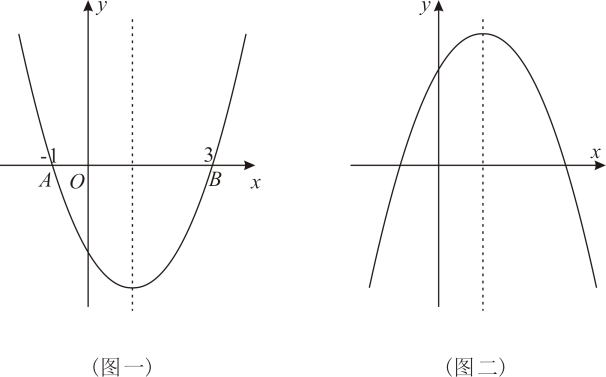 (1)、的解集是: .(2)、图二是把的图象沿x轴翻折而形成的图象,求此二次函数解析式,根据图象求出和的解集.
(1)、的解集是: .(2)、图二是把的图象沿x轴翻折而形成的图象,求此二次函数解析式,根据图象求出和的解集.