内蒙古自治区巴彦淖尔市乌拉特前旗2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1. 从图中的四张印有汽车品牌标志图案的卡片中任取一张，取出印有汽车品牌标志的图案是中心对称图形的卡片的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
2. 如图是由几块小立方块所搭成的几何体的俯视图，小正方体中的数字表示该位置小立方块的个数，则该几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 把抛物线y=12x²﹣1先向右平移1个单位，再向下平移2个单位，得到的抛物线的解析式为（）

A、y=12（x+1）²﹣3 B、y=12（x﹣1）²﹣3 C、y=12（x+1）²+1 D、y=12（x﹣1）²+1

查看试题解析
4. 关于 $x$ 的一元二次方程 $a x^{2} - x + 1 = 0$ 有实数根，则 $a$ 的取值范围是 $($ $)$

A、 $a \leq \frac{1}{4}$ 且 $a \neq 0$ B、 $a \leq \frac{1}{4}$ C、 $a \geq \frac{1}{4}$ 且 $a \neq 0$ D、 $a \geq \frac{1}{4}$

查看试题解析
5.
如图，△ODC是由△OAB绕点O顺时针旋转31°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为100°，则∠DOB的度数是（　　）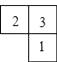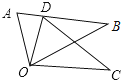

A、34° B、36° C、38° D、40°

查看试题解析
6. 某药品经过两次降价，每瓶零售价由168元降为108元，已知两次降价的百分率相同，设每次降价的百分率为x，根据题意列方程得（）

A、 $168 {(1 - x)}^{2} = 108$ B、 $168 (1 - x^{2}) = 108$ C、 $168 (1 - 2 x) = 108$ D、 $168 {(1 + x)}^{2} = 108$

查看试题解析
7. 如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．∠OAB＝38°，则∠E的度数为（）

A、52° B、38° C、30° D、26°

查看试题解析
8.
如图，已知双曲线y= $\frac{k}{x}$ (k<0)经过直角三角形OAB斜边OA的中点D ，且与直角边AB相交于点C ．若点A的坐标为（-6，4），则△AOC的面积为

A、12 B、9 C、6 D、4

查看试题解析
9. 如图，AB是⊙O的直径，CD是弦，AB⊥CD，垂足为点E，连接OD、CB、AC，∠DOB＝60°，EB＝2，那么CD的长为（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
10.
如图是抛物线y₁=ax²+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y₂=mx+n（m≠0）与抛物线交于A，B两点，下列结论：
①2a+b=0；②abc＞0；③方程ax²+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y₂＜y₁ ，
其中正确的是（　　）

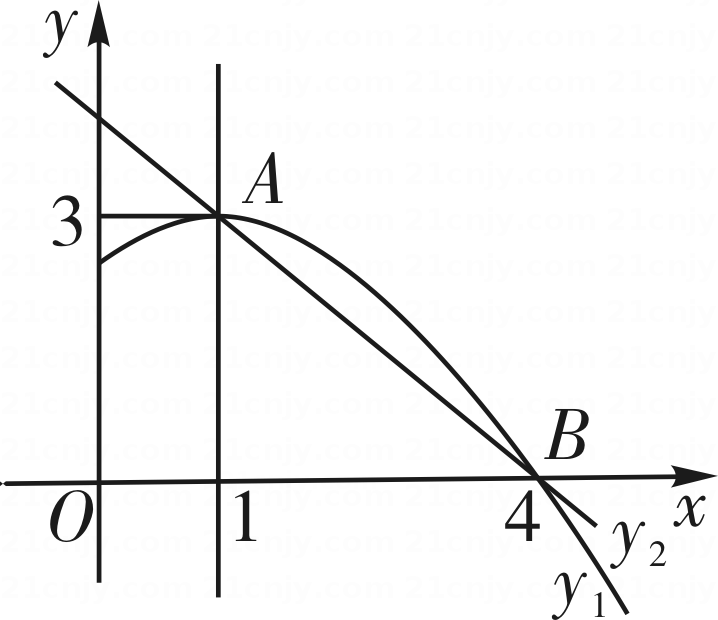A、①②③ B、①③④ C、①③⑤ D、②④⑤

查看试题解析

二、填空题

11. 关于x的一元二次方程x²-mx+2m＝0的一个根为1，则方程的另一根为．

查看试题解析
12. 点P关于原点对称的点Q的坐标是（-1，3），则P的坐标是

查看试题解析
13. 已知二次函数 $y = 3 {(x - 1)}^{2} + k$ 的图象上有三点 $A (\sqrt{2}, y_{1})$ ， $B (2, y_{2})$ ， $C (- \sqrt{5}, y_{3})$ ，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系为．

查看试题解析
14. 如图，AB是⊙O的直径，BD、CD分别是过⊙O上点B、C的切线，且∠BDC=110°.连接AC，则∠A=°.

查看试题解析
15. 扇形半径为3cm，弧长为πcm，则扇形圆心角的度数为．

查看试题解析
16. 如图，在△ABC中，∠BAC＝90°，AB＝AC＝4．将△ABC绕点B逆时针旋转45°，得△A′BC′，则阴影部分的面积为．

查看试题解析
17. 如图，P是正方形ABCD内一点，将△ABP绕点B顺时针旋转90°得到△CBP′，若PB=3，则PP′的长是．

查看试题解析
18. 如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是 $\overset{⌢}{A D}$ 的中点，CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE，CB于点P，Q，连接AC，关于下列结论：①∠BAD＝∠ABC；②GP＝GD；③点P是△ACQ的外心，其中结论正确的是(只需填写序号)．

查看试题解析

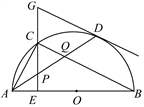
三、解答题

19. 解方程：

(1)、3x²＋2x-5＝0；

(2)、x²-1＝3x-3

查看试题解析
20. 某同学报名参加学校秋季运动会，有以下5个项目可供选择：径赛项目：100m、200m、1000m（分别用A₁、A₂、A₃表示）；田赛项目：跳远，跳高（分别用T₁、T₂表示）．

(1)、该同学从5个项目中任选一个，恰好是田赛项目的概率P为；

(2)、该同学从5个项目中任选两个，求恰好是一个径赛项目和一个田赛项目的概率P₁ ，利用列表法或树状图加以说明；

(3)、该同学从5个项目中任选两个，则两个项目都是径赛项目的概率P₂为．

查看试题解析
21. 为了落实国务院的指示精神，某地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y＝﹣2x＋80，设这种产品每天的销售利润为w元．

(1)、求w与x之间的函数关系式．

(2)、该产品销售价定为每千克多少元时，每天的销售利润最大？最大利润是多少元？

查看试题解析
22. 如图，在平面直角坐标系中，一次函数y＝kx＋b的图象分别交x轴、y轴于A、B两点，与反比例函数y＝ $\frac{m}{x}$ 的图象交于C、D两点，DE⊥x轴于点E，已知C点的坐标是（6，-1），DE＝3

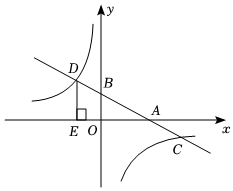(1)、求反比例函数与一次函数的解析式．

(2)、求△DOC的面积．

(3)、根据图象直接回答：当x为何值时，一次函数的值大于反比例函数的值？

查看试题解析
23. 如图，已知⊙O的半径为1，DE是⊙O的直径，过点D作⊙O的切线AD，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形．

(1)、求AD的长；

(2)、BC是⊙O的切线吗？若是，给出证明；若不是，说明理由．

查看试题解析
24. 如图，已知抛物线y＝ax²＋2x＋c与x轴交于点A（-1，0），B，与y轴交于点C（0，3）．

(1)、求抛物线的解析式，并求出点B的坐标；

(2)、点M是线段BC上的点（不与B，C重合），过M作NM∥y轴交抛物线于N，若点M的横坐标为m，请用含m的代数式表示MN的长；

(3)、在（2）的条件下，连接NB，NC，是否存在点M，使△BNC的面积最大？若存在，求点M的坐标；若不存在，说明理由．

查看试题解析