内蒙古自治区巴彦淖尔市杭锦后旗2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 下列两个图形:①两个等腰三角形;②两个直角三角形;③两个正方形;④两个矩形;⑤两个菱形;⑥两个正五边形.其中一定相似的有( )A、2组 B、3组 C、4组 D、5组2. 柜子里有两双不同的鞋,如果从中随机地取出2只,那么取出的鞋是同一双的概率为( )A、 B、 C、 D、3. 在下列四个函数中,当 时,y随x的增大而减小的函数是( )A、 B、 C、 D、4. 如图, , 是 的切线, , 为切点, 是 的直径, ,则 的度数为( )
 A、52° B、51° C、61° D、64.5°5. 把点 绕原点顺时针旋转270°,点 的对应点的坐标是( )A、 B、 C、 D、6. 小明设计了一个魔术盒,当任意实数对(a,b),进入其中时,会得到一个新的实数+2b-3.例如把(2,-5)放入其中,就会得到+2×(-5)-3=-9.现将实数对(m,-3m),放入其中,得到实数4,则m的值为( )A、7 B、-1 C、3 D、7或-17. 若函数 的图象如图所示,则函数 和 在同一平面直角坐标系中的图象大致是( )
A、52° B、51° C、61° D、64.5°5. 把点 绕原点顺时针旋转270°,点 的对应点的坐标是( )A、 B、 C、 D、6. 小明设计了一个魔术盒,当任意实数对(a,b),进入其中时,会得到一个新的实数+2b-3.例如把(2,-5)放入其中,就会得到+2×(-5)-3=-9.现将实数对(m,-3m),放入其中,得到实数4,则m的值为( )A、7 B、-1 C、3 D、7或-17. 若函数 的图象如图所示,则函数 和 在同一平面直角坐标系中的图象大致是( )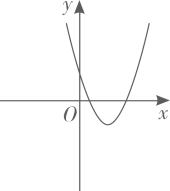 A、
A、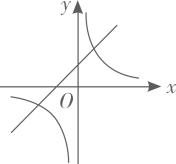 B、
B、 C、
C、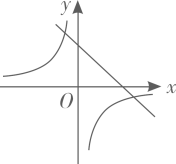 D、
D、 8. 如图所示,给出下列条件:① ;② ;③ ;④ ,其中单独能够判定 的个数为( )
8. 如图所示,给出下列条件:① ;② ;③ ;④ ,其中单独能够判定 的个数为( ) A、 B、 C、 D、9. 如图,在 中, , , ,以点A为圆心,AC的长为半径画弧,交AB于点D , 交AC于点C , 以点B为圆心,AC的长为半径画弧,交AB于点E , 交BC于点F , 则图中阴影部分的面积为( )
A、 B、 C、 D、9. 如图,在 中, , , ,以点A为圆心,AC的长为半径画弧,交AB于点D , 交AC于点C , 以点B为圆心,AC的长为半径画弧,交AB于点E , 交BC于点F , 则图中阴影部分的面积为( ) A、 B、 C、 D、10. 下列结论中:① 的内切圆半径为 , 的周长为 ,则 的面积是 ;②同时抛掷两枚质地均匀的硬币,两枚硬币全部正面向上的概率为 ;③圆内接平行四边形是矩形;④无论 取何值,方程 总有两个不等的实数根.其中正确的结论有( )A、4个 B、3个 C、2个 D、1个
A、 B、 C、 D、10. 下列结论中:① 的内切圆半径为 , 的周长为 ,则 的面积是 ;②同时抛掷两枚质地均匀的硬币,两枚硬币全部正面向上的概率为 ;③圆内接平行四边形是矩形;④无论 取何值,方程 总有两个不等的实数根.其中正确的结论有( )A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 正比例函数 与反比例函数 的图象交于A , B两点,若A点坐标为 ,则 .12. 已知圆锥的母线长为10,高为8,则该圆锥的侧面展开图(扇形)的弧长为 . (用含π的代数式表示),圆心角为度.13. 动物学家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,据此若设刚出生的这种动物共有a只.则20年后存活的有只,现年20岁的这种动物活到25岁的概率是 .14. 如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,若线段AE=5,则S四边形ABCD= .
 15. 下列四个二次函数:① ,② ,③ ,④ .其中抛物线开口从大到小的排列顺序是(填序号即可).16. 如图,是圆O的弦, , 垂足为点C,将劣弧沿弦折叠交于的中点D,若 , 则圆O的半径为 .
15. 下列四个二次函数:① ,② ,③ ,④ .其中抛物线开口从大到小的排列顺序是(填序号即可).16. 如图,是圆O的弦, , 垂足为点C,将劣弧沿弦折叠交于的中点D,若 , 则圆O的半径为 .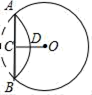 17. 你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢!以方程 即 为例加以说明.数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是 ,其中它又等于四个矩形的面积加上中间小正方形的面积,即 ,据此易得 .那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程 的正确构图是.(只填序号)
17. 你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢!以方程 即 为例加以说明.数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是 ,其中它又等于四个矩形的面积加上中间小正方形的面积,即 ,据此易得 .那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程 的正确构图是.(只填序号)
三、解答题
-
18. 按要求解下列方程(1)、 (配方法)(2)、 (因式分解法)19. 防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.(1)、小明从A测温通道通过的概率是;(2)、利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.20. 某超市经销一种商品,每千克成本为40元,每周可卖出300千克,经试销发现,该种商品每千克涨价1元,每周就少卖10千克,该商品的现销售单价60(元/千克),若该种商品每千克涨价x元(0<x<10).(1)、根据题意填写下表:
销售单价x(元/千克)
每千克利润(元)
每周销售量(千克)
每周利润(元)
现在
60
300
涨价后
20+x
(2)、为保证每周获得6090元的销售利润,则商品每千克应涨价多少元?21. 在△ABC中.BC边的长为x,BC边上的高为y,△ABC的面积为2. (1)、y关于x的函数关系式是 , x的取值范围是;(2)、在平面直角坐标系中画出该函数图象;(3)、将直线y=-x+3向上平移a(a>0)个单位长度后与上述函数图象有且只有一个交点,请求出此时a的值.22. 如图,已知三角形ABC的边AB是圆O的切线,切点为B. AC经过圆心O并与圆相交于点D,C,过C作直线CE丄AB,交AB的延长线于点E,
(1)、y关于x的函数关系式是 , x的取值范围是;(2)、在平面直角坐标系中画出该函数图象;(3)、将直线y=-x+3向上平移a(a>0)个单位长度后与上述函数图象有且只有一个交点,请求出此时a的值.22. 如图,已知三角形ABC的边AB是圆O的切线,切点为B. AC经过圆心O并与圆相交于点D,C,过C作直线CE丄AB,交AB的延长线于点E,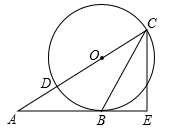 (1)、求证:CB平分∠ACE;(2)、若BE=3,CE=4,求圆O的半径.23. 综合与实践
(1)、求证:CB平分∠ACE;(2)、若BE=3,CE=4,求圆O的半径.23. 综合与实践问题情境:

如图①,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△(点A的对应点为点C).延长AE交于点F,连接DE.
猜想证明:
(1)、试判断四边形的形状,并说明理由;(2)、如图②,若DA=DE,请猜想线段CF与的数量关系并加以证明;(3)、解决问题:如图①,若AB=5,CF=1,请直接写出DE的长.
24. 如图,抛物线 与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l: 与y轴交于点C,与抛物线 的另一个交点为D,已知 ,P点为抛物线 上一动点(不与A、D重合). (1)、求抛物线和直线l的解析式;(2)、当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作 轴交直线l于点F,求 的最大值;(3)、设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(1)、求抛物线和直线l的解析式;(2)、当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作 轴交直线l于点F,求 的最大值;(3)、设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.