内蒙古霍林郭勒市2021-2022学年九年级上学期期末考试数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 抛物线y＝（x−2）²＋3的顶点坐标是（）

A、（2，3） B、（－2，3） C、（2，－3） D、（－2，－3）

查看试题解析
3. 随机从下列命题中选择一个命题，是真命题的概率是（）
①3是9的平方根；②在同圆或等圆中，相等的弦所对的圆周角相等；③三点确定一个圆；④三角形三条中线的交点到三个顶点的距离相等．

A、1 B、 $\frac{3}{4}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
4. 已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是（）

A、30° B、60° C、30°或150° D、60°或120°

查看试题解析
5. 若菱形ABCD的一条对角线长为8，边CD的长是方程x²﹣10x+24＝0的一个根，则该菱形ABCD的周长为（）

A、16 B、24 C、16或24 D、48

查看试题解析
6. 将二次函数y=x²的图象先向下平移1个单位，再向右平移3个单位，得到的图象与一次函数y=2x+b的图象有公共点，则实数b的取值范围是（）

A、b＞8 B、b＞﹣8 C、b≥8 D、b≥﹣8

查看试题解析
7. 如图，若干全等正五边形排成形状，图中所示的是前3个正五边形，则要完成这一圆环还需这样的正五边形（）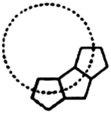

A、6个 B、7个 C、9个 D、10个

查看试题解析
8. 如图，AB⊥OB，AB=2，OB=4，把∠ABO绕点O顺时针旋转60°得∠CDO，则AB扫过的面积（图中阴影部分）为（　　）

A、2 B、2π C、 $\frac{2}{3}$ π D、π

查看试题解析
9. 如图，在矩形ABCD中，AB=1，BC=2，将其折叠，使AB边落在对角线AC上，得到折痕AE，则点E到点B的距离为（）

A、 $\frac{\sqrt{2} - 1}{2}$ B、 $\frac{\sqrt{3} - 1}{2}$ C、 $\frac{\sqrt{5} - 1}{2}$ D、 $\frac{\sqrt{6} - 1}{2}$

查看试题解析
10. 如图，正方形ABCD的边长为3cm，点P从点A出发沿AB→BC→CD以3cm/s的速度向终点D匀速运动，同时，点Q从点A出发沿AD以1cm/s的速度向终点D匀速运动，设P点运动的时间为ts，△APQ的面积为Scm² ，下列选项中能表示S与t之间函数关系的是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 钟表分针的运动可看作是一种旋转现象，一只标准时钟的分针匀速旋转，经过15分钟旋转了度．

查看试题解析
12. 已知扇形的圆心角为120°，半径为6，则扇形的弧长是

查看试题解析
13.
如图所示，在同一坐标系中，作出①y=3x²②y= $\frac{1}{2}$ x²③y=x²的图象，则图象从里到外的三条抛物线对应的函数依次是（填序号）

查看试题解析
14. 如图，将三个同样的正方形的一个顶点重合放置，那么∠1的度数为．

查看试题解析
15. 如图，一飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是.

查看试题解析
16. 已知某工厂计划经过两年的时间，把某种产品从现在的年产量100万台提高到121万台，那么每年平均增长率是．按此年平均增长率，预计第4年该工厂的年产量应为万台．

查看试题解析
17. 如图，若将图1正方形剪成四块，恰能拼成图2的矩形，设a=1，则b= ．

查看试题解析

三、解答题

18. 解下列方程：

(1)、 $x^{2} - 8 x + 1 = 0$ （配方法）

(2)、 $3 x (x - 1) = 2 - 2 x$ ．

查看试题解析
19. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（-5，1），B（-2，2），C（-1，4），请按下列要求画图：

（ 1 ）将△ABC先向右平移4个单位长度、再向下平移1个单位长度，得到△A₁B₁C₁ ，画出△A₁B₁C₁；

（ 2 ）画出与△ABC关于原点O成中心对称的△A₂B₂C₂ ，并直接写出点A2的坐标．

查看试题解析
20. 已知：如图，在△ABC中，∠B＝90°，AB＝5cm，BC＝7cm．点P从点A开始沿AB边向点B以1cm／s的速度移动，点Q从点B开始沿BC边向点C以2cm／s的速度移动，当Q到达点C时，点Q、P同时停止移动．

(1)、如果点P，Q分别从点A，B同时出发，那么几秒后，△PBQ的面积为4cm²？

(2)、如果点P，Q分别从点A，B同时出发，那么几秒后，PQ的长度为5cm？

查看试题解析
21. 在一个不透明的盒子里有5个小球，分别标有数字-3，-2，-1，- $\frac{1}{2}$ ， - $\frac{1}{3}$ ，这些小球除所标的数不同外其余都相同，先从盒子随机摸出1个球，记下所标的数，再从剩下的球中随机摸出1个球，记下所标的数．

(1)、用画树状图或列表的方法求两次摸出的球所标的数之积不大于1的概率．

(2)、若以第一次摸出球上的数字为横坐标，第二次摸出球上的数字为纵坐标确定一点，直接写出该点在双曲线y= $\frac{1}{x}$ 上的概率．

查看试题解析
22. 某地要建造一个圆形喷水池，在水池中央垂直于水面安装一个花形柱子OA，O恰好在水面中心，安装在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，且在过OA的任一平面上，抛物线的形状如图（1）和（2）所示，建立直角坐标系，水流喷出的高度y（米）与水平距离x（米）之间的关系式是y=﹣x²+2x+ $\frac{5}{4}$ ，请回答下列问题．

(1)、柱子OA的高度为多少米？

(2)、喷出的水流距水平面的最大高度是多少？

(3)、若不计其他因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外？

查看试题解析
23.
如图，AB是⊙O的直径，∠BAC=90°，四边形EBOC是平行四边形，EB交⊙O于点D，连接CD并延长交AB的延长线于点F．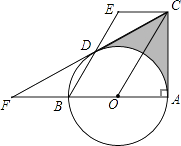

(1)、求证：CF是⊙O的切线；

(2)、若∠F=30°，EB=4，求图中阴影部分的面积（结果保留根号和π）

查看试题解析
24. 阅读理解：
解方程： $x^{3} - x = 0$ ．
解：方程左边分解因式，得
$x (x + 1) (x - 1) = 0$ ，
解得 $x_{1} = 0$ ， $x_{2} = 1$ ， $x_{3} = - 1$ ．
问题解决：

(1)、解方程： $4 x^{3} - 12 x^{2} - x = 0$ ．

(2)、解方程： ${(x^{2} - x)}^{2} - 3 (x^{2} - x) = 0$ ．

(3)、方程 ${(2 x^{2} - x + 1)}^{2} - 2 (2 x^{2} - x) - 5 = 0$ 的解为．

查看试题解析
25. 把一张边长为40 cm的正方形硬纸板，进行适当的裁剪，折成一个长方体盒子(纸板的厚度忽略不计)．

(1)、如图，若在正方形硬纸板的四角各剪掉一个同样大小的正方形，将剩余部分折成一个无盖的长方体盒子．
①要使折成的长方体盒子的底面积为484 cm² ，那么剪掉的正方形的边长为多少？
②折成的长方体盒子的侧面积是否有最大值？如果有，求出这个最大值和此时剪掉的正方形的边长；如果没有，说明理由．

(2)、若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上)，将剩余部分折成一个有盖的长方体盒子．若折成的一个长方体盒子的表面积为550 cm² ，求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况)．

查看试题解析
26. 如图，在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c$ 交 $x$ 轴于点 $A (- 4 ， 0)$ 、 $B (2 ， 0)$ ，交 $y$ 轴于点 $C (0 ， 6)$ ，在 $y$ 轴上有一点 $E (0 ， - 2)$ ，连接 $A E$ .

(1)、求二次函数的表达式；

(2)、若点 $D$ 为抛物线在 $x$ 轴负半轴上方的一个动点，求 $Δ A D E$ 面积的最大值；

(3)、抛物线对称轴上是否存在点 $P$ ，使 $Δ A E P$ 为等腰三角形，若存在，请直接写出所有 $P$ 点的坐标，若不存在请说明理由.

查看试题解析