内蒙古察哈尔右翼前旗2021-2022学年九年级上学期期末考试数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 下列函数不属于二次函数的是( )A、 B、 C、 D、2. 从标号分别为1,2,3,4,5的5张卡片中,随机抽取1张.下列事件中,必然事件是( )
A、标号小于6 B、标号大于6 C、标号是奇数 D、标号是33. 下列标志中,可以看作是中心对称图形的是()A、 B、
B、 C、
C、 D、
D、 4. 一件商品的原价是100元,经过两次提价后的价格为121元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
4. 一件商品的原价是100元,经过两次提价后的价格为121元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
A、100(1+x)=121 B、100(1-x)=121 C、100(1+x)2=121 D、100(1-x)2=1215. 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BOC=40°,则∠D的度数为( )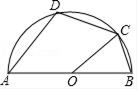 A、100° B、110° C、120° D、130°6. 关于 的一元二次方程 有实数根,则 的取值范围是 ( )A、 B、 C、 D、7. 如图所示,将等腰直角三角形ABC绕点A逆时针旋转15°得到 , 若 , 则图中阴影部分面积为( )
A、100° B、110° C、120° D、130°6. 关于 的一元二次方程 有实数根,则 的取值范围是 ( )A、 B、 C、 D、7. 如图所示,将等腰直角三角形ABC绕点A逆时针旋转15°得到 , 若 , 则图中阴影部分面积为( )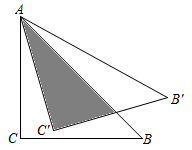 A、 B、 C、 D、8. 从A、B、C三张卡片中任取两张,取到A、B的概率是( )A、 B、 C、 D、9. 函数与在同一直角坐标系中的大致图象可能是( )A、
A、 B、 C、 D、8. 从A、B、C三张卡片中任取两张,取到A、B的概率是( )A、 B、 C、 D、9. 函数与在同一直角坐标系中的大致图象可能是( )A、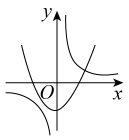 B、
B、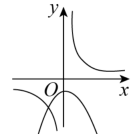 C、
C、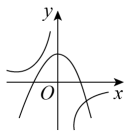 D、
D、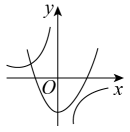 10. 下列图形中,阴影部分面积最大的是( )A、
10. 下列图形中,阴影部分面积最大的是( )A、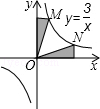 B、
B、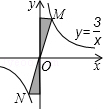 C、
C、 D、
D、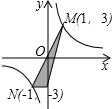
二、填空题
-
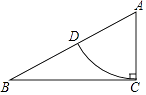
11. 已知直线 y=ax(a≠0)与反比例函数 y= (k≠0)的图象一个交点 坐标为(2,4),则它们另一个交点的坐标是 .12. 如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 . (结果保留π)
 13. 如图,已知在⊙O 中,半径 OA= ,弦 AB=2,∠BAD=18°,OD 与AB 交于点 C,则∠ACO= 度.
13. 如图,已知在⊙O 中,半径 OA= ,弦 AB=2,∠BAD=18°,OD 与AB 交于点 C,则∠ACO= 度.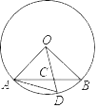 14. 如图,点 A 在双曲线y= 上,点 B 在双曲线y= 上,且AB∥x轴,则△OAB 的面积等于 .
14. 如图,点 A 在双曲线y= 上,点 B 在双曲线y= 上,且AB∥x轴,则△OAB 的面积等于 .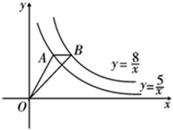 15. 一个三角形的两边长分别为3和6,第三边长是方程x2-10x+21=0的根,则三角形的周长为.16. 若抛物线y=a x 2+bx+c(a≠0)的对称轴为直线x=3,且与x轴的一个交点坐标为(5,0),则一元二次方程a x 2+bx+c =0(a≠0)的根为 .17. 如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是(结果保留π).
15. 一个三角形的两边长分别为3和6,第三边长是方程x2-10x+21=0的根,则三角形的周长为.16. 若抛物线y=a x 2+bx+c(a≠0)的对称轴为直线x=3,且与x轴的一个交点坐标为(5,0),则一元二次方程a x 2+bx+c =0(a≠0)的根为 .17. 如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是(结果保留π). 18. 如图,直线AB,CD,BC分别与相切于点E,G,F,且 , 若 , , 则的长等于 .
18. 如图,直线AB,CD,BC分别与相切于点E,G,F,且 , 若 , , 则的长等于 .
三、解答题
-
19. 关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2 .(1)、求k的取值范围;(2)、如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.20. 如图,已知一次函数y=kx+b的图象与反比例函数y= 的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
 (1)、求一次函数的解析式;(2)、求△AOB的面积.21. 某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区域的可能性相同(若指针指向分界线,则重新转动转盘)
(1)、求一次函数的解析式;(2)、求△AOB的面积.21. 某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区域的可能性相同(若指针指向分界线,则重新转动转盘)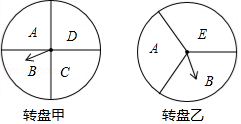 (1)、若顾客选择方式一,则享受9折优惠的概率为多少;(2)、若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.22. 在下面的网格图中,每个小正方形的边长均为1个单位长度,在Rt△ABC中,∠C=90°,AC=3,BC=6.
(1)、若顾客选择方式一,则享受9折优惠的概率为多少;(2)、若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.22. 在下面的网格图中,每个小正方形的边长均为1个单位长度,在Rt△ABC中,∠C=90°,AC=3,BC=6.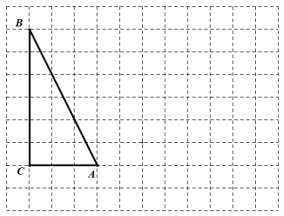 (1)、试作出△ABC以A为旋转中心、沿顺时针方向旋转90°后的△AB1C1;(2)、求点B旋转到B1所经过的路径长;(结果保留π)(3)、若点B的坐标为(-5,5),试建立合适的直角坐标系,并写出A,C两点的坐标;(4)、作出与△ABC关于原点对称的△A2B2C2 , 并写出A2 , B2 , C2三点的坐标.23. 如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)、试作出△ABC以A为旋转中心、沿顺时针方向旋转90°后的△AB1C1;(2)、求点B旋转到B1所经过的路径长;(结果保留π)(3)、若点B的坐标为(-5,5),试建立合适的直角坐标系,并写出A,C两点的坐标;(4)、作出与△ABC关于原点对称的△A2B2C2 , 并写出A2 , B2 , C2三点的坐标.23. 如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.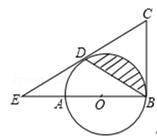 (1)、求证:CD为⊙O的切线;(2)、求证:∠C=2∠DBE.(3)、若EA=AO=2,求图中阴影部分的面积.(结果保留π)24. 甲乙两件服装的进价共500元,商场决定将甲服装按30%的利润定价,乙服装按20%的利润定价,实际出售时,两件服装均按9折出售,商场卖出这两件服装共获利67元.(1)、求甲乙两件服装的进价各是多少元;(2)、由于乙服装畅销,制衣厂经过两次上调价格后,使乙服装每件的进价达到242元,求每件乙服装进价的平均增长率;(3)、若每件乙服装进价按平均增长率再次上调,商场仍按9折出售,定价至少为多少元时,乙服装才可获得利润(定价取整数).25. 如图①,已知抛物线 (a≠0)与 轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
(1)、求证:CD为⊙O的切线;(2)、求证:∠C=2∠DBE.(3)、若EA=AO=2,求图中阴影部分的面积.(结果保留π)24. 甲乙两件服装的进价共500元,商场决定将甲服装按30%的利润定价,乙服装按20%的利润定价,实际出售时,两件服装均按9折出售,商场卖出这两件服装共获利67元.(1)、求甲乙两件服装的进价各是多少元;(2)、由于乙服装畅销,制衣厂经过两次上调价格后,使乙服装每件的进价达到242元,求每件乙服装进价的平均增长率;(3)、若每件乙服装进价按平均增长率再次上调,商场仍按9折出售,定价至少为多少元时,乙服装才可获得利润(定价取整数).25. 如图①,已知抛物线 (a≠0)与 轴交于点A(1,0)和点B(-3,0),与y轴交于点C. (1)、求抛物线的解析式;(2)、设抛物线的对称轴与 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(3)、如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
(1)、求抛物线的解析式;(2)、设抛物线的对称轴与 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(3)、如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.