江西省宜春市高安市2021-2022学年九年级上学期期末数学试题
试卷更新日期：2022-11-07 类型：期末考试
一、单选题
-
1. 将如图所示的图形按逆时针方向旋转90°后得到图形是（ ）
A、
B、
C、
D、
2. 方程的根是（ ）A、 B、 ， C、 ， D、3. 抛物线的顶点坐标是（ ）A、（3，1） B、（3，－1） C、（－3，1） D、（－3，－1）4. 如图，在⊙O中，AB是弦，OC⊥AB，垂足为C，若AB＝16，OC＝6，则⊙O的半径OA等于（ ）
A、16 B、12 C、10 D、85. 如图，点A、C是函数的图像上的任意两点，过点A作x轴的垂线，垂足为B，过点C作y轴的垂线，垂足为D，记的面积为 ， 的面积为 ， 则（ ）.
A、 B、 C、 D、与 大小关系不能确定6. 如图，四边形是扇形的内接矩形，顶点P在弧上，且不与M，N重合，当P点在弧上移动时，矩形的形状、大小随之变化，则的长度（ ）
A、变大 B、变小 C、不变 D、不能确定二、填空题
-
7. 在平面直角坐标系中，点（3，-2）关于原点对称的点的坐标是 ．8. 方程 有两个实数根，则k的取值范围是.9. 将函数的图象向左平移2个单位再向上平移3个单位后的图象所表示的解析式是 ．10. 如图，AB是⊙O的直径，C、D、E都是⊙O上的点，则∠1+∠2＝ ．
11. 如图，中， ， ， ， 则的内切圆半径为 ．
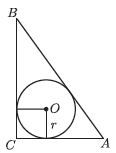12. 如图一次函数y1=kx+b和反比例函数的图象，观察图象写出y1＞y2时，x的取值范围
三、解答题
-
13. 已知抛物线的顶点为且过 ， 求其解析式．14. 在某一电路中，保持电压不变，电流I（安培）与电阻R（欧姆）成反比例，当电阻R=5欧姆时，电流I=2安培．(1)、求I与R之间的函数关系式；(2)、当电流I=0.5安培时，求电阻R的值．15. 如图，在平面直角坐标系中，三角形②、③是由三角形①依次旋转后所得的图形．
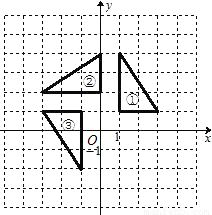
（ 1 ）在图中标出旋转中心P的位置，并写出它的坐标；
（ 2 ）在图上画出再次旋转后的三角形④．
16.作图题：在⊙O 中，点D是劣弧AB的中点，仅用无刻度的直尺画线的方法，按要求完下列作图：
在图（1）中作出∠C的平分线；在图（2）中画一条弦，平分△ABC的面积．
17. 如图，过原点O，且与坐标轴分别交于A、B．点A坐标为 ， M为第三象限弧OB上一点， ， 求的半径．
18. 如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：
(1)、请在图中确定该圆弧所在圆心D点的位置，D点坐标为 ；(2)、连接AD、CD，则⊙D的半径为 ；扇形DAC的圆心角度数为 ；(3)、若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径．19. 经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，如果这三种情况是等可能的， 当三辆汽车经过这个十字路口时：(1)、求三辆车全部同向而行的概率；(2)、求至少有两辆车向左转的概率；(3)、由于十字路口右拐弯处是通往新建经济开发区的，因此交管部门在汽车行驶高峰时段对车流量作了统计，发现汽车在此十字路口向右转的频率为 ，向左转和直行的频率均为 .目前在此路口，汽车左转、右转、直行的绿灯亮的时间分别为30秒，在绿灯亮总时间不变的条件下，为了缓解交通拥挤，请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.20. 如图，PA、PB、CD是的切线，点A、B、E为切点．
(1)、如果的周长为10，求PA的长；(2)、如果 ，①求；
②连AE，BE，求 ．
21.某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度y（微克/毫升）与服药时间x小时之间函数关系如图所示（当4≤x≤10时，y与x成反比例）．
(1)、根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式．(2)、问血液中药物浓度不低于4微克/毫升的持续时间多少小时？22. 如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A、与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．
(1)、试判断BC所在直线与小圆的位置关系，并说明理由；(2)、试判断线段AC、AD、BC之间的数量关系，并说明理由；(3)、若AB=8cm，BC=10cm，求大圆与小圆围成的圆环的面积．（结果保留π）23. 如图，已知直线与x轴、y轴分别交于A、B两点，以为直径作半圆，圆心为C．过A作x轴的垂线AT，M是线段OB上一动点（与O点不重合），过M点作半圆的切线交直线AT于N，交AB于F，切点为P．连接CN、CM．
(1)、证明：；(2)、设 ， ， 求y关于x的函数解析式；(3)、若 ， 当m为何值时，直线AB恰好平分梯形OMNA的面积．