江西省上饶市玉山县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 下面的图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、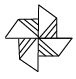 D、
D、 2. 解方程所得结果是( )A、 B、 C、 , D、 ,3. 对于二次函数的图象,下列说法正确的是( )A、开口向下 B、对称轴是 C、顶点坐标是 D、当时,随增大而减小4. 下列事件中属于必然事件的是( )A、正数大于负数 B、下周二,温州的天气是阴天 C、在一个只装有白球的袋子中摸出一个红球 D、在一张纸上任意画两条线段,这两条线段相交5. 如图,已知BD是⊙O的直径,BD⊥AC于点E,∠AOC=100°,则∠OCD的度数是( )
2. 解方程所得结果是( )A、 B、 C、 , D、 ,3. 对于二次函数的图象,下列说法正确的是( )A、开口向下 B、对称轴是 C、顶点坐标是 D、当时,随增大而减小4. 下列事件中属于必然事件的是( )A、正数大于负数 B、下周二,温州的天气是阴天 C、在一个只装有白球的袋子中摸出一个红球 D、在一张纸上任意画两条线段,这两条线段相交5. 如图,已知BD是⊙O的直径,BD⊥AC于点E,∠AOC=100°,则∠OCD的度数是( ) A、20° B、25° C、30° D、40°6. 如图,五边形ABCDE内接于⊙O,若∠CAD=40°,则∠B+∠E的度数是( )
A、20° B、25° C、30° D、40°6. 如图,五边形ABCDE内接于⊙O,若∠CAD=40°,则∠B+∠E的度数是( )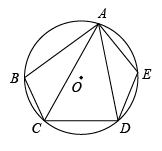 A、200° B、215° C、230° D、220°
A、200° B、215° C、230° D、220°二、填空题
-
7. 把一元二次方程化为一般形式为 .8. 若、是方程的两个根,则 .9. 把抛物线化成一般式是 .10. 一枚质地均匀的骰子,每个面标有的点数是1~6,抛掷骰子,点数是3的倍数的概率是 .11. 如图,△ABC和△DEF关于点O成中心对称,要得到△DEF , 需要将△ABC绕点O旋转角是
 12. 如图,为的切线点A为切点,交于点C,点D在上,连接、、 , 若 , 则的度数为 .
12. 如图,为的切线点A为切点,交于点C,点D在上,连接、、 , 若 , 则的度数为 .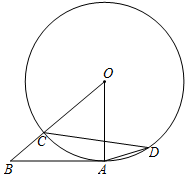 13. 某种植物的主干长出若干数目的支干,每个支干又长出同样多数目的小分支,主干、支干、小分支一共是43个,则每个支干长出的小分支数目为 .14. 如图,已知抛物线与x轴交于A、B两点,与y轴交于点C,顶点为D,其中点B坐标为(3,0),顶点D的横坐标为1,轴,垂足为E,下列结论:①当时,y随x增大而减小;②;③;④;⑤当时, . 其中结论正确的有 . (填序号)(多填错填倒扣一分)
13. 某种植物的主干长出若干数目的支干,每个支干又长出同样多数目的小分支,主干、支干、小分支一共是43个,则每个支干长出的小分支数目为 .14. 如图,已知抛物线与x轴交于A、B两点,与y轴交于点C,顶点为D,其中点B坐标为(3,0),顶点D的横坐标为1,轴,垂足为E,下列结论:①当时,y随x增大而减小;②;③;④;⑤当时, . 其中结论正确的有 . (填序号)(多填错填倒扣一分)
三、解答题
-
15. 解如下方程
(用配方法)
16. 已知关于x 的一元二次方程有两个相等的实数根,求m的值.17. 已知线段为⊙O的弦,且 , 求证: 18. 如图,在中, , D是BC边的中点,交直线AC于点E,请仅用无刻度的直尺,分别按照下列要求作图.
18. 如图,在中, , D是BC边的中点,交直线AC于点E,请仅用无刻度的直尺,分别按照下列要求作图. (1)、在图①中,过点C作AB的垂线;(2)、在图②中,作一条BC的平行线.19. 一个不透明的口袋里有10个除颜色外形状大小都相同的球,其中有4个红球,6个黄球.(1)、若从中随意摸出一个球,求摸出红球的概率;(2)、若从中随意摸出一个球是红球的概率为 , 求袋子中需再加入几个红球?20. 如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE
(1)、在图①中,过点C作AB的垂线;(2)、在图②中,作一条BC的平行线.19. 一个不透明的口袋里有10个除颜色外形状大小都相同的球,其中有4个红球,6个黄球.(1)、若从中随意摸出一个球,求摸出红球的概率;(2)、若从中随意摸出一个球是红球的概率为 , 求袋子中需再加入几个红球?20. 如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE (1)、求证:AD=DE;(2)、求∠DCE的度数.21. 某种病毒传播速度非常快,如果最初有两个人感染这种病毒,经两轮传播后,就有五十个人被感染,求每轮传播中平均一个人会传染给几个人?若病毒得不到有效控制,三轮传播后将有多少人被感染?22. 如图, 中, , ,点 、 分别在边 、 上,且 .
(1)、求证:AD=DE;(2)、求∠DCE的度数.21. 某种病毒传播速度非常快,如果最初有两个人感染这种病毒,经两轮传播后,就有五十个人被感染,求每轮传播中平均一个人会传染给几个人?若病毒得不到有效控制,三轮传播后将有多少人被感染?22. 如图, 中, , ,点 、 分别在边 、 上,且 .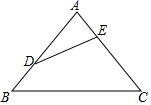 (1)、求 的度数;(2)、将 绕点 逆时针旋转100°,点 的对应点为点 ,连接 ,求证:四边形 为平行四边形.23. 如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,连接AC,OC,BC.
(1)、求 的度数;(2)、将 绕点 逆时针旋转100°,点 的对应点为点 ,连接 ,求证:四边形 为平行四边形.23. 如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,连接AC,OC,BC. (1)、求证:∠1=∠2;(2)、若 , 求⊙O的半径的长.24. 如图(1),抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点B坐标为(2,0),点C坐标为(0,2).
(1)、求证:∠1=∠2;(2)、若 , 求⊙O的半径的长.24. 如图(1),抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点B坐标为(2,0),点C坐标为(0,2). (1)、求抛物线的表达式;(2)、如图(1),点P为直线BC上方抛物线上的一个动点,当△PBC的面积最大时,求点P的坐标;(3)、如图(2),过点M(1,3)作直线MD⊥x轴于点D,在直线MD上是否存在点N,使点N到直线MC的距离等于点N到点A的距离?若存在,求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、如图(1),点P为直线BC上方抛物线上的一个动点,当△PBC的面积最大时,求点P的坐标;(3)、如图(2),过点M(1,3)作直线MD⊥x轴于点D,在直线MD上是否存在点N,使点N到直线MC的距离等于点N到点A的距离?若存在,求出点N的坐标;若不存在,请说明理由.