江西省上饶市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 下列方程属于一元二次方程的是( )A、 B、 C、 D、2. 下面四幅球类的平面图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各式中,y是x的二次函数的是( )A、xy+x2=1 B、x2+y-2=0 C、y2-ax=-2 D、x2-y2+1=04. 下列结论中,正确的是( )A、长度相等的两条弧是等弧 B、相等的圆心角所对的弧相等 C、平分弦的直径垂直于弦 D、圆是中心对称图形5. 下列事件中是必然事件的是( )A、抛掷一枚质地均匀的硬币,正面朝上 B、随意翻到一本书的某页,这一页的页码是偶数 C、打开电视机,正在播放广告 D、从两个班级中任选三名学生,至少有两名学生来自同一个班级6. 在同一直角坐标系中,一次函数y=kx+1与二次函数y=x2+k的大致图象可以是( )A、
3. 下列各式中,y是x的二次函数的是( )A、xy+x2=1 B、x2+y-2=0 C、y2-ax=-2 D、x2-y2+1=04. 下列结论中,正确的是( )A、长度相等的两条弧是等弧 B、相等的圆心角所对的弧相等 C、平分弦的直径垂直于弦 D、圆是中心对称图形5. 下列事件中是必然事件的是( )A、抛掷一枚质地均匀的硬币,正面朝上 B、随意翻到一本书的某页,这一页的页码是偶数 C、打开电视机,正在播放广告 D、从两个班级中任选三名学生,至少有两名学生来自同一个班级6. 在同一直角坐标系中,一次函数y=kx+1与二次函数y=x2+k的大致图象可以是( )A、 B、
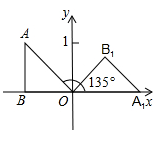
B、 C、
C、 D、
D、
二、填空题
-
7. 函数为开口向下的抛物线,则m= .8. 《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:已知矩形门的高比宽多 尺,门的对角线长 尺,那么门的高和宽各是多少?如果设门的宽为 尺,根据题意,那么可列方程 .9. 某鱼塘里养了条鲤鱼、若干条草鱼和条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为 .10. 平面直角坐标系上的三个点 , 将绕点O按顺时针旋转则点A、B的对应点、的坐标分别是 , .
 11. 设x1 , x2是一元二次方程2x2﹣3x﹣10=0的两根,则 = .12. 如图,在边长为 的正六边形 中,连接 , ,其中点 , 分别为 和 上的动点,若以 , , 为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为 .
11. 设x1 , x2是一元二次方程2x2﹣3x﹣10=0的两根,则 = .12. 如图,在边长为 的正六边形 中,连接 , ,其中点 , 分别为 和 上的动点,若以 , , 为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为 .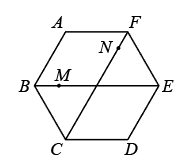
三、解答题
-
13. 用适当的方法解下列方程(1)、 .(2)、 .14. 抛物线的图象与x轴交于A,B两点,利用图象解答下列问题:
 (1)、点A,B的坐标分别是A , B;(2)、若函数值y>0,则x的取值范围是;(3)、函数值y的最小值是;15. 如图,已知AB、CD是⊙O的直径,交⊙O于点F,交⊙O于点E.
(1)、点A,B的坐标分别是A , B;(2)、若函数值y>0,则x的取值范围是;(3)、函数值y的最小值是;15. 如图,已知AB、CD是⊙O的直径,交⊙O于点F,交⊙O于点E. (1)、求证:BE=DF;(2)、写出图中3组不同的且相等的劣弧(不要求证明).16. 请你仅用无刻度的直尺在下面的图中作出△ABC 的边 AB 上的高 CD.
(1)、求证:BE=DF;(2)、写出图中3组不同的且相等的劣弧(不要求证明).16. 请你仅用无刻度的直尺在下面的图中作出△ABC 的边 AB 上的高 CD.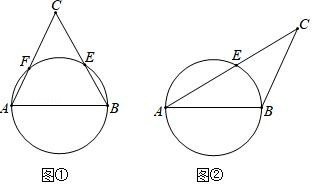 (1)、如图①,以等边三角形 ABC 的边 AB 为直径的圆,与另两边 BC、AC 分别交于点 E、F.(2)、如图②,以钝角三角形 ABC 的一短边 AB 为直径的圆,与最长的边 AC 相交于点 E.17. 一个不透明的口袋里装有分别标有汉字“喜”、“迎”、“峰”、“会”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.(1)、若从中任取一个球,求球上的汉字刚好是“峰”的概率;(2)、从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求取出的两个球上的汉字恰能组成“喜迎”或“峰会”的概率.18. 某水果批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量将减少20千克.(1)、若该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?(2)、商场利润能否达到6200元,若能请求出每千克应涨价多少元;若不能,请说明理由.19. 如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)、如图①,以等边三角形 ABC 的边 AB 为直径的圆,与另两边 BC、AC 分别交于点 E、F.(2)、如图②,以钝角三角形 ABC 的一短边 AB 为直径的圆,与最长的边 AC 相交于点 E.17. 一个不透明的口袋里装有分别标有汉字“喜”、“迎”、“峰”、“会”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.(1)、若从中任取一个球,求球上的汉字刚好是“峰”的概率;(2)、从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求取出的两个球上的汉字恰能组成“喜迎”或“峰会”的概率.18. 某水果批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量将减少20千克.(1)、若该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?(2)、商场利润能否达到6200元,若能请求出每千克应涨价多少元;若不能,请说明理由.19. 如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE. (1)、求证:△AEB ≌△ADC;(2)、连接DE,若∠ADC=105°,求∠BED的度数.20. 如图,在△ABC中,AB=BC,以BC为直径作⊙ O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G.
(1)、求证:△AEB ≌△ADC;(2)、连接DE,若∠ADC=105°,求∠BED的度数.20. 如图,在△ABC中,AB=BC,以BC为直径作⊙ O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G. (1)、求证:EG是⊙O的切线;(2)、若BG=OB,AC=6,求BF的长.21. 为迎接“双十一”购物节,某网店计划销售某种网红食品,进价为20元/千克,经市场调研发现,该食品的售价x(元/千克)的范围为:20≤x≤50,日销售量y(千克)与售价x(元/千克)之间存在一次函数关系,部分图象如图所示:
(1)、求证:EG是⊙O的切线;(2)、若BG=OB,AC=6,求BF的长.21. 为迎接“双十一”购物节,某网店计划销售某种网红食品,进价为20元/千克,经市场调研发现,该食品的售价x(元/千克)的范围为:20≤x≤50,日销售量y(千克)与售价x(元/千克)之间存在一次函数关系,部分图象如图所示: (1)、求y与x之间的函数解析式;(2)、该网店店主热心公益事业,决定从每天的销售利润中捐出200元给灾区,若捐款后店主的剩余利润是800元,求该食品的售价;(3)、若该食品的日销量不低于90千克,当售价为 元/千克时,每天获取的利润最大,最大利润是 元.22.
(1)、求y与x之间的函数解析式;(2)、该网店店主热心公益事业,决定从每天的销售利润中捐出200元给灾区,若捐款后店主的剩余利润是800元,求该食品的售价;(3)、若该食品的日销量不低于90千克,当售价为 元/千克时,每天获取的利润最大,最大利润是 元.22. 如图1,四边形ABCD,将顶点为A的角绕着顶点A顺时针旋转,若角的一条边与DC的延长线交于点F,角的另一条边与CB的延长线交于点E,连接EF.(1)、特例发现 若四边形ABCD为正方形,当∠EAF=45°时,则EF、DF、BE满足数量关系为;(2)、深入探究 如图2,如果在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,当∠EAF=∠BAD时,则EF、DF、BE满足数量关系为;(3)、如图3,如果四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=∠BAD 时,EF与DF、BE之间的数量关系是否发生改变?请给出详细的证明过程;(4)、拓展应用 在(3)中,若BC=4,DC=7,CF=2,求△CEF的周长.23. 如图,已知二次函数L1:y=mx2+2mx﹣3m+1(m≥1)和二次函数L2:y=﹣m(x﹣3)2+4m﹣1(m≥1)图象的顶点分别为M,N,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边).
如图1,四边形ABCD,将顶点为A的角绕着顶点A顺时针旋转,若角的一条边与DC的延长线交于点F,角的另一条边与CB的延长线交于点E,连接EF.(1)、特例发现 若四边形ABCD为正方形,当∠EAF=45°时,则EF、DF、BE满足数量关系为;(2)、深入探究 如图2,如果在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,当∠EAF=∠BAD时,则EF、DF、BE满足数量关系为;(3)、如图3,如果四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=∠BAD 时,EF与DF、BE之间的数量关系是否发生改变?请给出详细的证明过程;(4)、拓展应用 在(3)中,若BC=4,DC=7,CF=2,求△CEF的周长.23. 如图,已知二次函数L1:y=mx2+2mx﹣3m+1(m≥1)和二次函数L2:y=﹣m(x﹣3)2+4m﹣1(m≥1)图象的顶点分别为M,N,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边).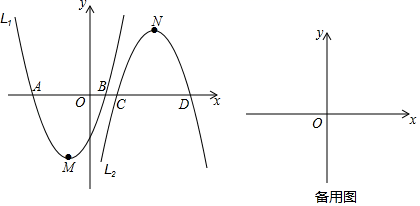 (1)、函数y=mx2+2mx﹣3m+1(m≥1)的顶点坐标为;当二次函数L1 , L2的y值同时随着x的增大而增大时,则x的取值范围是;(2)、当AD=MN时,判断四边形AMDN的形状(直接写出,不必证明);(3)、抛物线L1 , L2均会分别经过某些定点,
(1)、函数y=mx2+2mx﹣3m+1(m≥1)的顶点坐标为;当二次函数L1 , L2的y值同时随着x的增大而增大时,则x的取值范围是;(2)、当AD=MN时,判断四边形AMDN的形状(直接写出,不必证明);(3)、抛物线L1 , L2均会分别经过某些定点,①求所有定点的坐标;
②若抛物线L1位置固定不变,通过左右平移抛物线L2的位置使这些定点组成的图形为菱形,则抛物线L2应平移的距离是多少?