江西省吉安市永丰县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} = 2 x$ 的根是（）

A、 $x = 2$ B、 $x = 0$ C、 $x_{1} = 0, x_{2} = 2$ D、 $x_{1} = 0, x_{2} = - 2$

查看试题解析
2.
如图所示的几何体的左视图是（　　）

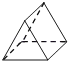A、 B、 C、 D、

查看试题解析
3. 在如图所示的电路中，随机闭合开关S₁、S₂、S₃中的两个，能让灯泡L₁发光的概率是（）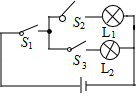

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{4}$

查看试题解析
4. 某反比例函数的图象经过点（-1，6），则此函数图象也经过点 ( ).

A、 $(2, - 3)$ B、 $(- 3, - 3)$ C、 $(2, 3)$ D、 $(- 4, 6)$

查看试题解析
5. 图，在 $△ A B C$ 中，P为AB上一点，在下列四个条件中不能判定 $△ A P C$ 和 $△ A C B$ 相似的条件是（）

A、∠ACP=∠B B、∠APC=∠ACB C、 $A C^{2} = A P \cdot A B$ D、 $A C \cdot C P = A P \cdot C B$

查看试题解析
6. 如图，在Rt△ABC中，∠BAC=90°，D是BC中点，分别以AB，AC为边向外作正方形ABEF和正方形ACGH，连接FD、HD，若BC=10，则阴影部分的面积是（）

A、 $5 \sqrt{2}$ B、 $10 \sqrt{2}$ C、25 D、50

查看试题解析

二、填空题

7. 在一个不透明的盒子中，装有除颜色外完全相同的乒乓球共24个，从中随机摸出一个乒乓球，若摸到黄色乒乓球的概率为 $\frac{3}{8}$ ，该盒子中装有黄色乒乓球的个数是.

查看试题解析
8. 如图，△OAB与△OCD是以点O为位似中心的位似图形，位似比为1：2，∠OCD=90°，CO=CD=2，则点B的坐标为．

查看试题解析
9. 已知a、b是一元二次方程 $x^{2} + 4 x - 1 = 0$ 的两个实数根，求 $a^{2} + a b + 4 a$ 的值．

查看试题解析
10. 等腰三角形ABC中，顶角∠A=36°，BD是∠ABC的角平分线且交AC于点D，则点D是线段AC的黄金分割点，如果 $C D = \sqrt{5} - 1$ ，则AD= ．

查看试题解析
11. 如图是由边长相同的小正方形组成的网格，A，B，P，Q四点均在正方形网格的格点上，线段AB，PQ相交于点M，则图中∠QMB的正切值是

查看试题解析
12. 在矩形ABCD中，AB=4，BC=5，点E在AD边上，若△BCE是等腰三角形，则线段DE的长为．

查看试题解析

三、解答题

13.

(1)、解方程： $x^{2} + 4 x - 3 = 0$ ，

(2)、计算： $- 2^{2} - c o s 60 ° + t a n^{2} 45 °$

查看试题解析
14. 如果 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$ ，且 $3 a - 2 b + c = 8$ ，求 $a - b + c$ 的值．

查看试题解析
15. 在同车道行驶的机动车，后车应当与前车保持一定的安全距离．如图，在一个路口，一辆长为10m的大巴车遇红灯后停在距交通信号灯20m处，小林驾驶一辆小轿车距大车车尾xm，此时红灯、大巴车车顶和小张的眼睛三点刚好在一条直线上，若大巴车车顶高于小林的水平视线0.8m，红灯下沿高于小林的水平视线3.2m，求x的值．

查看试题解析
16. 如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F，若AB=4，BC=6，求DF的长．

查看试题解析
17. 如图，已知正方形ABCD和等边三角形CDE．请你只用无刻度的直尺作图：

(1)、在图1中作∠E的角平分线：

(2)、在图2中作∠ADE的角平分线．

查看试题解析
18. 为了传承优秀传统文化，我校开展“经典诵读”比赛互动，诵读材料有《论语》，《三字经》，《弟子规》（分别用字母 A，B，C依次表示这三个诵读材料），将 A，B，C这三个字母分别写在 3张完全相同的不透明卡片的正面上，把这3张卡片背面朝上洗匀后放在桌面上．小明和小亮参加诵读比赛，比赛时小明先从中随机抽取一张卡片，记录下卡片上的内容，放回后洗匀，再由小亮从中随机抽取一张卡片，选手按各自抽取的卡片上的内容进行诵读比赛．
求：

(1)、小明诵读《论语》的概率．

(2)、小明和小亮诵读两个不同材料的概率．

查看试题解析
19. 某校新建运动场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶．已知看台高为1.6米．为安全起见，要装扶手AB及两根与看台底部FG垂直的架杆AD和BC（杆子的底端分别为D，C），AD=BC=1米，∠DAB约为60°．

(1)、求点D与点C的高度差DH；

(2)、求所用不锈钢材料的总长度．（即AD+AB+BC）．

查看试题解析
20. 新冠病毒肆虐全球，我国的疫情很快得到了控制，并且研发出安全性、有效性均非常高的疫苗，今年七月，国家发布通知，12~17岁未成年人也可接种新冠疫苗.随着全国各地疫苗需求量的急剧增加，经调查发现，北京生物制药厂现有1条生产线最大产能是42万支/天，若每增加1条生产线，每条生产线的最大产能将减少2万支/天，现该厂要保证每天生产疫苗144万支，在既增加产能同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？

查看试题解析
21. 如图，在Rt△ABC中，∠ACB=90°，过点C的直线 $M N ∥ A B$ ， D为AB边上一点，过点D作DE⊥BC，垂足为F，交直线MN于E，连接CD，BE．

(1)、求证：CE=AD：

(2)、当D为AB中点时，证明：四边形BECD是菱形．

(3)、在满足（2）的条件下，当△ABC满足什么条件时，四边形BECD是正方形？说明你的理由．

查看试题解析
22. 如图，在平面直角坐标系中，一次函数 $y_{1} = k x + b (k \neq 0)$ 的图象与反比例函数 $y_{2} = \frac{m}{x} (m \neq 0)$ 的图象交于二、四象限内的A、B两点，与x轴交于C点，点B的坐标为（n，-2），线段OA=5，E为x轴负半轴上一点，且 $s i n ∠ A O E = \frac{4}{5}$ ．

(1)、求该反比例函数和一次函数的解析式：

(2)、求△AOB的面积：

(3)、在反比例函数图象上找一点D，使△ABD的面积等于△AOB的面积，请直接写出点D的坐标．

查看试题解析
23. 定义：我们把两条对角线互相垂直的四边形称为“垂美四边形”．

(1)、特例感知：
如图1，四边形ABCD是“垂美四边形”，如果 $O A = O D = \frac{1}{3} O B$ ， OB=2， $∠ O B C = 60 °$ ，则 $A D^{2} + B C^{2} =$ ， $A B^{2} + C D^{2} =$ ．

(2)、猜想论证
如图1，如果四边形ABCD是“垂美四边形”，猜想它的两组对边AB，CD与BC，AD之间的数量关系并给予证明．

(3)、拓展应用：
如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，∠BAC=60°，求GE长．

(4)、如图3，∠AOB=∠COD=90°，∠ABO=∠CDO=30°，∠BOC=120°，OA=OD， $O C = \sqrt{3}$ ，连接AC，BC，BD，请直接写出BC的长．

查看试题解析