江西省吉安市峡江县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列既是轴对称图形又是中心对称图形的是（）

A、菱形 B、平行四边形 C、等边三角形 D、等腰梯形

查看试题解析
2. 若一元二次方程 $x^{2} - x - 2 = 0$ 的两根为 $x_{1}$ ， $x_{2}$ ，则 $(1 + x_{1}) + x_{2} (1 - x_{1})$ 的值是（）

A、4 B、2 C、1 D、-2

查看试题解析
3. 在如图所示的电路中，随机闭合开关S₁ ， S₂ ， S₃中的两个，能让灯泡L₁发光的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{5}$

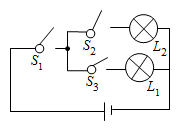查看试题解析
4.
如图，小李打网球时，球恰好打过网，且落在离网4m的位置上，则球拍击球的高度h为（）

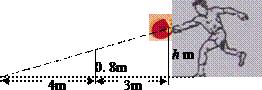A、0.6m B、1.2m C、1.3m D、1.4m

查看试题解析
5. 如图，把抛物线y＝x²沿直线y＝x平移 $\sqrt{2}$ 个单位后，其顶点在直线上的A处，则平移后的抛物线解析式是（）

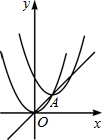A、y＝（x＋1）²－1 B、y＝（x＋1）²＋1 C、y＝（x－1）²＋1 D、y＝（x－1）²－1

查看试题解析
6. 如图，等边三角形 $A B C$ 的边长为4，点O是△ $A B C$ 的中心， $∠ F O G = 12 0^{∘}$ .绕点O旋转 $∠ F O G$ ，分别交线段 $A B 、 B C$ 于 $D 、 E$ 两点，连接 $D E$ ，给出下列四个结论：① $O D = O E$ ；② $S_{Δ O D E} = S_{Δ B D E}$ ；③四边形 $O D B E$ 的面积始终等于 $\frac{4}{3} \sqrt{3}$ ；④△ $B D E$ 周长的最小值为6，上述结论中正确的个数是（）

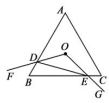A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. 已知α、β均为锐角，且满足 $| s i n α - \frac{1}{2} |$ + $\sqrt{(t a n β - 1)^{2}}$ =0，则α+β= ．

查看试题解析
8. 已知一个正比例函数的图象与一个反比例函数图象的一个交点坐标为(1，3)，则另一个交点坐标是.

查看试题解析
9. 某校九(1)班的学生互赠新年贺卡，共用去1560张贺卡，则九(1)班有名学生．

查看试题解析
10. 如图，菱形ABCD中， $∠ D A B = 60 °$ ， DF⊥AB于点E，且DF=DC，连接FC，则∠ACF的度数为度.

查看试题解析
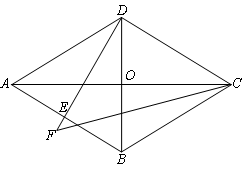11. 如图，是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图，若组成这个几何体的小正方体的块数为n，则n的所有可能值的和为．

查看试题解析
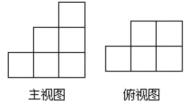12. 如图，矩形ABCD中，AB＝6，AD＝4 $\sqrt{3}$ ，点E是BC的中点，点F在AB上，FB＝2，P是矩形上一动点．若点P从点F出发，沿F→A→D→C的路线运动，当∠FPE＝30°时，FP的长为．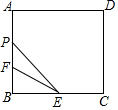

查看试题解析

三、解答题

13. 解方程：

(1)、(2x+1)²=9；

(2)、(x+4)²=3(x+4)．

查看试题解析
14. 如图，在平行四边形ABCD中，AE⊥BC，CF⊥AD，E，F分别为垂足．

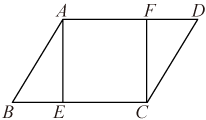(1)、求证：BE=DF；

(2)、求证：四边形AECF是矩形．

查看试题解析
15. 如图，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象与正比例函数y=2x相交于A（1，a），B两点，点C在第四象限，CA∥y轴，AB⊥BC．

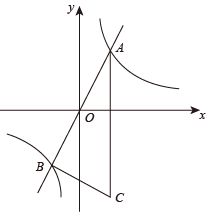(1)、求反比例函数解析式及点B坐标；

(2)、求△ABC的面积．

查看试题解析
16. 如图，在矩形ABCD中，点E为AD的中点，不用圆规、量角器等工具，只用无刻度的直尺作图．

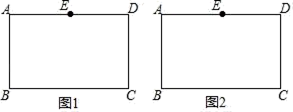(1)、如图1，在BC上找点F，使点F是BC的中点；

(2)、如图2，连接AC，在AC上取两点P，Q，使P，Q是AC的三等分点．

查看试题解析
17. 我国于2019年6月5日首次完成运载火箭海上发射，这标志着我国火箭发射技术达到了一个崭新的高度．如图，运载火箭从海面发射站点 $M$ 处垂直海面发射，当火箭到达点 $A$ 处时，海岸边 $N$ 处的雷达站测得点 $N$ 到点 $A$ 的距离为8千米，仰角为30°．火箭继续直线上升到达点 $B$ 处，此时海岸边 $N$ 处的雷达测得 $B$ 处的仰角增加15°，求此时火箭所在点 $B$ 处与发射站点 $M$ 处的距离．（结果精确到0.1千米）（参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
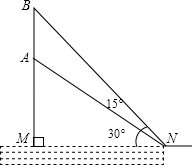18. 如图，在△ABC中，BD平分∠ABC交AC于点D，点E在AB上，且BD²=BE•BC．

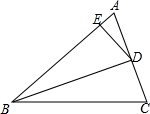(1)、求证：∠BDE=∠C；

(2)、求证：AD²=AE•AB．

查看试题解析
19. 如图，AB∥CD，点E，F分别在AB，CD上，连接EF，∠AEF、∠CFE的平分线交于点G，∠BEF、∠DFE的平分线交于点H．

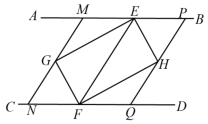(1)、求证：四边形EGFH是矩形；

(2)、小明在完成（1）的证明后继续进行了探索，过G作MN∥EF，分别交AB，CD于点M，N，过H作PQ∥EF，分别交AB，CD于点P，Q，得到四边形MNQP，此时，他猜想四边形MNQP是菱形，他的猜想是否符合题意，请予以说明．

查看试题解析
20. 小聪同学周六到某欢乐谷玩迷宫游戏，从迷宫口A到达迷宫口D有多个路口，如图所示(迷宫的一部分)，规定从迷宫口A到达D处不能重复走同一路线，且小聪走每一条路线的可能性相同．

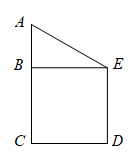(1)、请用画树状图的方法，求小聪同学从迷宫口A到达D处所走的所有可能路线；

(2)、求小聪同学从迷宫口A到达D处经过路口B的概率．

查看试题解析
21. 某商店购进一批成本为每件 30 元的商品，经调查发现，该商品每天的销售量 y（件）与销售单价 x（元）之间满足一次函数关系，其图象如图所示.

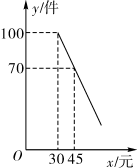(1)、求该商品每天的销售量 y 与销售单价 x 之间的函数关系式；

(2)、若商店按单价不低于成本价，且不高于 50 元销售，则销售单价定为多少，才能使销售该商品每天获得的利润 w（元）最大？最大利润是多少？

(3)、若商店要使销售该商品每天获得的利润不低于 800 元，则每天的销售量最少应为多少件？

查看试题解析
22. 对于两个不相等的有理数a，b，我们规定符号 $m a x {a ， b}$ 表示a，b中的较大值，如 $m a x {2 ， - 3} = 2$ ， $m a x {- 1 ， 0} = 0$ ，请解答下列问题：

(1)、 $m a x {- 1 ， - 1 \frac{2}{5}} =$ ；

(2)、如果 $m a x {x ， 2 - x} = x$ ，求x的取值范围；

(3)、如果 $m a x {x ， 2 - x} = 2 | x - 1 | - 5$ ，求x的值

查看试题解析
23.
如图，抛物线y=ax²+bx（a≠0）经过点A（2，0），点B（3，3），BC⊥x轴于点C，连接OB，等腰直角三角形DEF的斜边EF在x轴上，点E的坐标为（﹣4，0），点F与原点重合

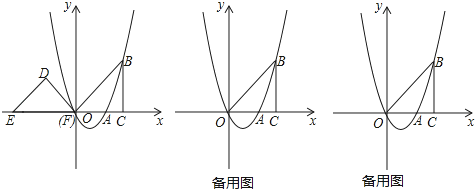(1)、求抛物线的解析式并直接写出它的对称轴；

(2)、△DEF以每秒1个单位长度的速度沿x轴正方向移动，运动时间为t秒，当点D落在BC边上时停止运动，设△DEF与△OBC的重叠部分的面积为S，求出S关于t的函数关系式；

(3)、点P是抛物线对称轴上一点，当△ABP是直角三角形时，请直接写出所有符合条件的点P坐标．

查看试题解析