江西省吉安市泰和县2021-2022学年九年级上学期期末数学试卷
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 二次函数的顶点坐标是( )A、(-2,7) B、(2,7) C、(-2,-7) D、(2,-7)2. 从甲、乙、丙三名男生和A、B两名女生中随机选出一名学生参加问卷调查,则选出女生的可能性是( )A、 B、 C、 D、3. 某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )A、80(1+x)2=100 B、100(1﹣x)2=80 C、80(1+2x)=100 D、80(1+x2)=1004. 关于反比例函数y= , 下列说法中错误的是( )A、它的图象分布在一、三象限 B、当x>-1时,y<-3 C、当x>0时,y的值随x的增大而减小 D、若点(a,b)在它的图象上,则(b,a)也在图象上5. 如图,△ABC中,BD、CE是两条中线,则S△ADE:S△DEF=( )
 A、2:1 B、4:1 C、3:1 D、5:26. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A、2:1 B、4:1 C、3:1 D、5:26. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )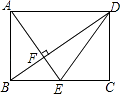 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 若 , 则的值是 .8. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,它的影子QN=1.8m,MN=0.8m,木竿PQ的长度为 .
 9. 如图,在菱形ABCD中,点E是CD上一点,连接AE交对角线BD于点F,连接CF,若∠AED=50°,则∠BCF=度.
9. 如图,在菱形ABCD中,点E是CD上一点,连接AE交对角线BD于点F,连接CF,若∠AED=50°,则∠BCF=度. 10. 一元二次方程x2﹣4x+2=0的两根为x1 , x2 , 则x12﹣4x1+2x1x2的值为 .11. 如图,A、B两点分别在反比例函数(x>0)和(x>0)的图象上,且ABx轴,C为x轴上任意一点,则△ABC的面积为 .
10. 一元二次方程x2﹣4x+2=0的两根为x1 , x2 , 则x12﹣4x1+2x1x2的值为 .11. 如图,A、B两点分别在反比例函数(x>0)和(x>0)的图象上,且ABx轴,C为x轴上任意一点,则△ABC的面积为 .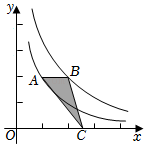 12. 如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是 .
12. 如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是 .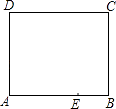
三、解答题
-
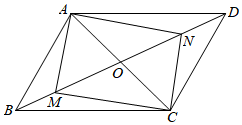
13.(1)、解方程:2(x-1)=x(x-1);(2)、计算:|-3|+4sin45°-tan60°.14. 如图,已知平行四边形ABCD,若M,N是BD上两点,且BM=DN,AC=2MO.
求证:四边形AMCN是矩形.
 15. 已知关于x的一元二次方程x2-(m-3)x-m=0(1)、求证:方程有两个不相等的实数根;(2)、如果方程的两实根为x1、x2 , 且x12+x22-x1x2=7,求m的值。16. 如图,在所给的8×8方格纸中,每个小正方形的边长均相等,小正方形的顶点叫格点,点A,B均在格点上.请画出符合要求的格点四边形(格点四边形是指四边形的各顶点均在小正形的顶点上).
15. 已知关于x的一元二次方程x2-(m-3)x-m=0(1)、求证:方程有两个不相等的实数根;(2)、如果方程的两实根为x1、x2 , 且x12+x22-x1x2=7,求m的值。16. 如图,在所给的8×8方格纸中,每个小正方形的边长均相等,小正方形的顶点叫格点,点A,B均在格点上.请画出符合要求的格点四边形(格点四边形是指四边形的各顶点均在小正形的顶点上).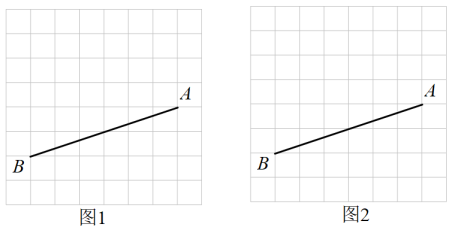 (1)、在图1中画出一个以AB为边的矩形.(2)、在图2中画出一个以AB为对角线的正方形.17. 如图,在△ABC中,∠A=30°,∠B=45°,AC= , 求AB的长.
(1)、在图1中画出一个以AB为边的矩形.(2)、在图2中画出一个以AB为对角线的正方形.17. 如图,在△ABC中,∠A=30°,∠B=45°,AC= , 求AB的长.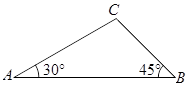
18. 由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达 处时,测得小岛 位于它的北偏东 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛 位于它的北偏东 方向.如果航母继续航行至小岛 的正南方向的 处,求还需航行的距离 的长.(参考数据: , , , , , )
 19. 如图,在矩形ABCD中,对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M,N,与边AD交于点E,垂足为点O.
19. 如图,在矩形ABCD中,对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M,N,与边AD交于点E,垂足为点O. (1)、求证:△AOM≌△CON;(2)、若AB=4,AD=8,求AE的长.20. 为助力泰和县“四城同创”(全国文明城市、全国卫生县城、国家森林城市、省级生态园林城市)工作深入开展,某校组织志愿者进行宣传活动.班主任陈老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
(1)、求证:△AOM≌△CON;(2)、若AB=4,AD=8,求AE的长.20. 为助力泰和县“四城同创”(全国文明城市、全国卫生县城、国家森林城市、省级生态园林城市)工作深入开展,某校组织志愿者进行宣传活动.班主任陈老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,陈老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)、该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;(2)、试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠和小艳被同时抽中”的概率.21. 某商场经营某种品牌的玩具,购进的单价是30元,根据市场调查,在一段时间内,销售单价是40元时,销售量是600元,而销售单价每涨1元,就会少售出10件玩具.(1)、设该种品牌玩具的销售单价为x元,请你分别用x的代数式来表示销售量y件和销售该品牌玩具获利利润W元;(2)、在(1)的条件下,若商场获利了10000元销售利润,求该玩具销售单价x应定为多少元?(3)、在(1)的条件下,若玩具厂规定该品牌玩具销售单价不低于45元,且商场要完成不少于480件的销售任务,求商场销售该品牌玩具获利的最大利润是多少元?22. 如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F. (1)、求证:△PFA∽△ABE;(2)、当点P在射线AD上运动时,设PA=x,是否存在实数x,使以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.23. 如图,抛物线的对称轴为直线x=-1,与x轴相交于A、B两点,与y轴相交于C,OA=OC,点A的坐标为(-3,0).
(1)、求证:△PFA∽△ABE;(2)、当点P在射线AD上运动时,设PA=x,是否存在实数x,使以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.23. 如图,抛物线的对称轴为直线x=-1,与x轴相交于A、B两点,与y轴相交于C,OA=OC,点A的坐标为(-3,0). (1)、求抛物线的表达式;(2)、若点P在抛物线上,且 , 求点P的坐标;(3)、设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
(1)、求抛物线的表达式;(2)、若点P在抛物线上,且 , 求点P的坐标;(3)、设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.