江西省吉安市青原区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，一元二次方程共有（）个
① $x^{2} - 2 x - 1 = 0$ ；② $a x^{2} + b x + c = 0$ ；③ $\frac{1}{x^{2}} + 3 x - 5 = 0$ ；④ $- x^{2} = 0$ ；⑤ $(x - 1)^{2} + y^{2} = 2$ ；⑥ $(x - 1) (x - 3) = x^{2}$ ．

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
2. 某路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当小明到达该路口时，遇到绿灯的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{1}{12}$ D、 $\frac{5}{12}$

查看试题解析
3.
如图，l₁∥l₂∥l₃ ，两条直线与这三条平行线分别交于点A、B、C和D、E、F．已知 $\frac{A B}{B C}$ = $\frac{3}{2}$ ，则 $\frac{D E}{D F}$ 的值为（　　）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
4. 已知矩形的长和宽是方程 $x^{2} - 6 x + 8 = 0$ 的两个实数根，则矩形的对角线的长为（）

A、6 B、7 C、20 D、 $2 \sqrt{5}$

查看试题解析
5. 下列四个命题中：
①一组对边平行且相等的四边形是平行四边形
②一组邻边相等的平行四边形是正方形
③对角线相等的四边形是矩形
④对角线互相垂直平分的四边形是菱形．
正确命题的序号是（）

A、①② B、②③ C、③④ D、①④

查看试题解析
6. 如图，在正方形ABCD中，AB=9，点E在CD边上，且DE=2CE，点P是对角线AC上的一个动点，则PE+PD的最小值是（）

A、3 $\sqrt{10}$ B、10 $\sqrt{3}$ C、9 D、9 $\sqrt{2}$

查看试题解析

二、填空题

7. 已知 $\frac{c}{4}$ = $\frac{b}{5}$ = $\frac{a}{6}$ ≠0，则 $\frac{b + c}{a}$ 的值为

查看试题解析
8. 已知一元二次方程x²－4x－3＝0的两根为m，n，则 $m^{2}$ －mn＋ $n^{2}$ =.

查看试题解析
9. 如图，在菱形 $A B C D$ 中，对角线 $A C ， B D$ 相交于点O，点E在线段BO上，连接AE，若 $C D = 2 B E$ ， $∠ D A E 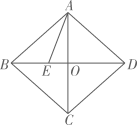= ∠ D E A$ ， $E O = 1$ ，则线段AE的长为．

查看试题解析
10. 有一个人患了新冠肺炎，经过两轮传染后共有169人患了新冠肺炎，每轮传染中平均一个人传染了个人．

查看试题解析
11. 关于 $x$ 的一元二次方程 $(m - 1) x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则 $m$ 的取值范围是．

查看试题解析
12. 已知一个三角形的三边都是方程 $x^{2} - 8 x + 12 = 0$ 的根，则此三角形的周长为．

查看试题解析

三、解答题

13. 计算：

(1)、 $2 s i n 30 ° + 3 c o s 60 ° - 4 t a n 45 °$

(2)、 $2 x^{2} - 5 x - 12 = 0$

查看试题解析
14. 如图，已知菱形ABCD中，对角线AC、BD相交于点O，过点C作CE∥BD，过点D作DE∥AC，CE与DE相交于点E.求证：四边形CODE是矩形；

查看试题解析
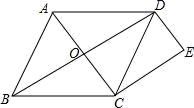15. 如图， $△ A B C$ 是等边三角形，D、E在BC所在的直线上，且 $A B \cdot A C = B D \cdot C E$ ．求证： $△ A B D ∽ △ E C A$ ．

查看试题解析
16. 已知：m、n是方程 $x^{2} - 6 x + 5 = 0$ 的两个实数根，且m＜n，抛物线 $y = - x^{2} + b x + c$ 的图象经过点 $A (- m ， 0)$ ， $B (0 ， n)$ ，求这个抛物线的解析式．

查看试题解析
17. 如图，四边形ABCD中， $∠ B = ∠ C = 50 °$ ， $∠ A = 100 °$ ，请仅用无刻度的直尺，分别按下列要求画图．（保留画图痕迹，不写画法）

(1)、在图（1）中，以AD为腰画一个等腰三角形ADE；

(2)、若 $A B = A D$ ，在图（2）中画一个60°的角．

查看试题解析
18. 一个不透明的布袋里装有2个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率为 $\frac{1}{2}$ 。

(1)、布袋里红球有多少个？

(2)、先从布袋中摸出1个球后不放回，再摸出1个球，请用列表或画树状图等方法求出两次摸到的球都是白球的概率。

查看试题解析
19. 某商场在去年底以每件80元的进价购进一批同型号的服装，一月份以每件150元的售价销售了320件，二、三月份该服装畅销，销量持续走高，在售价不变的情况下，三月底统计知三月份的销量达到了500件

(1)、求二、三月份服装销售量的平均月增长率

(2)、从四月份起商场因换季清仓采用降价促销的方式，经调查发现，在三月份销量的基础上，该服装售价每降价5元，月销售量增加10件，当每件降价多少元时，四月份可获利12000元?

查看试题解析
20. 如图， $∠ A B D = ∠ B C D = 90^{°}$ ，DB平分∠ADC，过点B作 $B M ‖ C D$ 交AD于M．连接CM交DB于N．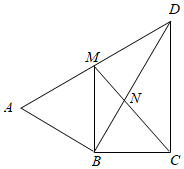

(1)、求证： $B D^{2} = A D \cdot C D$ ；

(2)、若 $C D = 6 ， A D = 8$ ，求MN的长．

查看试题解析
21. 如图，已知一次函数 $y = k x + b$ 的图象与反比例函数 $y = - \frac{8}{x}$ 的图象交于A，B两点，且点A的横坐标和点B的纵坐标都是 $- 2$ ，求：

(1)、一次函数的解析式；

(2)、 $△ A O B$ 的面积．

(3)、根据图象回答：当x为何值时，一次函数的函数值大于反比例函数的函数值．

查看试题解析
22. 阅读下列材料并解答后面的问题：
利用完全平方公式 $(a \pm b)^{2} = a^{2} \pm 2 a b + b^{2}$ ，通过配方可对 $a^{2} + b^{2}$ 进行适当的变形，如： $a^{2} + n^{2} = {(a + b)}^{2} - 2 a b$ 或 $a^{2} + b^{2} = {(a - b)}^{2} + 2 a b ，$ 从而使某些问题得到解决．
例：已知 $a + b = 5 ， a b = 3$ ，求 $a + b$ 的值．
解： $a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 5^{2} - 2 \times 3 = 19 .$
通过对例题的理解解决下列问题：

(1)、已知 $a - b = 2 ， a b = 3$ ，分别求 $a^{2} + b^{2} =$

(2)、若 $a + \frac{1}{a} = 6 ，$ 求 $a^{2} + \frac{1}{a^{2}}$ 的值

(3)、若 $n$ 满足 ${(n - 2019)}^{2} + {(2018 - n)}^{2} = 1$ ，求式子 $(n - 2019) (2018 - n)$ 的值．

查看试题解析
23. 如图，在矩形ABCD中，AB＝8，BC＝16，点P从点D出发向点A运动，运动到点A停止，同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是每秒1个单位，连接PQ、AQ、CP，设点P、Q运动的时间为t秒．

(1)、当t＝时，四边形ABQP是矩形；

(2)、当t＝6时，判断四边形AQCP的形状，并说明理由；

(3)、直接写出以PQ为对角线的正方形面积为96时t的值；

(4)、整个运动当中，线段PQ扫过的面积是．

查看试题解析