江西省吉安市吉州区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 已知5x=6y(y≠0),那么下列比例式中正确的是( )A、 B、 C、 D、
-
2. 用配方法解方程 ,配方后所得的方程是( )A、 B、 C、 D、
-
3. 如图所示的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
4. 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
 A、袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球 B、掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6 C、在“石头、剪刀、布”的游戏中,小宇随机出的是“剪刀” D、掷一枚质地均匀的硬币,落地时结果是“正面向上”
A、袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球 B、掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6 C、在“石头、剪刀、布”的游戏中,小宇随机出的是“剪刀” D、掷一枚质地均匀的硬币,落地时结果是“正面向上” -
5. 如图,函数与的图像相交于点 , 直线与和分别交点B,C,则下列说法中错误的是( )
 A、 B、当时, C、当时, D、当x逐渐增大时,随着x的增大而增大,随着x的增大而减小
A、 B、当时, C、当时, D、当x逐渐增大时,随着x的增大而增大,随着x的增大而减小 -
6. 如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
 A、四边形ACDF是平行四边形 B、当点E为BC中点时,四边形ACDF是矩形 C、当点B与点E重合时,四边形ACDF是菱形 D、四边形ACDF不可能是正方形
A、四边形ACDF是平行四边形 B、当点E为BC中点时,四边形ACDF是矩形 C、当点B与点E重合时,四边形ACDF是菱形 D、四边形ACDF不可能是正方形
二、填空题
-
7. 如图为一个长方体,则该几何体主视图的面积为cm2.
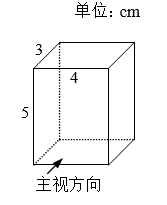
-
8. 若关于 的一元二次方程 的一个解是 ,则 的值是 .
-
9. 如图,在直角坐标系中,△ABC与△ODE是位似图形,其中点 , 则位似中心的坐标是 .

-
10. 一元二次方程的两个实根分别为x1 , x2 , 若x1+x2=1,则x1x2= .
-
11. 《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图, 设门高 为 尺,根据题意,可列方程为.

-
12.
如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= .

三、解答题
-
13. 计算(1)、解方程:(2)、画出图中空心圆柱的主视图、左视图、俯视图.

-
14. 如图,从一个大正方形中截去面积为3cm²和12cm²的两个小正方形,若随机向大正方形内投一粒米,求米粒落在图中阴影部分的概率.

-
15. 已知关于x的一元二次方程有两个不相等的实数根.(1)、求k的取值范围;(2)、若m,n是方程的两根,且 , 求k的值;
-
16. 2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育学习活动,我市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解,今年3月份该基地接待参观人数10万人,5月份接待参观人数增加到12.1万人.(1)、求这两个月参观人数的月平均增长率;(2)、按照这个增长率,预计6月份的参观人数是多少?
-
17. 在正方形ABCD中,E为AB的中点.用无刻度直尺作图,保留作图痕迹;
 (1)、在图1中将△ABD绕点D逆时针旋转90°,(2)、在图2中作以E为顶点的正方形;
(1)、在图1中将△ABD绕点D逆时针旋转90°,(2)、在图2中作以E为顶点的正方形; -
18. 某银行柜台在储户人数较多时常开放1、2、3、4号窗口办理日常业务,一般是先到取号机拿号,按顾客“先到达,先服务”的方式服务,(1)、求某储户在3号窗口办业务的概率是 .(2)、储户乙取号时发现储户甲已办理完业务准备离开(储户甲、乙先后到达银行取号办理业务),请用树状图或列表法求储户甲、乙两人在同一柜台办理业务的概率.
-
19. 如图,在安装路灯AB的路面CD比种植树木的地面PQ高 , 身高的红英MN站在距离C点15米的路面上.在路灯的照射下,路基CP留在地面上的影长EP为0.4米,
 (1)、画出红英MN在地面的影子NF;(2)、若红英留在路面上的影长NF为3m,求路灯AB的高度.
(1)、画出红英MN在地面的影子NF;(2)、若红英留在路面上的影长NF为3m,求路灯AB的高度. -
20. 如图,在平面直角坐标系中,一次函数的图像分别与x轴、y轴交于点A、B,与反比例函数的图像交于点C,连接 . 已知点 , .
 (1)、求b、k的值;(2)、求的面积.
(1)、求b、k的值;(2)、求的面积. -
21. 如图,矩形ABCD中, , 点E、F、G、H,分别是BC、CD、AD、AB上的动点(顶点除外),若;
 (1)、在图1中,点E,F,G,H分别是BC,CD,AD,AB上的中点.
(1)、在图1中,点E,F,G,H分别是BC,CD,AD,AB上的中点.①判断四边形EFGH的形状,并证明;
②若四边形EFGH是正方形,求BC的长;
(2)、在图2中,已知 , 判断四边形EFGH的周长是否会随着点G的变化而变化,如不变化,求出其周长,若会变化,说明理由; -
22. 某数学小组对反比例函数中变量发生变化时进行探究;(1)、问题情景:已知反比例函数中,当自变量x减小3,因变量y减小2后,所得积依然是 , 写出y与x的函数表达式.(2)、活动探究:①列表:根据问题情景中所求函数关系式计算并补全表格.
…
0
1
2
4
5
6
7
8
…
…
2.8
3
4
6
1
1.2
…
②描点:根据表中数据,继续描出①中剩余的点 .
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
 (3)、类比与思考:①结合函数的图象,说出两条不同类型的性质:; .
(3)、类比与思考:①结合函数的图象,说出两条不同类型的性质:; .②所得的函数图象是由的图像如何平移得到 .
(4)、当所得函数值大于1时,x的取值范围是 . -
23. 如图,在四边形ABCD中,G是DC上的点,连接BG,点F是BG上的点,在BC上取点H,使 , 连接HF,CF,AF.
 (1)、①如图1,点F为正方形ABCD中对角线AC上一点,求证:;
(1)、①如图1,点F为正方形ABCD中对角线AC上一点,求证:;②如图2,在正方形ABCD中,若于F,求证: .
(2)、如图3,若四边形ABCD为菱形,①直接写出与之间的数量关系;
②若 , . , , 求AH的长;
