江西省赣州市寻乌县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1.
在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形．该小正方形的序号是（　　）

A、① B、② C、③ D、④

查看试题解析
2. 方程 $(x - 1) (x + 2) = x - 1$ 的解是（）

A、－2 B、1，－2 C、－1，1 D、－1，3

查看试题解析
3. 已知点P关于x轴对称点的坐标是(-1，2)，则点P的坐标为（）

A、(1，2) B、(1，-2) C、(2，-1) D、(-1，-2)

查看试题解析
4. 如图，将△ABC绕点C顺时针旋转90°得到△EDC ．若点A ， D ， E在同一条直线上，∠ACB=20°，则∠ADC的度数是（）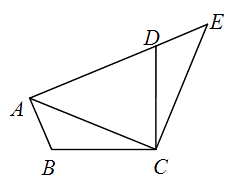

A、55° B、60° C、65° D、70°

查看试题解析
5. 如图，⊙O是△ABC的外接圆，已知∠ABO=50°，则∠ACB的大小为（　　）

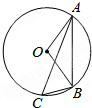A、30° B、40° C、45° D、50°

查看试题解析
6. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴交于点 $(x_{1} ， 0)$ 与 $(x_{2} ， 0)$ ，其中 $x_{1} < x_{2}$ ，方程 $a x^{2} + b x + c - a = 0$ 的两根为m，n（m<n），则下列判断正确的是（）

A、 $m < n < x_{1} < x_{2}$ B、 $b^{2} - 4 a c \leq 0$ C、 $x_{1} + x_{2} > m + n$ D、 $m < x_{1} < x_{2} < n$

查看试题解析

二、填空题

7. “清明时节雨纷纷”是事件．(填“必然”“不可能”或“随机”)

查看试题解析
8. 抛物线 $y = x^{2} - 2 x + 2$ 的对称轴是直线．

查看试题解析
9. 已知圆锥的母线长为10，侧面积为 $30 π$ ，则其侧面展开图的圆心角度数为度．

查看试题解析
10. 已知α、β是一元二次方程x²-2021x+2020=0的两实根，则代数式(α-2021)(β-2021)= ．

查看试题解析
11. 如图，在 $⊙ O$ 中，直径 $A B = 4$ ，弦 $C D ⊥ A B$ 于E，若 $∠ A = 3 0^{∘}$ ，则 $C D =$

查看试题解析
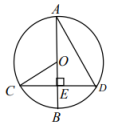12. 如图，已知⊙P的半径是1，圆心P在抛物线 $y = \frac{1}{2} x^{2} - x - \frac{1}{2}$ 上运动，当⊙P与x轴相切时，圆心P的坐标为．

查看试题解析

三、解答题

13.

(1)、解方程： $x^{2} - 4 x - 5 = 0$

(2)、如图，在△ABC中，已知∠ABC＝30°，将△ABC绕点B逆时针旋转50°后得到 $△ A_{1} B C_{1}$ ，若∠A＝100°，求证： $A_{1} C_{1} ∥ B C$ ．

查看试题解析
14. 先化简，再求值： $\frac{m^{2} - 2 m + 1}{m^{2} - 1} \div \frac{m - 2}{m + 1}$ ，其中实数m可使关于x的一元二次方程x²-4x-m＝0有两个相等的实数根．

查看试题解析
15. 如图，AB是⊙O的直径，弦CD⊥AB于点E，连接AC，BC．

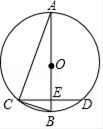(1)、求证：∠A＝∠BCD；

(2)、若AB＝10，CD＝6，求BE的长．

查看试题解析
16. 某同学报名参加校运动会，有以下5个项目可供选择：径赛项目：100m，200m， $400 m ($ 分别用 $A_{1}$ 、 $A_{2}$ 、 $A_{3}$ 表示 $)$ ；田赛项目：跳远，跳高 $($ 分别用 $B_{1}$ 、 $B_{2}$ 表示 $)$ .

(1)、该同学从5个项目中任选一个，恰好是田赛项目的概率为；

(2)、该同学从5个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛项目和一个径赛项目的概率.

查看试题解析
17. 等腰△ABC中， $A B = A C$ ，以AB为直径作圆交BC于点D，请仅用无刻度的直尺．根据下列条件分别在图1、图2中画一条弦，使这条弦的长度等于弦BD．（保留作图痕迹，不写作法，用虚线表示画图过程，实线表示画图结果）

(1)、如图1， $∠ A < 9 0^{∘}$ ；

(2)、如图2， $∠ A > 9 0^{∘}$

查看试题解析
18. 在平面直角坐标系中，△ABC的位置如图所示．（每个小方格都是边长为1个单位长度的正方形）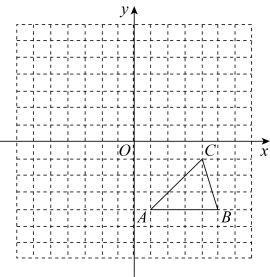
( 1 )画出△ABC关于原点对称的 $△ A^{'} B^{'} C^{'}$ ；
( 2 )将 $△ A^{'} B^{'} C^{'}$ 绕点C′顺时针旋转90°，画出旋转后得到的 $△ A^{″} B^{″} C^{″}$ ，并直接写出此过程中点A′运动的路径长度．（结果保留π）

查看试题解析
19. 如图1，在Rt△ABC中，D为AB的中点，P是BC边上一动点，连接PD，PA．若BC＝4，AC＝3，设PC＝x（当点P与点C重合时，x的值为0）， $P A + P D = y$ ．小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整．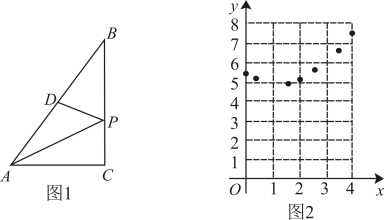

(1)、通过取点、画图、计算，得到了x与y的几组值，如下表：
x
0
0.5
1
1.5
2
2.5
3
3.5
4
y
5.5
5.15
4.94
5.1
5.5
6.7
7.5
说明：补全表格时，相关数值保留一位小数．
（参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{10} \approx 3.162$ ， $\sqrt{13} \approx 3.606$ ）．

(2)、如图2，描出剩余的点，并用光滑的曲线画出该函数的图象．

(3)、观察图象，下列结论正确的有．
①函数有最小值，没有最大值 ②函数有最小值，也有最大值
③当 $x > \frac{4}{3}$ 时，y随着x的增大而增大 ④当y>5.5时，x的取值范围是x>2.5

查看试题解析
20. 某超市对进货价位20元/千克的某种苹果的销售情况进行统计，发现每天销售量y（千克）与销售价x（元/千克）存在一次函数关系，如图所示．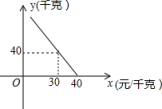

(1)、求y关于x的函数关系式（不要求写出x的取值范围）；

(2)、应怎样确定销售价，使该品种苹果的每天销售利润最大？最大利润是多少？

查看试题解析
21. 如图，在△ABC中，AB＝AC，点D在BC上，BD＝DC，过点D作DE⊥AC，垂足为E，⊙O经过A，B，D三点．

(1)、证明：AB是⊙O的直径

(2)、试判断DE与⊙O的位置关系，并说明理由；

(3)、若DE的长为3，∠BAC＝60°，求⊙O的半径．

查看试题解析
22. 通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．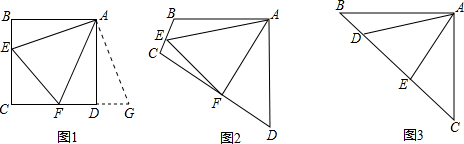
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．

(1)、思路梳理
∵AB=CD，
∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
∵∠ADC=∠B=90°，
∴∠FDG=180°，点F、D、G共线．
根据，易证△AFG≌ ，得EF=BE+DF．

(2)、类比引申
如图2，四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系时，仍有EF=BE+DF．

(3)、联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．

查看试题解析
23. 已知抛物线 $y = a x^{2} + b x + c$ 与x轴只有一个公共点．

(1)、若抛物线过点 $P (0 ， 1)$ ，求a+b的最小值；

(2)、已知点 $P_{1} (- 2 ， 1) ， P_{2} (2 ， - 1) ， P_{3} (2 ， 1)$ 中恰有两点在抛物线上．
①求抛物线的解析式；
②设直线l： $y = k x + 1$ 与抛物线交于M，N两点，点A在直线 $y = - 1$ 上，且 $∠ M A N = 90 °$ ，过点A且与x轴垂直的直线分别交抛物线和直线l于点B，C．求证： $△ M A B$ 与 $△ M B C$ 的面积相等．

查看试题解析

x	0	0.5	1	1.5	2	2.5	3	3.5	4
y	5.5	5.15		4.94	5.1	5.5		6.7	7.5