江西省赣州市信丰县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列品牌汽车的标识是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程2x²-5x＝4的二次项系数、一次项系数、常数项分别为（　　）

A、2，5，4 B、2，-5，4 C、-2，-5，4 D、2，-5，-4

查看试题解析
3. 将抛物线y＝x²向上平移1个单位长度，再向左平移3个单位长度后，得到的抛物线的解析式为（）

A、y＝（x＋3）²＋1 B、y＝（x-3）²＋1 C、y＝（x＋3）²-1 D、y＝（x-3）²-1

查看试题解析
4. 如图，面积为50m²的矩形试验田一面靠墙（墙的长度不限），另外三面用20m长的篱笆围成，平行于墙的边开有一扇1m宽的门（门的材料另计）．设试验田垂直于墙的一边AB为xm，可列方程为（）

A、（20＋1-x）x＝50 B、（20-1-x）x＝50 C、（20＋1-2x）x＝50 D、（20-1-2x）x＝50

查看试题解析
5. 七巧板是古代中国劳动人民的发明，其历史至少可以追溯到公元前一世纪，到了明代基本定型，明、清两代在中国民间广泛流传，清陆以湉《冷庐杂识》卷一中写道：近又有七巧图，其式五，其数七，其变化之式多至千余，体物肖形，随手变幻，盖游戏之具，足以排闷破寂，故世俗皆喜为之，在一次数学活动课上，小明用边长为4cm的正方形纸板制作了如图所示的七巧板，并设计了下列四幅“奔跑者“作品，其中阴影部分的面积为5cm²的是（）

A、 B、 C、 D、

查看试题解析
6. 若二次函数y＝a²x²-bx-c的图象，过不同的六点A（-1，n）、B（5，n-1）C（6，n＋1）、D（ $\sqrt{2}$ ， y₁）、E（2，y₂）、F（4，y₃），则y₁、y₂、y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₂＜y₃＜y₁ D、y₁＜y₃＜y₂

查看试题解析

二、填空题

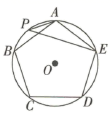
7. 已知 $α ， β$ 是一元二次方程 $x^{2} - 3 x - 2 = 0$ 的两个不相等的实数根，则 $α + β - α β$ 的值为.

查看试题解析
8. 若点A（x₁ ， -6），B（x₂ ， -2），C（x₃ ， 3）在反比例函数y＝- $\frac{1}{x}$ 的图象上，则x₁ ， x₂ ， x₃的大小关系是．（用“＜”表示）

查看试题解析
9. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ， $P$ 为 $\overset{⌢}{A B}$ 上一点，连接 $P A ， P E$ ，则 $∠ A P E$ 的度数为.

查看试题解析
10. 如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为 $α$ （0°＜ $α$ ＜90°），若∠1＝120°，则 $α$ ＝．

查看试题解析
11. 如图，在平面直角坐标系中，⊙D与x轴的正半轴交于A、B两点，与y轴的正半轴相切于点C，连接BC，已知A（2，0），B（6，0），∠ABC＝30°，则阴影部分的面积为．

查看试题解析
12. 如图，已知⊙P的半径为2，圆心P在抛物线y＝ $\frac{1}{2} x^{2}$ +x﹣ $\frac{3}{2}$ 上运动，当⊙P与x轴相切时，则圆心P的坐标为．

查看试题解析

三、解答题

13. 解下列方程：

(1)、x²-6x＋3＝0；

(2)、2x（x-1）＝3-3x．

查看试题解析
14. 学校新冠疫情防控常态化的做法之一，学生进校园必须戴口罩，测体温．某校开通了两种不同类型的测温通道共三条，分别为：红外热成像测温（M通道）和人工测温（N通道和P通道）．在三条通道中，每位同学都要随机选择其中的一条通过．某天早晨，该校小红和小明两位同学将随机通过测温通道进入校园．

(1)、下列事件是必然事件的是：____.（填序号）

A、小红同学从M测温通道通过进入校园 B、小明同学从N测温通道通过进入校园 C、有一位同学从P测温通道通过进入校园 D、两位同学都要从测温通道通过进入校园

(2)、请用列表或画树状图的方法求小红和小明从不同类型测温通道通过进入校园的概率．

查看试题解析
15. 如图，△ABC是⊙O的内接三角形，∠ABC＝45°，请用无刻度的直尺按要求作图.

(1)、如图1，请在图1中画出弦CD，使得CD＝AC．

(2)、如图2，AB是⊙O的直径，AN是⊙O的切线，点B，C，N在同一条直线上请在图中画出△ABN的边AN上的中线BD．

查看试题解析
16. 如图，将线段AB绕点A逆时针旋转 $α$ （0°＜ $α$ ＜60°）得到线段AC，继续旋转2 $α$ 得到线段AD，连接CD、BD

(1)、若 $α$ ＝40°，则∠BDC的度数为°；

(2)、请用含 $α$ 的代数式表示∠BDC，并说明理由．

查看试题解析
17. 已知关于x的方程 $x^{2} + (2 m - 1) x + m^{2} = 0$ 有实数根．

(1)、求m的取值范围；

(2)、设 $α$ ， $β$ 是方程的两个实数根，是否存在实数m使得 $a^{2} + β^{2} - α β = 6$ 成立？如果存在，请求出来；若不存在，请说明理由．

查看试题解析
18. 如图，在平面直角坐标系中，一次函数y₁＝kx＋b图象与x轴交于点A，与）y轴交于点B，与反比例函数y₂＝ $\frac{m}{x}$ 图象交于点C、D，且点C（一2，3），点D的纵坐标是－1．

(1)、求反比例函数与一次函数的解析式；

(2)、若点E是反比例函数在第四象限内图象上的点，过点E作EF⊥y轴，垂足为点F，连接OE、AF，如果S_△BAF＝4S_△EFO ，求点E的坐标．

查看试题解析
19. 如图，O为正方形ABCD对角线上一点，以O为圆心，OA长为半径的⊙O与BC相切于点M ．

(1)、求证：CD与⊙O相切．

(2)、若正方形ABCD的边长为1，求⊙O的半径．

查看试题解析
20. 如图，AB∥CD，AC与BD交于点E，且∠ACB＝90°，AB＝6 $\sqrt{5}$ ，BC＝6，CE＝3．

(1)、求CD的长；

(2)、求证：△CDE∽△BDC．

查看试题解析
21. 我市某电器商场代理销售某种家用空气净化器，其进价是200元/台，经过市场销售后发现，在一个月内，当售价是400元/台时，可售出200台，且售价每降低1元，就可多售出5台，若供货商规定这种空气净化器售价不低于330元/台，代理销售商每月要完成不低于450台的销售任务．

(1)、若某月空气净化器售价降低30元，则该月可售出多少台？

(2)、试确定月销售量 $y$ （台）与售价 $x$ （元/台）之间的函数关系式，并求出售价 $x$ 的范围．

(3)、当售价 $x$ （元/台）定为多少时，商场每月销售这种空气净化器所获的利润 $w$ （元）最大，最大利润是多少？

查看试题解析
22. 在正方形ABCD中，点F在射线AD上（不与A、D重合），连接CF，以CF为对角线作正方形CEFG（C，E，F，G按逆时针排列），连接BE，DG．

(1)、如图1，当点F在线段AD上时，求证：BE＝DG；

(2)、由正方形的性质可知∠CDF＝∠CGF＝90°，即D，G两点均在以CF为直径的同一个圆上．
①请直接回答：∠CDG＝ ▲ °；
②如备用图，当点F在线段AD上时，判断CD、FD、BE三条线段之间的数量关系，并说明理由．
③当点F在线段AD延长线上时，请在备用图2作出图形，直接写出CD、FD、BE三条线段之间的数量关系．

查看试题解析
23. 如图，已知点M（-2，0），a＜0，n为正整数．抛物线C₁：y₁＝a（x-1）²＋k₁交x轴于点M与点A₁（b₁ ， 0），C₂：y₂＝a（x- $\frac{1}{2}$ b₁）²＋k₂交x轴于点M与点A₂（b₂ ， 0），C₃：y₃＝a（x- $\frac{1}{2}$ b₂）²＋k₃交x轴于点M与点A₃（b₃ ， 0），…按此规律，Cn：yn＝a（x- $\frac{1}{2}$ bn_-₁）²＋kn．交x轴于点M与点An（bn，0）．

(1)、填空：b₁＝， b₂＝， b₃＝， An_-₁An＝；

(2)、用含a的代数式表示：抛物线y₃的顶点坐标为；抛物线yn的顶点坐标为；

(3)、设抛物线Cn的顶点为Pn．
①若△MP₁₀A₁₀为等腰直角三角形，求a的值；
②直接写出当a与n满足什么数量关系时，△MPnAn是等腰直角三角形．

查看试题解析