江西省赣州市南康区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1. 以下为四个银行的标志，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件为必然事件的是（）

A、购买二张彩票，一定中奖 B、打开电视，正在播放极限挑战 C、抛掷一枚硬币，正面向上 D、一个盒子中只装有7个红球，从中摸出一个球是红球

查看试题解析
3. 如图，在正方形网格中，△ABC绕某点旋转一定的角度得到 $△ A^{'} B^{'} C^{'}$ ，则旋转中心是点（）

A、O B、P C、Q D、M

查看试题解析
4. 一元二次方程 $x^{2} - 6 x + 4 = 0$ 配方后可化为（）

A、 ${(x - 3)}^{2} = 5$ B、 ${(x - 3)}^{2} = 13$ C、 ${(x + 3)}^{2} = 5$ D、 ${(x + 3)}^{2} = 13$

查看试题解析
5. 斐波那契螺旋线，也称“黄金螺旋线”，自然界中存在许多斐波那契螺旋线的图案（如图1）．图2是根据斐波那契数列1，1，2，3，5，……画出来的螺旋曲线，阴影部分内部是边长为1的正方形，黑色曲线就是斐波那契螺旋线，它是依次在以1，2，3，5为边长的正方形中画一个圆心角为90°的扇形，将其圆弧连接起来得到的．那么这一段斐波那契螺旋线的弧长为（）

A、 $\frac{9}{2} π$ B、 $5 π$ C、 $\frac{11}{2} π$ D、 $6 π$

查看试题解析
6. 已知一个二次函数图象经过 $P_{1} (1 ， y_{1})$ ， $P_{2} (2 ， y_{2})$ ， $P_{3} (3 ， y_{3})$ ， $P_{4} (4 ， y_{4})$ 四点，若 $y_{3} < y_{2} < y_{4}$ ，则 $y_{1} ， y_{2} ， y_{3} ， y_{4}$ 的最值情况是（）

A、 $y_{3}$ 最小， $y_{1}$ 最大 B、 $y_{3}$ 最小， $y_{4}$ 最大 C、 $y_{1}$ 最小， $y_{4}$ 最大 D、无法确定

查看试题解析

二、填空题

7. 从-1， $π$ ， 3中随机任取一数，取到无理数的概率是．

查看试题解析
8. 已知 $x = 1$ 是方程 $x^{2} + b x + 5 = 0$ 的解，则 $b =$ ．

查看试题解析
9. 如图，在△ABC中，∠ACB＝90°，∠B＝36°，以C为圆心，CA为半径的弧交AB于点E，交BC于点D，则∠DCE的度数为°．

查看试题解析
10. 若m，n是方程 $x^{2} + 2 x - 3 = 0$ 两个根，则 $m^{2} n + m n^{2}$ 的值为．

查看试题解析
11. 如图，在菱形ABCD中，AB＝2，∠BAD＝60°，将菱形ABCD绕点A逆时针方向旋转，得到菱形AEFG．当点E恰好落在AC上时，设EF与CD交于点H，则HE＝．

查看试题解析
12. 若二次函数 $y = - x^{2} + m x$ 在－2≤x≤1时的最大值为3，那么m的值是．

查看试题解析

三、解答题

13.

(1)、解方程： $x^{2} - 4 x = 0$ ．

(2)、如图，已知弓形的弦长AB＝8，弓高CD＝2（CD⊥AB并经过圆心O）．求弓形所在⊙O的半径r的长．

查看试题解析
14. 已知点 $P (a ， a + b)$ 与点 $Q (2 b ， 6)$ 关于原点对称，求点P、Q两点的坐标，并直接写出PQ的长．

查看试题解析
15. 如图，△ABC内接于 $⊙ O$ ， AB＝AC，D是 $\overset{⌢}{A B}$ 的中点，请仅用无刻度的直尺按要求画图．

(1)、在图1中，画出△ABC中AB边上的中线CE；

(2)、在图2中，画出△ABC中AC边上的中线BF．

查看试题解析
16. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标，共享出行、共享服务、共享物品、共享知识，制成编号为A、B、C、D的四张卡片（除字母和内容外，其余完全相同）.现将这四张卡片背面朝上，洗匀放好.

(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是；

(2)、小沈从中随机抽取一张卡片（不放回），再从余下的卡片中随机抽取一张，请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.（这四张卡片分别用它们的编号A、B、C、D表示）

查看试题解析
17. 在平面直角坐标系中，二次函数图象的顶点为 $A (1 ， - 4)$ 且经过点 $B (3 ， 0)$ ．

(1)、求该二次函数的解析式．

(2)、求直线 $y = - x - 1$ 与该二次函数图象的交点的坐标．

查看试题解析
18. 如图，在平面直角坐标系内，△ABC的三个顶点坐标分别为 $A (2 ， - 4)$ ， $B (4 ， - 4)$ ， $C (1 ， - 1)$ ．
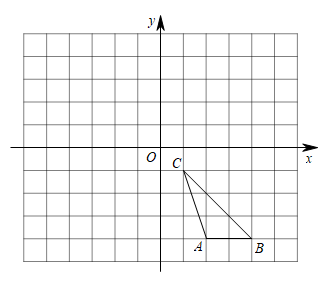
( 1 )画出△ABC关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ，直接写出点 $A_{1}$ 的坐标；
( 2 )画出 $△ A_{1} B_{1} C_{1}$ 绕点O顺时针旋转90°后的 $△ A_{2} B_{2} C_{2}$ ，求出线段 $A_{1} B_{1}$ 扫过的面积（结果保留π）．

查看试题解析
19. 已知二次函数 $y = x^{2} - m x + 2 m - 4$ ．

(1)、求证：无论m取任何实数时，该函数图象与x轴总有交点；

(2)、如果该函数的图象与x轴交点的横坐标均为正数，求m的最小整数值．

查看试题解析
20. 如图，AB是半圆O的直径，D为BC的中点，延长OD交 $\overset{⌢}{B C}$ 于点E，点F为OD的延长线上一点且满足∠B＝∠F．

(1)、求证：CF是⊙O的切线；

(2)、若AB＝4，∠B＝30°，连接AD，求AD的长．

查看试题解析

21. 从下列两题中选择1题完成，两题都完成的仅批改第1题．

(1)、第1题：某宾馆有50个房间供游客居住．当每个房间每天的定价为180元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲．如果游客居住房间，宾馆需对居住的每个房间每天支出20元的各种费用．房价定为多少时，宾馆利润最大?

(2)、第2题：张大爷佩戴能计步的运动手环进行快走锻炼，两次锻炼后整理数据如下表．与第一次锻炼相比，张大爷第二次锻炼时步数在增加，平均步长在减少，其中步数增长的百分率是其平均步长减少的百分率的3倍．设平均步长减少的百分率为x（0<x<0.5）．

	第一次锻炼	第二次锻炼
平均步长（米/步）	0.6	①
步数（步）	10000	②
距离（米）	6000	7020

根据题意完成表格填空

(3)、求平均步长减少的百分率x；【温馨提示：数学运算可以先约分后化简】

(4)、张大爷发现好友中步数排名第一为24000步，因此在两次锻炼结束后又走了500米，使得总步数恰好为24000步，求张大爷这500米的平均步长．

查看试题解析

22. 已知△ABC中，∠ACB＝135°，将△ABC绕点A顺时针旋转90°，得到△AED，连接CD，CE．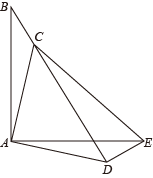

(1)、求证：△ACD为等腰直角三角形；

(2)、若BC＝1，AC＝2，求四边形ACED的面积．

查看试题解析
23. 如图，在△ABC中，∠B＝90°，AB＝12mm，BC＝24mm，动点P从点A开始沿边AB向点B以2mm/s的速度移动，动点Q从点B开始沿边BC向点C以4mm/s的速度移动．如果P，Q两点分别从A，B两点同时出发，请求出△PBQ的面积S与出发时间t的函数解析式及t的取值范围．

查看试题解析
24. 如图，在平面直角坐标系中，矩形ABCD的对称中心为坐标原点O，AD⊥y轴于点E，经过E、D两点的抛物线 $y = - \frac{1}{2} x^{2} + m x + 1 (x \geq 0)$ 的图象记为 $G_{1}$ ，抛物线 $y = - \frac{1}{2} x^{2} - m x - 1 (x < 0)$ 的图象记为 $G_{2}$ ．设矩形ABCD的周长为L．

(1)、当点A的横坐标为－1时，求m的值；

(2)、求L与m之间的函数关系式：

(3)、当 $G_{2}$ 与矩形ABCD恰好有两个公共点时，求L的值.

查看试题解析