江西省赣州市赣县区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列慈善公益图标中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. “网上任意买一张《长津湖》的电影票，票上的排号恰好是奇数”，这个事件是（）

A、必然事件 B、不可能事件 C、确定事件 D、随机事件

查看试题解析
3. 用配方法解一元二次方程 $x^{2} - 9 x + 19 = 0$ ，配方后的方程为（）

A、 ${(x - \frac{9}{2})}^{2} = \frac{5}{4}$ B、 ${(x + \frac{9}{2})}^{2} = \frac{5}{4}$ C、 ${(x - 9)}^{2} = 62$ D、 ${(x + 9)}^{2} = 62$

查看试题解析
4. 如图，AB是⊙O的直径，CD是⊙O的弦，∠CAB＝55°，则∠D的度数是（　　）

A、55° B、45° C、35° D、25°

查看试题解析
5. 如图，在方格纸上建立的平面直角坐标系中，将△ABO绕点O按顺时针方向旋转90°，得△A′B′O，则点A′的坐标为（）

A、（3，1） B、（3，2） C、（2，3） D、（1，3）

查看试题解析
6. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，以下结论中：① $a b c > 0$ ；② $b^{2} - 4 a c > 0$ ；③ $2 a - b = 0$ ；④ $a - b + c > m (a m + b) + c$ （ $m \neq - 1$ 的任意实数）；⑤ $4 a - 2 b + c < 0$ ．正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

7. 已知事件A发生的概率为 $\frac{1}{10}$ ，大量重复做这种试验，事件A平均每100次发生的次数约为次．

查看试题解析
8. 已知x₁、x₂为方程x²-4x＋3＝0的两根，则-x₁-x₂＋2x₁x₂＝．

查看试题解析
9. 如图，在Rt△ABC中，∠C＝90°，AC＝8，BC＝6．若以AC所在直线为轴，把△ABC旋转一周，得到一个圆锥，则这个圆锥的侧面积等于．

查看试题解析
10. 如图，AB为⊙O直径，BC＝4，AC＝3，CD平分∠ACB，则AD＝．

查看试题解析
11. 如图是一个横断面为抛物线形状的拱桥，当水面宽4米时，拱顶(拱桥洞的最高点)离水面2米，水面下降1米时，水面的宽度增加了米．

查看试题解析
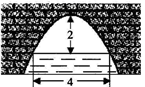12. 如图，在正方形ABCD中，将线段AD绕点A逆时针旋转α°（0＜α＜180）得到线段AE，连接BE、CE．若△EBC是等腰三角形，则α＝．

查看试题解析

三、解答题

13.

(1)、解方程： $x^{2} - 4 x - 5 = 0$ ；

(2)、如图，正方形ABCD内接于⊙O， $\overset{⌢}{A M} = \overset{⌢}{D M}$ ，求证：BM＝CM．

查看试题解析
14. 下表给出了代数式x²＋bx＋c与x的一些对应值：
x
…
0
1
2
3
4
…
x²＋bx＋c
…
3
m
-1
n
3
…

(1)、求出表格中m、n的值；

(2)、设y＝x²＋bx＋c，请直接写出当x取何值时，y＞0

查看试题解析
15. 请用无刻度的直尺，按要求完成下列作图．

(1)、如图1，AB是半圆的直径，△ABC的边AC、BC与半圆分别交于点D、点E，作出△ABC的边AB上的高；

(2)、如图2，AB是半圆的直径，点C、点D是半圆上的两个点，作出四边形ABCD的边AB上的一条垂线．

查看试题解析
16. 赣县区有名的景区很多，其中6处是a．宝莲山风景区，b．寨九坳风景区，c．狮子岩景区，d．白鹭古村景区，e．夏浒旅游景区，f．麂山景区，小明父母计划在春节期间从中选择部分景区游玩．

(1)、小明一家选择去宝莲山风景区游玩的概率是；

(2)、若他们从a，b，c，d四个景区中任选两个景区去游玩，用画树状图或列表的方法求选择a，d两个景区的概率．

查看试题解析
17. 已知关于x的一元二次方程 $x^{2} - 4 x - 2 m + 5 = 0$ 有两个不相等的实数根.

(1)、求实数m的取值范围；

(2)、若该方程的两个根都是符号相同的整数，求整数m的值.

查看试题解析
18. 山水旅行社的一则广告如下：我社组团去A风景区旅游，收费标准为：如果人数不超过30人，人均旅游费用为800元；如果人数多于30人，那么每增加1人，人均旅游费用降低10元，但人均旅游费用不得低于500元，某公司组织一批员工到A风景区旅游，支付给旅行社28000元．

(1)、该公司的人数30人（填“大于、小于或等于”）

(2)、如果设该公司的人数为x，用含x的代数式表示人均旅游费用（填化简结果）

(3)、求（2）中的x．

查看试题解析
19. 如图，已知点P(2m－1，6m－5)在第一象限的角平分线OC 上，AP⊥BP，点A在x轴上，点 B在y轴正半轴上．

(1)、求点P 的坐标；

(2)、当∠APB绕点P旋转时，OA+OB的值是否发生变化？若变化，求出其变化范围；若不变，求出这个定值．

查看试题解析
20. 如图，点C在⊙O上，点P是⊙O直径AB延长线上一点，连接AC，OC，BC，CP，且有BO＝BC＝BP．

(1)、求证：CP是⊙O的切线；

(2)、若OP＝4，求AC的长．

查看试题解析
21. 如图，抛物线y=-x²+bx+c与x轴交于A（2，0），B（-4，0）两点.

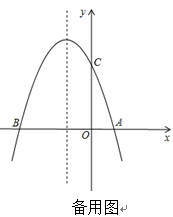(1)、求该抛物线的解析式；

(2)、求出抛物线的对称轴和顶点坐标；

(3)、若抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．

查看试题解析
22. 在△AED中，EA＝ED，∠AED＝α，点F为直线AD上一动点，连接EF，将线段EF绕点E逆时针旋转α，得到线段EG，连接DG．

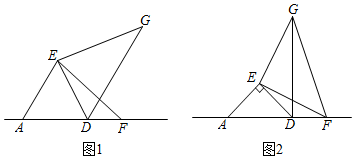(1)、如图1，探究线段AF、DG之间的数量关系；

(2)、如图2，当α＝90°时，其它条件不变，试判断线段DF、AF、GF的数量关系，并证明．

查看试题解析
23. 在平面直角坐标系 $x o y$ 中，规定：抛物线 $y = a {(x - h)}^{2} + k$ 的伴随直线为 $y = a (x - h) + k$ .例如：抛物线 $y = 2 {(x + 1)}^{2} - 3$ 的伴随直线为 $y = 2 (x + 1) - 3$ ，即 $y = 2 x - 1$ ．

(1)、在上面规定下，抛物线 $y = {(x + 1)}^{2} - 4$ 的顶点为．伴随直线为；抛物线 $y = (x + 1)^{2} - 4$ 与其伴随直线的交点坐标为和；

(2)、如图，顶点在第一象限的抛物线 $y = m {(x - 1)}^{2} - 4 m$ 与其伴随直线相交于点 $A ， B$ (点A在点B的右侧)与x轴交于点 $C ， D .$
①若 $∠ C A B = 9 0^{°} ，$ 求m的值；
②如果点 $P (x ， y)$ 是直线 $B C$ 上方抛物线的一个动点， $Δ P B C$ 的面积记为S，当S取得最大值 $\frac{27}{4}$ 时，求m的值．

查看试题解析
24. 【定义】　数学活动课上，谢老师给出如下定义：有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形．

(1)、【理解】如图1，已知A、B、C在格点（小正方形的顶点）上，请用两种不同的方法再画出一个格点D，使四边形ABCD为对等四边形；

(2)、如图2，在圆内接四边形ABCD中，AB是⊙O的直径，AC＝BD．试说明：四边形ABCD是对等四边形；

(3)、如图3，点D，B分别在x轴和y轴上，且B（0，3），∠BDO＝30°，点A是边BD上的一点，且AD：AB＝2，点C在x轴上，且四边形ABOC为对等四边形，请直接写出过点B、C、D的抛物线的解析式．

查看试题解析

x	…	0	1	2	3	4	…
x²＋bx＋c	…	3	m	-1	n	3	…