江西省赣州市定南县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 下列事件中,是必然事件的是( )A、从一个只有白球的盒子里摸出一个球是白球 B、任意买一张电影票,座位号是2的倍数 C、掷一次骰子,向上一面的点数是5 D、画一个三角形,其内角和是360°2. 窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计,窗棂上雕刻有线槽和各种花纹,构成种类繁多的优美图案.下列表示我国古代窗棂样式结构图案中,是中心对称图形但不是轴对称图形的是( )A、
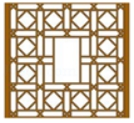 B、
B、 C、
C、 D、
D、 3. 如果关于x的一元二次方程kx2﹣4x-1=0有实数根,那么k应满足的条件是( )A、k>-4 B、 且 C、 且 D、k≤14. 在直角坐标系中,点O为坐标原点,点 , 把线段绕点O顺时针旋转90°得到线段 , 则点的坐标为( ).A、 B、 C、 D、5. 如图, 为 的直径, 为 的弦, 于E,下列说法错误的是( )
3. 如果关于x的一元二次方程kx2﹣4x-1=0有实数根,那么k应满足的条件是( )A、k>-4 B、 且 C、 且 D、k≤14. 在直角坐标系中,点O为坐标原点,点 , 把线段绕点O顺时针旋转90°得到线段 , 则点的坐标为( ).A、 B、 C、 D、5. 如图, 为 的直径, 为 的弦, 于E,下列说法错误的是( )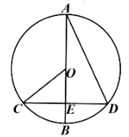 A、 B、 C、 D、6. 已知抛物线y=ax2+bx+3中(a,b是常数)与y轴的交点为A,点A与点B关于抛物线的对称轴对称,二次函数y=ax2+bx+3中(b,c是常数)的自变量x与函数值y的部分对应值如下表:
A、 B、 C、 D、6. 已知抛物线y=ax2+bx+3中(a,b是常数)与y轴的交点为A,点A与点B关于抛物线的对称轴对称,二次函数y=ax2+bx+3中(b,c是常数)的自变量x与函数值y的部分对应值如下表:x
…
-1
0
1
3
4
…
y=ax2+bx+3
…
8
0
0
…
下列结论正确的是( )
A、抛物线的对称轴是x=1 B、当x=2时,y有最大值-1 C、当x<2时,y随x的增大而增大 D、点A的坐标是(0,3)点B的坐标是(4,3)二、填空题
-
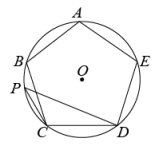
7. 抛物线 的顶点坐标为.8. 在同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为 .9. 如图,正五边形ABCDE内接于⊙O,点P是劣弧上一点(点P不与点C重合),则∠CPD= .
 10. 已知a,b是一元二次方程的两根,则的值是 .11. 如图,铅球运动员掷铅球的高度 (m)与水平距离 (m)之间的函数关系式是: , 则该运动员此次掷铅球的成绩是 m.
10. 已知a,b是一元二次方程的两根,则的值是 .11. 如图,铅球运动员掷铅球的高度 (m)与水平距离 (m)之间的函数关系式是: , 则该运动员此次掷铅球的成绩是 m.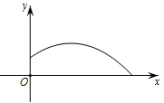 12. 在△ABC中,∠C=90°,∠A=25°,点O是AB的中点,将OB绕点O向三角形外部旋转角时(0°<<180°),得到OP,当△ACP恰为轴对称图形时, 的值为 .
12. 在△ABC中,∠C=90°,∠A=25°,点O是AB的中点,将OB绕点O向三角形外部旋转角时(0°<<180°),得到OP,当△ACP恰为轴对称图形时, 的值为 .三、解答题
-
13.(1)、解方程:x2-5x+6=0;(2)、已知一条抛物线过点(1,3),且顶点坐标为(2,1),求该抛物线解析式.14. 已知关于 的方程 .(1)、若该方程有两个不相等的实数根,求实数 的取值范围:(2)、当该方程的一个根为-3时,求 的值及方程的另一根.15. 在△ABC中,AB=AC,点A在以BC为直径的半圆内,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
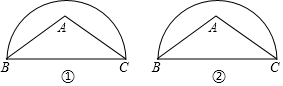 (1)、在图①中作弦EF,使EF∥BC;(2)、在图②中过点A作线段BC的中垂线.16. 小邦和小友两人玩猜数字游戏,先由小友在中心任意想一个数,记为x,然后再由小邦猜小友刚才想的数字,把小邦猜的数字记为y,他们俩想和猜的数字只能在1,2,3,4这四个数字中选取.(1)、“小友想的数字x=3”是事件.(2)、如果小邦猜的数字与小友想的数字相同,则称他们“心灵相通”,求他们心灵相通的概率.17. 如图,在平面直角坐标系中, 的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)、在图①中作弦EF,使EF∥BC;(2)、在图②中过点A作线段BC的中垂线.16. 小邦和小友两人玩猜数字游戏,先由小友在中心任意想一个数,记为x,然后再由小邦猜小友刚才想的数字,把小邦猜的数字记为y,他们俩想和猜的数字只能在1,2,3,4这四个数字中选取.(1)、“小友想的数字x=3”是事件.(2)、如果小邦猜的数字与小友想的数字相同,则称他们“心灵相通”,求他们心灵相通的概率.17. 如图,在平面直角坐标系中, 的三个顶点分别是A(1,3),B(4,4),C(2,1).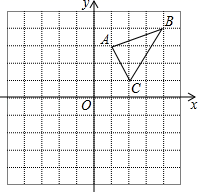
( 1 )把 向左平移4个单位后得到对应的 A1B1C1 , 请画出平移后的 A1B1C1;
( 2 )把 绕原点O旋转180°后得到对应的 A2B2C2 , 请画出旋转后的 A2B2C2;
( 3 )观察图形可知, A1B1C1与 A2B2C2关于点( , )中心对称.
18. 如图,已知AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上,连接OA、DE、BE.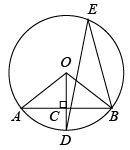 (1)、若∠AOD=60°,求∠DEB的度数;(2)、若CD=2,弦AB=8,求⊙O的半径长.19. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.
(1)、若∠AOD=60°,求∠DEB的度数;(2)、若CD=2,弦AB=8,求⊙O的半径长.19. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.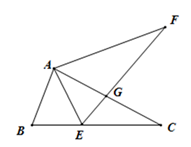 (1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.20. 某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.(1)、从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?(2)、在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?21. 某县古镇地摊上出售一种双肩包,已知这种双肩包的成本价每个20元,市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系: , 设这种双肩包每天的销售利润为w元.(1)、求w与x之间的函数解析式;(2)、这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种双肩包的销售单价不高于48元,该地摊销售这种双肩包每天要获得300元的销售利润,销售单价应定为多少元?22. 如图,AB为半圆的直径,点O为圆心,BC为半圆的切线,连接OC,过半圆上的点D作AD∥OC,连接BD.、的延长线相交于点E.
(1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.20. 某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.(1)、从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?(2)、在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?21. 某县古镇地摊上出售一种双肩包,已知这种双肩包的成本价每个20元,市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系: , 设这种双肩包每天的销售利润为w元.(1)、求w与x之间的函数解析式;(2)、这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种双肩包的销售单价不高于48元,该地摊销售这种双肩包每天要获得300元的销售利润,销售单价应定为多少元?22. 如图,AB为半圆的直径,点O为圆心,BC为半圆的切线,连接OC,过半圆上的点D作AD∥OC,连接BD.、的延长线相交于点E.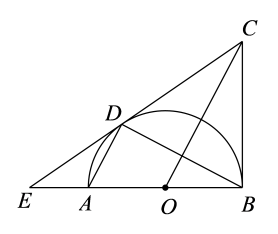 (1)、求证:是的切线;(2)、若 , ,
(1)、求证:是的切线;(2)、若 , ,①求的半径.
②将以点A为中心逆时针旋转 , 求扫过的图形的面积(结果用表示).
23. 在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.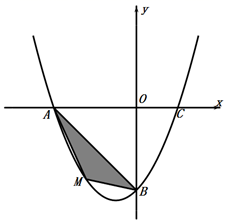 (1)、求抛物线的解析式;(2)、若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.(3)、若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、 O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
(1)、求抛物线的解析式;(2)、若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.(3)、若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、 O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.