江西省赣州市大余县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
1. 在下列四个图案中,不是中心对称图形的是( )A、
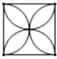 B、
B、 C、
C、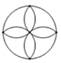 D、
D、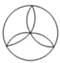 2. 已知正多边形的一个内角是135°,则这个正多边形的边数是( )A、3 B、4 C、6 D、83. 如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=( )
2. 已知正多边形的一个内角是135°,则这个正多边形的边数是( )A、3 B、4 C、6 D、83. 如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=( ) A、125° B、115° C、100° D、130°4. 某公司今年4月的营业额为2500万元,按计划第二季度的总营业额要达到9100万元,设该公司5、6两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( )A、 B、 C、 D、5. 在平面直角坐标系中,把抛物线y=2x2绕原点旋转180°,再向右平移1个单位,向下平移2个单位,所得的抛物线的函数表达式为( )A、y=2(x﹣1)2﹣2 B、y=2(x+1)2﹣2 C、y=﹣2(x﹣1)2﹣2 D、y=﹣2(x+1)2﹣26. 三角形两边长分别是8和6,第三边长是一元二次方程一个实数根,则该三角形的面积是( )A、24 B、48 C、24或 D、
A、125° B、115° C、100° D、130°4. 某公司今年4月的营业额为2500万元,按计划第二季度的总营业额要达到9100万元,设该公司5、6两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( )A、 B、 C、 D、5. 在平面直角坐标系中,把抛物线y=2x2绕原点旋转180°,再向右平移1个单位,向下平移2个单位,所得的抛物线的函数表达式为( )A、y=2(x﹣1)2﹣2 B、y=2(x+1)2﹣2 C、y=﹣2(x﹣1)2﹣2 D、y=﹣2(x+1)2﹣26. 三角形两边长分别是8和6,第三边长是一元二次方程一个实数根,则该三角形的面积是( )A、24 B、48 C、24或 D、二、填空题
-
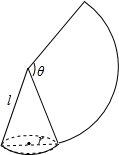
7. 分解因式:2a3﹣8a= .8. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角 ,则该圆锥的母线长 为 .
 9. 已知二次函数y=a(x+3)2-b(a≠0)有最大值1,则该函数图象的顶点坐标为 .10. 如图,C、D是AB为直径的半圆O上的点,若∠BAD=50°,则∠BCD=.
9. 已知二次函数y=a(x+3)2-b(a≠0)有最大值1,则该函数图象的顶点坐标为 .10. 如图,C、D是AB为直径的半圆O上的点,若∠BAD=50°,则∠BCD=. 11. 如图, 为 的直径,弦 于点E,已知 , ,则 的半径为.
11. 如图, 为 的直径,弦 于点E,已知 , ,则 的半径为. 12. 矩形纸片 ,长 ,宽 ,折叠纸片,使折痕经过点B,交 边于点E,点A落在点 处,展平后得到折痕 ,同时得到线段 , ,不再添加其它线段,当图中存在 角时, 的长为厘米.
12. 矩形纸片 ,长 ,宽 ,折叠纸片,使折痕经过点B,交 边于点E,点A落在点 处,展平后得到折痕 ,同时得到线段 , ,不再添加其它线段,当图中存在 角时, 的长为厘米.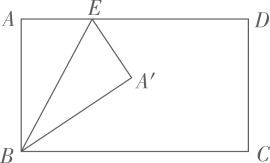
三、解答题
-
13. 解方程:(1)、x2-3x+1=0;(2)、(x+1)(x+2)=2x+4.14. 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1 .
 (1)、画出旋转后的图形;(2)、点A1的坐标为;(3)、在旋转过程中,点B经过的路径为弧BB1 , 那么弧BB1的长为多少?15. 已知内接于 , 请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出的平分线(保留作图痕迹,不写作法).
(1)、画出旋转后的图形;(2)、点A1的坐标为;(3)、在旋转过程中,点B经过的路径为弧BB1 , 那么弧BB1的长为多少?15. 已知内接于 , 请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出的平分线(保留作图痕迹,不写作法).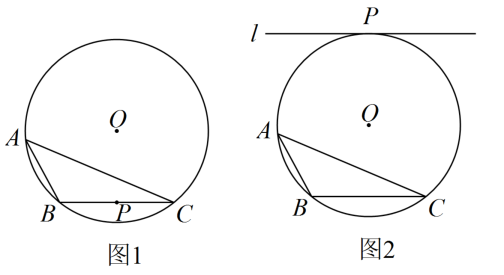 (1)、如图1,P是边的中点;(2)、如图2,直线l与相切于点P,且 .16. 小源的父母决定期末考试后带她去旅游,初步商量有意向的四个景点分别为: A.明月山, B.庐山, C.婺源, D.三清山.由于受到时间限制,只能选两个景点,于是小源的父母决定通过抽签选择,用四张小纸条分别写上四个景点做成四个签(外表无任何不同),让小源随机抽两次,每次抽一个签,每个签抽到的机会相等.(1)、小源最希望去婺源,则小源第一次恰好抽到婺源的概率是;(2)、除婺源外,小源还希望去明月山,求小源抽到婺源、明月山两个景点中至少一个的概率是多少.(通过“画树状图”或“列表”进行分析).17. 大余县某学校为了加强“五项管理”,调研了学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.
(1)、如图1,P是边的中点;(2)、如图2,直线l与相切于点P,且 .16. 小源的父母决定期末考试后带她去旅游,初步商量有意向的四个景点分别为: A.明月山, B.庐山, C.婺源, D.三清山.由于受到时间限制,只能选两个景点,于是小源的父母决定通过抽签选择,用四张小纸条分别写上四个景点做成四个签(外表无任何不同),让小源随机抽两次,每次抽一个签,每个签抽到的机会相等.(1)、小源最希望去婺源,则小源第一次恰好抽到婺源的概率是;(2)、除婺源外,小源还希望去明月山,求小源抽到婺源、明月山两个景点中至少一个的概率是多少.(通过“画树状图”或“列表”进行分析).17. 大余县某学校为了加强“五项管理”,调研了学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.
根据以上信息解答下列问题:
(1)、回收的问卷数为份,“严加干涉”部分对应扇形的圆心角度数为;(2)、把条形统计图补充完整;(3)、若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?18. 某商品市场销售抢手,其进价为每件80元,售价为每件130元,每个月可卖出500件;据市场调查,若每件商品的售价每上涨1元,则每个月少卖2件(每件售价不能高于240元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.(1)、求y与x的函数关系式,并直接写出自变量x的取值范围;(2)、每件商品的涨价多少元时,每个月可获得最大利润?最大的月利润是多少元?(3)、每件商品的涨价多少元时,每个月的利润恰为40000元?根据以上结论,请你直接写出x在什么范围时,每个月的利润不低于40000元?19. 如图,点B、C、D都在半径为4的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.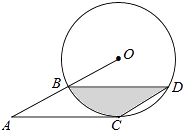 (1)、求证:AC是⊙O的切线;(2)、求弦BD的长.20. 在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
(1)、求证:AC是⊙O的切线;(2)、求弦BD的长.20. 在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.销售量y(千克)
…
34.8
32
29.6
28
…
售价x(元/千克)
…
22.6
24
25.2
26
…
(1)、某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)、如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
21. 如图, 与 的AC边相切于点C , 与AB、BC边分别交于点D、E , ,CE是 的直径.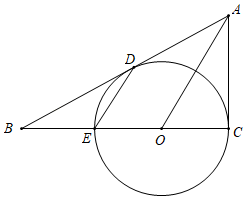 (1)、求证:AB是 的切线;(2)、若 求AC的长.22. 如图,直线y=x﹣3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=﹣x2+mx+n与x轴的另一个交点为A,顶点为P.
(1)、求证:AB是 的切线;(2)、若 求AC的长.22. 如图,直线y=x﹣3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=﹣x2+mx+n与x轴的另一个交点为A,顶点为P.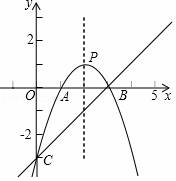 (1)、求3m+n的值;(2)、在该抛物线的对称轴上是否存在点Q,使以C,P,Q为顶点的三角形为等腰三角形?若存在,求出有符合条件的点Q的坐标;若不存在,请说明理由.(3)、将该抛物线在x轴上方的部分沿x轴向下翻折,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M“形状的新图象,若直线y=x+b与该“M”形状的图象部分恰好有三个公共点,求b的值.23. 已知∠α的顶点在正n边形的中心点O处,∠α绕着顶点O旋转,角的两边与正n边 形的两边分别交于点M、N,∠α与正n边形重叠部分面积为S.(1)、当n=4,边长为2,∠α=90°时,如图(1),请直接写出S的值;
(1)、求3m+n的值;(2)、在该抛物线的对称轴上是否存在点Q,使以C,P,Q为顶点的三角形为等腰三角形?若存在,求出有符合条件的点Q的坐标;若不存在,请说明理由.(3)、将该抛物线在x轴上方的部分沿x轴向下翻折,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M“形状的新图象,若直线y=x+b与该“M”形状的图象部分恰好有三个公共点,求b的值.23. 已知∠α的顶点在正n边形的中心点O处,∠α绕着顶点O旋转,角的两边与正n边 形的两边分别交于点M、N,∠α与正n边形重叠部分面积为S.(1)、当n=4,边长为2,∠α=90°时,如图(1),请直接写出S的值; (2)、当n=5,∠α=72°时,如图(2),请问在旋转过程中,S是否发生变化?并说明理由;
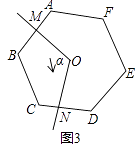
(2)、当n=5,∠α=72°时,如图(2),请问在旋转过程中,S是否发生变化?并说明理由;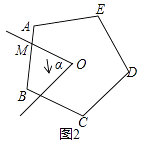 (3)、当n=6,∠α=120°时,如图(3),请猜想S是原正六边形面积的几分之几(不必说明理由).若∠α的平分线与BC边交于点P,判断四边形OMPN的形状,并说明理由.
(3)、当n=6,∠α=120°时,如图(3),请猜想S是原正六边形面积的几分之几(不必说明理由).若∠α的平分线与BC边交于点P,判断四边形OMPN的形状,并说明理由.