江西省赣州地区2021-2022学年九年级上学期期末质量检测数学试题

试卷更新日期：2022-11-07 类型：期末考试

进入出卷网下载

一、单选题

1. 方程3x²－2x－1＝0的二次项系数和一次项系数分别为（）

A、3和2 B、3和－2 C、3和－1 D、3和1

查看试题解析
2. 下面四个图形，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 不透明袋子中有 $1$ 个红球和 $2$ 个绿球，这些球除颜色外无其他差别．从袋子中随机取出 $1$ 个球，恰好是红球的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $1$

查看试题解析
4. 如图， $△ A B C$ 的三个顶点都在方格纸的格点上，其中 $A$ 点的坐标是 $(- 1 ， 0)$ ，现将 $△ A B C$ 绕 $A$ 点按逆时针方向旋转 $90 °$ ，则旋转后点 $C$ 的坐标是（）

A、 $(2 ， - 3)$ B、 $(- 2 ， 3)$ C、 $(- 2 ， 2)$ D、 $(- 3 ， 2)$

查看试题解析
5. 如图，AB是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点E， $C D = 2 O E$ ，则 $∠ B C D$ 的度数为（）

A、 $15 °$ B、 $22.5 °$ C、 $30 °$ D、 $45 °$

查看试题解析
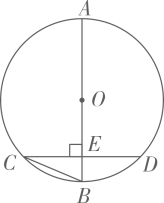6. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则下列结论中错误的是（）

A、 $a b c > 0$ B、函数的最大值为 $a - b + c$ C、当 $- 3 ⩽ x ⩽ 1$ 时， $y ⩾ 0$ D、 $4 a - 2 b + c < 0$

查看试题解析

二、填空题

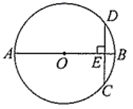
7. 若关于x的一元二次方程 $x^{2} - 3 x + a = 0$ 有一个根为1，则a的值为．

查看试题解析
8. 如图， $A B$ 为 $⊙ O$ 的直径， $A B = 10$ ， $C D$ 是弦， $A B ⊥ C D$ 于点 $E$ ，若 $C D = 6$ ，则 $E B =$ ．

查看试题解析
9. 点 $M (2 ， - 3)$ 关于原点对称的点的坐标是．

查看试题解析
10. 若一个扇形的半径为3，圆心角是120°，则它的面积是．

查看试题解析
11. 在平面直角坐标系 $x O y$ 中，若抛物线 $y = x^{2} + 2 x + k$ 与x轴只有一个交点，则 $k =$ .

查看试题解析
12. 如图，菱形ABCD中， $A B = 2$ ， $∠ A = 120 °$ ， E、F分别是AB、BC的中点，若点P从点E出发，沿 $E \to A \to D \to C$ 的路线运动，则当 $∠ E P F = 30 °$ 时，EP的长为．

查看试题解析

三、解答题

13. 解方程：

(1)、 $x^{2} - 4 x + 3 = 0$ ；

(2)、 $2 x^{2} - 5 x - 2 = 0$ ．

查看试题解析
14. 图，在每个小正方形的边长为1个单位的网格中， $△ A B C$ 的顶点均在格点（网格线的交点）上．

（ 1 ）将 $△ A B C$ 向右平移5个单位得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ；

（ 2 ）将（1）中的 $△ A_{1} B_{1} C_{1}$ 绕点C₁逆时针旋转 $90 °$ 得到 $△ A_{2} B_{2} C_{1}$ ，画出 $△ A_{2} B_{2} C_{1}$ ．

查看试题解析
15. 如图， $\overset{⌢}{A B}$ 的半径OA=2，OC⊥AB于点C，∠AOC＝60°．

(1)、求弦AB的长．

(2)、求 $\overset{⌢}{A B}$ 的长．

查看试题解析
16. 如图，△ABC是⊙O的内接三角形，∠ABC＝45°，请用无刻度的直尺按要求作图.

(1)、如图1，请在图1中画出弦CD，使得CD＝AC．

(2)、如图2，AB是⊙O的直径，AN是⊙O的切线，点B，C，N在同一条直线上请在图中画出△ABN的边AN上的中线BD．

查看试题解析
17. 即将举行的2022年杭州亚运会吉祥物“宸宸”、“琮琮”、“莲莲”：

将三张正面分别印有以上3个吉祥物图案的卡片（卡片的形状、大小、质地都相同)背面朝上、洗匀.

(1)、若从中任意抽取1张，抽得得卡片上的图案恰好为“莲莲”的概率是.

(2)、若先从中任意抽取1张，记录后放回，洗匀，再从中任意抽取1张，求两次抽取的卡片图案相同的概率.(请用树状图或列表的方法求解)

查看试题解析
18. 如图，⊙O的半径为1，点A是⊙O的直径BD延长线上的一点，C为⊙O上的一点， $A D = C D$ ， $∠ A = 30 °$ ．

(1)、求证：直线AC是⊙O的切线：

(2)、求 $△ A B C$ 的面积．

查看试题解析
19. 二次函数y＝ax²+bx+c（a≠0）的图象经过（3，0）点，当x＝1时，函数的最小值为-4．

(1)、求该二次函数的解析式并画出它的图象；

(2)、直线x＝m与抛物线y＝ax²+bx+c（a≠0）和直线y＝x-3的交点分别为点C，点D，点C位于点D的上方，结合函数的图象直接写出m的取值范围．

查看试题解析
20. 已知关于 $x$ 的方程 $x^{2} + 2 x + k - 4 = 0$ ．

(1)、如果方程有两个不相等的实数根，求 $k$ 的取值范围；

(2)、若 $k = 1$ ，求该方程的根．

查看试题解析
21. 今年以来，我市接待的游客人数逐月增加，据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人．

(1)、求四月和五月这两个月中，该景区游客人数平均每月增长百分之几；

(2)、若该景区仅有 $A ， B$ 两个景点，售票处出示的三种购票方式如表所示：
购票方式
甲
乙
丙
可游玩景点
A
B
A和B
门票价格
100元/人
80元/人
160元/人
据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万．并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票．
①若丙种门票价格下降10元，求景区六月份的门票总收入；
②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

查看试题解析
22. 如图1，对角线互相垂直的四边形叫做垂美四边形．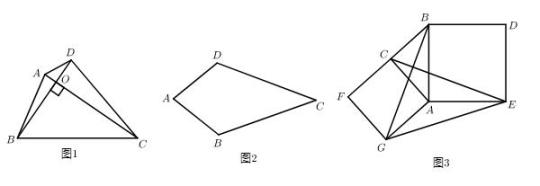

(1)、概念理解：如图2，在四边形 $A B C D$ 中， $A B = A D$ ， $C B = C D$ ，问四边形 $A B C D$ 是垂美四边形吗？请说明理由；

(2)、性质探究：如图1，垂美四边形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点O．猜想： $A B^{2} + C D^{2}$ 与 $A D^{2} + B C^{2}$ 有什么关系？并证明你的猜想．

(3)、解决问题：如图3，分别以 $R t △ A C B$ 的直角边 $A C$ 和斜边 $A B$ 为边向外作正方形 $A C F G$ 和正方形 $A B D E$ ，连结 $C E$ ， $B G$ ， $G E$ ．已知 $A C = 4$ ， $A B = 5$ ，求 $G E$ 的长．

查看试题解析
23. 如图，已知抛物线 $L ： y = x^{2} + b x + c$ 经过点 $A (0 ， - 5) ， B (5 ， 0)$ .

(1)、求 $b ， c$ 的值；

(2)、连结 $A B$ ，交抛物线L的对称轴于点M.
①求点M的坐标；

②将抛物线L向左平移 $m (m > 0)$ 个单位得到抛物线 $L_{1}$ .过点M作 $M N / / y$ 轴，交抛物线 $L_{1}$ 于点N.P是抛物线 $L_{1}$ 上一点，横坐标为 $- 1$ ，过点P作 $P E / / x$ 轴，交抛物线L于点E，点E在抛物线L对称轴的右侧.若 $P E + M N = 10$ ，求m的值.

查看试题解析

购票方式	甲	乙	丙
可游玩景点	A	B	A和B
门票价格	100元/人	80元/人	160元/人