江西省抚州市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-07 类型:期末考试
一、单选题
-
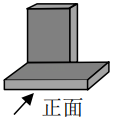
1. 方程x2=x的解是( )A、x=1 B、x=0 C、x1=1,x2=0 D、x1=﹣1,x2=02. 两个完全相同的长方体,按如图方式摆放,其主视图为( )
 A、
A、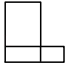 B、
B、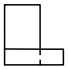 C、
C、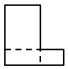 D、
D、 3. 如图,点A、B、C均在4x4的正方形网格的格点上,则tan∠BAC=( )
3. 如图,点A、B、C均在4x4的正方形网格的格点上,则tan∠BAC=( ) A、 B、 C、 D、4. 在两个不透明的口袋中,各自装有编号为1,2,3的三个球,球除编号外无其他区别,则在两个口袋中各取一个球,两球上的编号的和为偶数的概率为( )A、 B、 C、 D、5. 如图,在▱ABCD中,对角线BD⊥AD,AB=16,∠A=60°,O为BD的中点,E为边AB上一动点,以2cm/s的速度从A点向B点运动,运动时间为ts,连接EO并延长交CD于点F,连接DE、BF,下列结论不成立的是( )
A、 B、 C、 D、4. 在两个不透明的口袋中,各自装有编号为1,2,3的三个球,球除编号外无其他区别,则在两个口袋中各取一个球,两球上的编号的和为偶数的概率为( )A、 B、 C、 D、5. 如图,在▱ABCD中,对角线BD⊥AD,AB=16,∠A=60°,O为BD的中点,E为边AB上一动点,以2cm/s的速度从A点向B点运动,运动时间为ts,连接EO并延长交CD于点F,连接DE、BF,下列结论不成立的是( ) A、四边形DEBF为平行四边形 B、若t=4,则四边形DEBF为菱形 C、若t=2,则四边形DEBF为矩形 D、若t=6,则四边形DEBF为正方形6. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,与x轴的一个交点为(3,0),对称轴为直线x=1,有下列四个结论:①abc>0;②2a+b=0;③当x>1时,y随x的增大而减小;④3a+c=0,其中正确的结论个数有( )
A、四边形DEBF为平行四边形 B、若t=4,则四边形DEBF为菱形 C、若t=2,则四边形DEBF为矩形 D、若t=6,则四边形DEBF为正方形6. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,与x轴的一个交点为(3,0),对称轴为直线x=1,有下列四个结论:①abc>0;②2a+b=0;③当x>1时,y随x的增大而减小;④3a+c=0,其中正确的结论个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 若关于x的一元二次方程x2-2021x+c=0的一个根为-1,则另一个根为 .8. 已知二次函数的图象开口向下,顶点坐标是(0,3),则这个二次函数的表达式可以是 .9. 如图,正方形ABCD,AB=4,E、F点分别是CD、AD边上的点,AE与BF相交于点H,AF=DE=1,G点是BE上的中点,则GH的长为 .
 10. 如图,将一块等腰直角三角板的一条直角边BC放置在x轴上,反比例函数y=的图象经过点A(2,6),交斜边AC于E点,则E点的坐标为 .
10. 如图,将一块等腰直角三角板的一条直角边BC放置在x轴上,反比例函数y=的图象经过点A(2,6),交斜边AC于E点,则E点的坐标为 . 11. 如图,在平面直角坐标系中,菱形ABCD的一边AB在x轴上,顶点B在x轴正半轴上.若抛物线y=x2-5x+4经过点C、D,则点B的坐标为 .
11. 如图,在平面直角坐标系中,菱形ABCD的一边AB在x轴上,顶点B在x轴正半轴上.若抛物线y=x2-5x+4经过点C、D,则点B的坐标为 . 12. 如图,已知直线与x轴交于点B,与y轴交于点A,点P为直线AB上一动点(不与A、B重合),过点P作PQ⊥x轴于点Q,若以点P,O,Q为顶点的三角形与△AOB相似,则点P的坐标为 .
12. 如图,已知直线与x轴交于点B,与y轴交于点A,点P为直线AB上一动点(不与A、B重合),过点P作PQ⊥x轴于点Q,若以点P,O,Q为顶点的三角形与△AOB相似,则点P的坐标为 .
三、解答题
-
13.(1)、计算:2sin30°-tan45°.(2)、用适当的方法解一元二次方程:x2-2x-1=0.14. 已知 , 且a+3b-2c=15,求a+b-c的值.15. 已知关于x的一元二次方程x2-6x+m-3=0的两个根为a,b.(1)、若a,b分别为矩形的两条对角线的长,求m的值;(2)、若a,b分别是菱形的两条对角线的长,且菱形的面积为4,求m的值.16. 如图,在平行四边形ABCD中,AB=4,BC=2,点F在BC的延长线上,AF与CD交于点E,且∠1=∠F,求CF和DE的长.
 17. 在如图中,A、B两点在反比例函数y=的图象上,AB过O点,△ABC是等边三角形,点D为AC的中点,请用无刻度的直尺按下列要求画图.
17. 在如图中,A、B两点在反比例函数y=的图象上,AB过O点,△ABC是等边三角形,点D为AC的中点,请用无刻度的直尺按下列要求画图. (1)、在图1中,在x轴上画出点F,使四边形ADBF为矩形;(2)、在图2中,画出菱形ACBF.18. 2021年1月以来,教育部相继出台文件,对加强中小学生手机、睡眠、读物、作业、体质“五项管理”作出部署.抚州市某中学积极响应教育部的号召,对本校“五项管理”落实情况进行抽查,各年级分别抽查一项不同的管理项目.(1)、若先抽查九年级,则选到“作业”这项管理检查的概率是;(2)、若先抽查九年级,恰好选到“作业”,用画树状图或列表的方法求七年级和八年级选到“手机”和“体质”两项管理的概率.19. 已知二次函数y=ax2+2x+c的图象经过点(1,4)和(0,3)两点,与x轴交于A、B两点(A点在B点的左侧).(1)、求二次函数的表达式及对称轴;(2)、若点P在此抛物线上,且在x轴上方,求△PAB的最大面积.20. 如图1是一种建筑行业用的小型吊机实物图,图2,图3是吊机的示意图,支架AB=150cm,吊杆AM=200cm,∠ACB=90°,∠BAC=37°
(1)、在图1中,在x轴上画出点F,使四边形ADBF为矩形;(2)、在图2中,画出菱形ACBF.18. 2021年1月以来,教育部相继出台文件,对加强中小学生手机、睡眠、读物、作业、体质“五项管理”作出部署.抚州市某中学积极响应教育部的号召,对本校“五项管理”落实情况进行抽查,各年级分别抽查一项不同的管理项目.(1)、若先抽查九年级,则选到“作业”这项管理检查的概率是;(2)、若先抽查九年级,恰好选到“作业”,用画树状图或列表的方法求七年级和八年级选到“手机”和“体质”两项管理的概率.19. 已知二次函数y=ax2+2x+c的图象经过点(1,4)和(0,3)两点,与x轴交于A、B两点(A点在B点的左侧).(1)、求二次函数的表达式及对称轴;(2)、若点P在此抛物线上,且在x轴上方,求△PAB的最大面积.20. 如图1是一种建筑行业用的小型吊机实物图,图2,图3是吊机的示意图,支架AB=150cm,吊杆AM=200cm,∠ACB=90°,∠BAC=37° (1)、如图2,若AM⊥AB,求点M到地平面BC的距离;(2)、如图3,当液压杆DE伸长时,此时点M比(1)中的点M到地平面BC的距离升高了21cm,求∠MAB的度数.(参考数据:sin37°≈0.6,cos37°≈0.8,sin45°≈0.7)21. 如图,甲地、乙地分别是馨雨和馨望两家的自留地,他们两家都用来种西瓜,两块地的四周都是宽度相同的田埂,甲地的面积是240m2 .
(1)、如图2,若AM⊥AB,求点M到地平面BC的距离;(2)、如图3,当液压杆DE伸长时,此时点M比(1)中的点M到地平面BC的距离升高了21cm,求∠MAB的度数.(参考数据:sin37°≈0.6,cos37°≈0.8,sin45°≈0.7)21. 如图,甲地、乙地分别是馨雨和馨望两家的自留地,他们两家都用来种西瓜,两块地的四周都是宽度相同的田埂,甲地的面积是240m2 . (1)、若馨望家的地比馨雨家的地多了50%,则馨望家地的面积是m2;(2)、在(1)的条件下,求田埂的宽度.(3)、若馨雨家今年收获了800斤西瓜,种西瓜的成本是0.5元/斤,若以2元/斤进行销售,每天可销售40斤西瓜,经调查发现:每斤西瓜降价0.1元,每天就可多销售10斤西瓜,为了每天获利90元,且售价不得低于1.5元/斤,问售完所有的西瓜,馨雨家能赚多少元?22. 如图,反比例函数y=(x>0)的图象上的A点与反比例函数y=(x<0)的图象上的B点关于原点O对应(AB经过原点O),且OB=2OA,我们称反比例函数y=(x<0)是反比例函数y=(x>0)的“位似反比例函数”,其中O为位似中心.
(1)、若馨望家的地比馨雨家的地多了50%,则馨望家地的面积是m2;(2)、在(1)的条件下,求田埂的宽度.(3)、若馨雨家今年收获了800斤西瓜,种西瓜的成本是0.5元/斤,若以2元/斤进行销售,每天可销售40斤西瓜,经调查发现:每斤西瓜降价0.1元,每天就可多销售10斤西瓜,为了每天获利90元,且售价不得低于1.5元/斤,问售完所有的西瓜,馨雨家能赚多少元?22. 如图,反比例函数y=(x>0)的图象上的A点与反比例函数y=(x<0)的图象上的B点关于原点O对应(AB经过原点O),且OB=2OA,我们称反比例函数y=(x<0)是反比例函数y=(x>0)的“位似反比例函数”,其中O为位似中心. (1)、反比例函数y=(x<0)反比例函数y=(x>0)的“位似反比例函数”;(填“是”或“不是”)(2)、若反比例函数y=(x>0)的图象过点A(1,4).
(1)、反比例函数y=(x<0)反比例函数y=(x>0)的“位似反比例函数”;(填“是”或“不是”)(2)、若反比例函数y=(x>0)的图象过点A(1,4).①则m的值为;
②若A2022在反比例函数y=(x>0)的图象上,对应点B2022在“位似反比例函数”y=(x<0)的图象上,求证:BB2022=2AA2022;
(3)、在(2)的条件下,在x轴的正半轴上是否存在一点P,使△ABP为直角三角形,若存在,求出P点的坐标.23. (1)、问题探究:在图1和图2中,ABCD,AD⊥BC于点O.
(1)、问题探究:在图1和图2中,ABCD,AD⊥BC于点O.①如图1,若点O是BC的中点,AD=6,BC=8,则AD2= , BC2= , (AB+CD)2=;
②如图2,AO:DO=1:3,AO=3,BO=4,则AD2= , BC2= , (AB+CD)2=;
(2)、请你观察(1)中的计算结果,猜想AD2 , BC2 , (AB+CD)2三者之间的关系.(3)、归纳证明:请利用图2证明你发现的关系式;
(4)、应用结论:如图3,在矩形ABCD中,E,F两点均在AD边上,BE⊥CF交于G点,EF:BE=1:4,CF=3,BC=4.求证:CG=CD;
(5)、拓展应用:如图4,已知BD为△ABC的中线,CE⊥BD交AB于点E,交BD于点F,AE=5,BD=10,EC=15,求BC的长.