2022年秋季北师版数学九年级上册期末复习检测A
试卷更新日期:2022-11-05 类型:期末考试
一、单选题(每题3分,共30分)
-
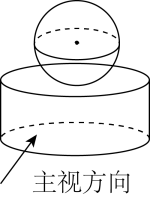
1. 某几何体如图所示,它的俯视图是( )
 A、
A、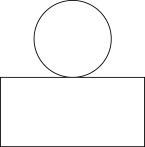 B、
B、 C、
C、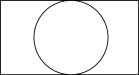 D、
D、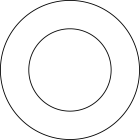 2. 已知 , ,若 ,则 ( )A、4 B、6 C、8 D、163. 为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )A、 B、 C、 D、4. 如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中错误的是( )
2. 已知 , ,若 ,则 ( )A、4 B、6 C、8 D、163. 为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )A、 B、 C、 D、4. 如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中错误的是( ) A、AB=AD B、AC⊥BD C、AC=BD D、∠DAC=∠BAC5. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )
A、AB=AD B、AC⊥BD C、AC=BD D、∠DAC=∠BAC5. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )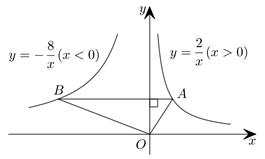 A、3 B、5 C、6 D、106. 一元二次方程的解是( )A、 B、 C、 D、7. 已知△ABC与△A1B1C1是位似图形,位似比是1:3,则△ABC与△A1B1C1的面积比( )A、1 :3 B、1:6 C、1:9 D、3:18. 若关于x的一元二次方程有两个实数根 , , 且 , 则( )A、2或6 B、2或8 C、2 D、69. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )
A、3 B、5 C、6 D、106. 一元二次方程的解是( )A、 B、 C、 D、7. 已知△ABC与△A1B1C1是位似图形,位似比是1:3,则△ABC与△A1B1C1的面积比( )A、1 :3 B、1:6 C、1:9 D、3:18. 若关于x的一元二次方程有两个实数根 , , 且 , 则( )A、2或6 B、2或8 C、2 D、69. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )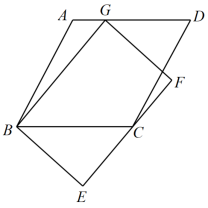 A、 B、 C、 D、310. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )
A、 B、 C、 D、310. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )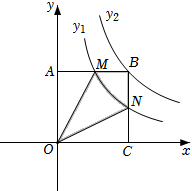 A、3 B、-3 C、 D、
A、3 B、-3 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,反比例函数的图象经过矩形对角线的交点E和点A,点B、C在x轴上,的面积为6,则 .
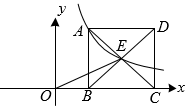 12. 已知x1、x2是关于x的方程x2﹣2x+k﹣1=0的两实数根,且=x12+2x2﹣1,则k的值为 .13. 如图,A是双曲线上的一点,点C是OA的中点,过点C作y轴的垂线,垂足为D,交双曲线于点B,则△ABD的面积是 .
12. 已知x1、x2是关于x的方程x2﹣2x+k﹣1=0的两实数根,且=x12+2x2﹣1,则k的值为 .13. 如图,A是双曲线上的一点,点C是OA的中点,过点C作y轴的垂线,垂足为D,交双曲线于点B,则△ABD的面积是 .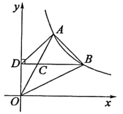 14. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .
14. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .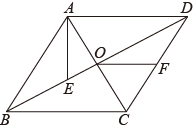 15. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.
15. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.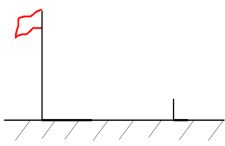 16. 已知是直角三角形,连接以为底作直角三角形且是边上的一点,连接和且则长为 .
16. 已知是直角三角形,连接以为底作直角三角形且是边上的一点,连接和且则长为 .
三、解答题(共8题,共72分)
-
17. 如图,在菱形中,对角线 , 相交于点 , 点 , 在对角线上,且 , .
求证:四边形是正方形.
 18. 为扎实推进“五育并举”工作,某校利用课外活动时间开设了舞蹈、篮球、围棋和足球四个社团活动,每个学生只选择一项活动参加.为了解活动开展情况,学校随机抽取部分学生进行调查,将调查结果绘成如下表格和扇形统计图.
18. 为扎实推进“五育并举”工作,某校利用课外活动时间开设了舞蹈、篮球、围棋和足球四个社团活动,每个学生只选择一项活动参加.为了解活动开展情况,学校随机抽取部分学生进行调查,将调查结果绘成如下表格和扇形统计图.参加四个社团活动人数统计表
社团活动
舞蹈
篮球
围棋
足球
人数
50
30
80
参加四个社团活动人数扇形统计图

请根据以上信息,回答下列问题:
(1)、抽取的学生共有人,其中参加围棋社的有人;(2)、若该校有3200人,估计全校参加篮球社的学生有多少人?(3)、某班有3男2女共5名学生参加足球社,现从中随机抽取2名学生参加学校足球队,请用树状图或列表法说明恰好抽到一男一女的概率.19. 如图,▱ABCD中,E为BC边的中点,连接AE并延长交DC的延长线于点F,延长EC至点G,使CG=CE,连接DG、DE、FG.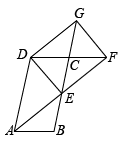 (1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.20.
(1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.20.如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1 .
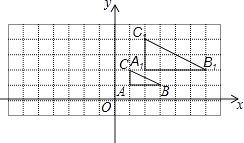 (1)、△A1B1C1与△ABC的位似比是;(2)、画出△A1B1C1关于y轴对称的△A2B2C2;(3)、设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是 .21. 如图,已知一次函数y=ax+b与反比例函数y=(x<0)的图像交于A(﹣2,4),B(﹣4,2)两点,且与x轴和y轴分别交于点C、点D.
(1)、△A1B1C1与△ABC的位似比是;(2)、画出△A1B1C1关于y轴对称的△A2B2C2;(3)、设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是 .21. 如图,已知一次函数y=ax+b与反比例函数y=(x<0)的图像交于A(﹣2,4),B(﹣4,2)两点,且与x轴和y轴分别交于点C、点D.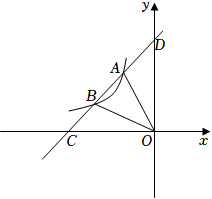 (1)、根据图像直接写出不等式<ax+b的解集;(2)、求反比例函数与一次函数的解析式;(3)、点P在y轴上,且S△AOP=S△AOB , 请求出点P的坐标.22. 2022北京冬奥会期间,某网店直接从工厂购进A、B两款冰嫩墩钥匙扣,进货价和销售价如下表:(注:利润=销售价-进货价)
(1)、根据图像直接写出不等式<ax+b的解集;(2)、求反比例函数与一次函数的解析式;(3)、点P在y轴上,且S△AOP=S△AOB , 请求出点P的坐标.22. 2022北京冬奥会期间,某网店直接从工厂购进A、B两款冰嫩墩钥匙扣,进货价和销售价如下表:(注:利润=销售价-进货价)类别
价格
A款钥匙扣
B款钥匙扣
进货价(元/件)
30
25
销售价(元/件)
45
37
(1)、网店第一次用850元购进A、B两款钥匙扣共30件,求两款钥匙扣分别购进的件数;(2)、第一次购进的冰墩嫩钥匙扣售完后,该网店计划再次购进A、B两款冰墩墩钥匙扣共80件(进货价和销售价都不变),且进货总价不高于2200元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?(3)、冬奥会临近结束时,网店打算把B款钥匙扣调价销售.如果按照原价销售,平均每天可售4件.经调查发现,每降价1元,平均每天可多售2件,将销售价定为每件多少元时,才能使B款钥匙扣平均每天销售利润为90元?23. 如图,一次函数的图像与反比例函数的图像交于点 , 与轴交于点 , 与轴交于点 , 轴于点 , , 点关于直线的对称点为点 .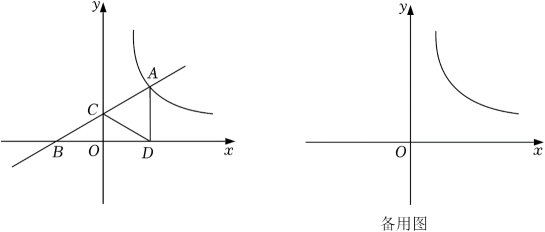 (1)、点是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.
(1)、点是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.①求、的值;
②若点在轴上,当最大时,求点的坐标.
24. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;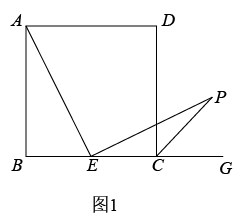
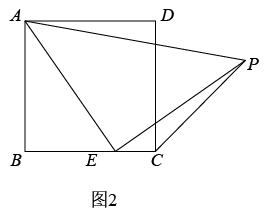
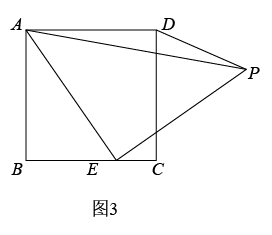 (1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.
(1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.