江西省宜春市丰城市2022-2023学年高二上学期数学10月期中考试试卷

试卷更新日期：2022-11-04 类型：期中考试

进入出卷网下载

一、单选题

1. 空间中垂直于同一条直线的两条直线（）

A、平行 B、相交 C、异面 D、以上均有可能

查看试题解析
2.
如图所示的直观图的平面图形ABCD是（　　）

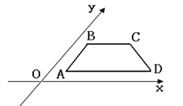A、任意梯形 B、直角梯形 C、任意四边形 D、平行四边形

查看试题解析
3. 若直线 $x + y + a = 0$ 平分圆 $x^{2} + y^{2} - 2 x + 4 y + 1 = 0$ ，则 $a$ 的值为（）

A、1 B、－1 C、2 D、－2

查看试题解析
4. 若直线 $l_{1} : x + a y + 6 = 0$ 与 $l_{2} : (a - 2) x + 3 y + 2 a = 0$ 平行，则 $l_{1}^{}$ 与 $l_{2}^{}$ 间的距离为（）

A、 $\sqrt{2}$ B、 $\frac{8 \sqrt{2}}{3}$ C、 $\sqrt{3}$ D、 $\frac{8 \sqrt{3}}{3}$

查看试题解析
5. 正方体的全面积是 $a^{2}$ ，它的顶点都在球面上，这个球的表面积是（）

A、 $\frac{π a^{2}}{3}$ B、 $\frac{π a^{2}}{2}$ C、 $2 π a^{2}$ D、 $3 π a^{2}$

查看试题解析
6. 已知圆 $x^{2} + y^{2} - 2 a x - 2 y + (a - 1)^{2} = 0$ $(0 < a < 1)$ ，则原点 $O$ 在（）

A、圆内 B、圆外 C、圆上 D、圆上或圆外

查看试题解析
7. 若直线 $l ： k x - y - 2 = 0$ 与曲线 $C ： \sqrt{1 - (y - 1)^{2}} = x - 1$ 有两个不同的交点，则实数 $k$ 的取值范围是（）

A、 $(\frac{4}{3} ， 2]$ B、 $(\frac{4}{3} ， 4)$ C、 $[- 2 ， - \frac{4}{3}) ∪ (\frac{4}{3} ， 2]$ D、 $(\frac{4}{3} ， + \infty)$

查看试题解析
8. 椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ 的焦点F₁ ， F₂ ，点P为其上的动点，当∠F₁PF₂为钝角时，点P横坐标的取值范围是（）

A、（﹣ $\frac{\sqrt{5}}{5}$ ， $\frac{\sqrt{5}}{5}$ ） B、（﹣ $\frac{2 \sqrt{5}}{5}$ ， $\frac{2 \sqrt{5}}{5}$ ） C、（﹣ $\frac{3 \sqrt{5}}{5}$ ， $\frac{3 \sqrt{5}}{5}$ ） D、（﹣ $\frac{6 \sqrt{5}}{5}$ ， $\frac{6 \sqrt{5}}{5}$ ）

查看试题解析

二、多选题

9. 直线 $y = k x - 1$ 与圆 $C ： (x + 3)^{2} + (y - 3)^{2} = 36$ 相交于A，B两点，则线段 $A B$ 的长度可能为（）

A、 $3 \sqrt{3}$ B、 $4 \sqrt{3}$ C、12 D、14

查看试题解析
10. 长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的长、宽、高分别为3，2，1，则（）

A、长方体的表面积为20 B、长方体的体积为6 C、沿长方体的表面从A到 $C_{1}$ 的最短距离为 $3 \sqrt{2}$ D、沿长方体的表面从A到 $C_{1}$ 的最短距离为 $2 \sqrt{5}$

查看试题解析
11. 已知直线l过点 $(3 ， 4)$ ，点 $A (- 2 ， 2)$ ， $B (4 ， - 2)$ 到l的距离相等，则l的方程可能是（）

A、 $x - 2 y + 2 = 0$ B、 $2 x - y - 2 = 0$ C、 $2 x + 3 y - 18 = 0$ D、 $2 x - 3 y + 6 = 0$

查看试题解析
12. 如图，矩形ABCD中， $A B = 2 A D = 2$ ， E为边AB的中点，将△ADE沿直线DE翻折成△A₁DE（点A不落在底面BCDE内），若M为线段A₁C的中点，则在△ADE翻转过程中，以下命题正确的是（）

A、四棱锥 $A_{1} - B C D E$ 体积最大值为 $\frac{\sqrt{2}}{4}$ B、线段BM长度是定值 C、MB∥平面A₁DE一定成立 D、存在某个位置，使 $D E ⊥ A_{1} C$

查看试题解析

三、填空题

13. 一个直角三角形的两条直角边的长分别为3cm和4cm，将这个直角三角形以斜边为轴旋转一周，所得旋转体的体积是 $c m^{3}$ .

查看试题解析
14. 设点 $A (m ， - m + 3) ， B (2 ， m - 1) ， C (- 1 ， 4)$ ，若直线 $A C$ 的斜率等于直线 $B C$ 的斜率的3倍，则实数m的值为.

查看试题解析
15. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 棱长为4. 若M是平面 $B C C_{1} B_{1}$ 内的动点，且 $A M ⊥ M C$ ，则 $A_{1} M$ 与平面 $B C C_{1} B_{1}$ 所成角的正切值的最大值为.

查看试题解析
16. 已知关于x的方程 $a s i n x + b c o s x = 2$ 有实数解，则 ${(a - 1)}^{2} + {(b - 1)}^{2}$ 最小值是．

查看试题解析

四、解答题

17. 如图，在四棱锥P—ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP=AB，BP=BC=2，E，F分别是PB，PC的中点.

(Ⅰ)证明：EF∥平面PAD；

(Ⅱ)求三棱锥E—ABC的体积V.

查看试题解析
18. 已知直线 $l_{1} ： (m + 2) x + m y - 8 = 0$ 与直线 $l_{2} ： m x + y - 4 = 0 ， m \in R$ ．

(1)、若 $l_{1} / / l_{2}$ ，求m的值；

(2)、若点 $P (1 ， m)$ 在直线 $l_{2}$ 上，直线 $l$ 过点P，且在两坐标轴上的截距之和为0，求直线 $l$ 的方程．

查看试题解析
19. 已知圆C过点 $M (0 ， - 2) ， N (3 ， 1)$ ，且圆心C在直线 $x + 2 y + 1 = 0$ 上．

(1)、求圆C的标准方程．

(2)、设直线 $a x - y + 1 = 0$ 与圆C交于不同的两点A，B，是否存在实数a，使得过点 $P (2 ， 0)$ 的直线l垂直平分弦AB？若存在，求出实数a的值；若不存在，请说明理由．

查看试题解析
20. 如图，在四棱锥P—ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE.

(1)、证明：BD⊥平面PAC；

(2)、若 $P A = A D = 2$ ，求二面角B—PC—A的正切值.

查看试题解析
21. 已知 $A (1 ， 0)$ ， $B (- 2 ， 3)$ ，动点P满足 $2 | P A | = | P B |$ ，动点P的轨迹为曲线C．

(1)、求曲线C的方程；

(2)、若直线 $l$ ： $(2 m + 1) x - (m - 1) y - m - 2 = 0$ 与曲线C交于M，N两点，求 $| M N |$ 的取值范围．

查看试题解析
22. 已知椭圆的 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a ＞ b ＞ 0)$ 的焦距为 $2 \sqrt{6}$ ，且过点 $A (2 ， 1)$ .

(1)、求椭圆 $C$ 的方程；

(2)、若不经过点 $A$ 的直线 $l ： y = k x + m$ 与 $C$ 交于 $P ， Q$ 两点，且直线 $A P$ 与直线 $A Q$ 的斜率之和为0，求 $k$ 的值.

查看试题解析