浙江省宁波市慈溪市2022-2023学年七年级上学期第一次月考数学试题

试卷更新日期：2022-11-04 类型：月考试卷

进入出卷网下载

一、单选题(每题3分，共30分)

1. $- \frac{1}{2}$ 的倒数是（）

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 在-7，5，0，-3这四个数中，绝对值最大的数是（）

A、-7 B、5 C、0 D、-3

查看试题解析
3. 在 $-$ 2.5 ， 100， 0.01， $- \frac{3}{2}$ 四个数中，最小的数是（）

A、 $-$ 2.5 B、100 C、0.01 D、 $- \frac{3}{2}$

查看试题解析
4. 下列计算正确的是（）

A、 $(- 6) - (+ 3) = 3$ B、 $(- 6) \times 3 = - 18$ C、 $(- 6) \div 3 = 2$ D、 $(- 6) + (- 3) = - 3$

查看试题解析
5. 一个点在数轴上移动时，它所对应的数，也会有相应的变化．若点A先从原点开始，先向右移动3个单位长度，再向左移动5个单位长度，这时该点所对应的数的相反数是（）

A、2 B、-2 C、8 D、-8

查看试题解析
6. 下列说法，正确的有（）
（1）整数和分数统称为有理数；（2）符号不同的两个数叫做互为相反数；（3）一个数的绝对值一定为正数；（4）最大的负数是-1．

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 已知有理数a，b所对应的点在数轴上的位置如图所示，则有（）

A、﹣b＜a＜0 B、﹣a＜0＜b C、a＜0＜﹣b D、0＜b＜﹣a

查看试题解析
8. 4个非零有理数相乘，积的符号是负号，则这4个有理数中，正数有（）

A、1个或3个 B、1个或2个 C、2个或4个 D、3个或4个

查看试题解析
9. 如果ab≠0，那么 $\frac{a}{|a|} + \frac{b}{|b|}$ 的值不可能是（）

A、0 B、1 C、2 D、-2

查看试题解析
10. 如图，正方形的周长为8个单位，在该正方形的四个顶点处分别标上0，2，4，6，先让正方形上表示数字6的点与数轴上表示-3的点重合，再将数轴按顺时针方向环绕在该正方形上，则数轴上表示2021的点与正方形上表示数字（）的点重合．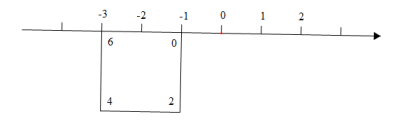

A、0 B、2 C、4 D、6

查看试题解析

二、填空题（每空4分，共24分）

11. 在数学知识抢答赛中，如果用 $+ 10$ 分表示得10分，那么扣20分表示为.

查看试题解析
12. 在数轴上表示 $4$ 与 $- 3$ 的两个点之间的距离是.

查看试题解析
13. 若a，b互为倒数，c，d互为相反数，则2c+2d-3a×b的值为．

查看试题解析
14. 绝对值小于4的所有整数的积为．

查看试题解析
15. 用 $[x]$ 表示不大于x的整数中的最大整数，如 $[2.4] = 2$ ， $[- 3.3] = - 4$ ，请计算 $[5.8] + [- 4.4]$ = ．

查看试题解析
16. 不为1的有理数，我们把 $\frac{1}{1 - a}$ 称为 $a$ 的差倒数．如： $3$ 的差倒数是 $\frac{1}{1 - 3} = - \frac{1}{2}$ ， $－ 1$ 的差倒数是 $\frac{1}{1 - (- 1)} = \frac{1}{2}$ ．已知 $a_{1} = 3$ ， $a_{2}$ 是 $a_{1}$ 的差倒数， $a_{3}$ 是 $a_{2}$ 的差倒数， $a_{4}$ 是 $a_{3}$ 的差倒数，…，依此类推，则 $a_{2021} =$ ．

查看试题解析

三、解答题（第17题8分，第18题8分，第19题6分，第20题8分，第21题10分，第22题8分，第23题10分，第24题8分，共66分）

17. 把下列各数填在相应的表示集合的大括号里．
4，0.5，-1 $\frac{1}{2}$ ， 10%，-5，-3.14，0， $\frac{1}{3}$ ， +2018

(1)、正整数集合（                                                     ）

(2)、分数集合（                                                     ）

(3)、负有理数集合（                                                   ）

(4)、整数集合（                                                     ）．

查看试题解析
18. 计算

(1)、 $（ - 3 ） + （ - 4 ） - （ + 11 ） - （ - 9 ）$

(2)、 $(\frac{5}{6} - \frac{2}{3} + \frac{3}{4}) \times (- 24)$

(3)、 $- 4 \div \frac{2}{3} - （ - \frac{2}{3} ） \times （ - 30 ）$

(4)、 $（ - 1.5 ） \times \frac{4}{5} \div (- \frac{2}{5}) \times \frac{3}{4}$

查看试题解析
19. 在数轴上画出表示下列各数的点，并按从小到大的顺序用“ $<$ ”连接上述各数.
3.5 ，－3.5 ， 0 ， 2 ，－2 ， -0.5

查看试题解析
20. 如图，小明有4张写着不同数的卡片，请你按照题目要求抽出卡片，完成下列问题．

(1)、从中取出2张卡片，使这2张卡片上数字的乘积最大，如何抽取？最大值是多少？

(2)、从中取出2张卡片，使这2张卡片上数字相除的商最小，如何抽取？最小值是多少？

查看试题解析

21. 第66路公交车沿东西方向行驶，如果把车站的起点记为O，向东行驶记为正，向西行驶记为负，其中一辆车从车站出发以后行驶的路程如下表（单位：km）：

序号	1	2	3	4	5	6	7
路程	$+ 5$	$- 3$	$+ 10$	$- 8$	$- 6$	$+ 12$	$- 10$

(1)、该车最后是否回到了车站？为什么？

(2)、该辆车离开出发点最远是多少千米？

(3)、若每千米耗油

0.2

升，每升油价是

7.5

元，则从O地出发到行驶结束收油费是多少元？

查看试题解析

22. 如图，A在数轴上所对应的数为-2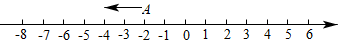

(1)、点B在点A右边，距离A点4个单位长度，则点B所对应的数是；

(2)、在（1）的条件下，点A以每秒2个单位长度沿数轴向左运动，同时点B以每秒2个单位长度沿数轴向右运动，当点A运动到-6所在的点处时，点B停止运动，此时A，B两点间距离是；

(3)、在（2）的条件下，现在A点静止不动，B点再以每秒2个单位长度沿数轴向左运动时，求经过多长时间A，B两点相距4个单位长度．

查看试题解析
23. 请你仔细阅读下列材料：计算：
$(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})$

解法 $1$ ：按常规方法计算

原式 $= (- \frac{1}{30}) \div [\frac{2}{3} + \frac{1}{6} - (\frac{1}{10} + \frac{2}{5})] = (- \frac{1}{30}) \div (\frac{5}{6} - \frac{1}{2}) = (- \frac{1}{30}) \times 3 = - \frac{1}{10}$

解法 $2$ ：简便计算，先求其倒数

原式的倒数为： $(\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \div (- \frac{1}{30}) = (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \times (- 30) = - 20 + 3 - 5 + 12 = - 10$

故 $(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) = - \frac{1}{10}$

再根据你对所提供材料的理解，模仿以上两种方法分别进行计算： $(- \frac{1}{56}) \div (\frac{3}{8} - \frac{3}{14} + \frac{1}{2} - \frac{2}{7})$

查看试题解析
24. 如图1，已知数轴上有三个点A，B，C，它们对应的数分别为 $a ， b ， c$ ，且 $c-b = b- a$ ，点C对应的数是10.

(1)、若BC=15，求 $a ， b 的值$
图1

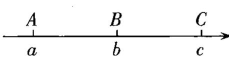(2)、如图2，在（1）的条件下，O为原点，动点P，Q分别从点A，C同时出发，点P向左运动，运动速度为每秒2个单位长度，点Q向右运动，运动速度为每秒1个单位长度，N为OP的中点，M为BQ的中点.
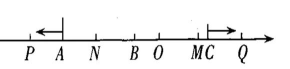图2

用含t的代数式表示PQ，MN.

在点P，Q的运动过程中，PQ与MN存在一个确定的等量关系，请指出它们之间的关系，并说明理由.

查看试题解析