浙江省金华市浦江县2022-2023学年七年级上学期数学10月检测试题
试卷更新日期:2022-11-04 类型:月考试卷
一、单选题 (本大题共 10 小题,共 30 分)
-
1. 9的相反数是( )A、-9 B、9 C、 D、2. 2021年5月18日上午,江苏省人民政府召开新闻发布会,公布了全省最新人口数据,其中连云港市的常住人口约为4600000人.把“4600000”用科学记数法表示为( )A、 B、 C、 D、3. 在 , , 1.62,0四个数中,有理数的个数为( )A、4 B、3 C、2 D、14. 有理数a,b,c,d在数轴上的对应点的位置如图所示. 若b+d=0,则下列结论正确的是( )
 A、b+c>0 B、>1 C、ad>bc D、|a|>|b|5. 已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.圆圆在该快递公司寄一件8千克的物品,需要付费( )A、17元 B、19元 C、21元 D、23元6. 如图,数轴上点A对应的数是 ,将点A沿数轴向左移动2个单位至点B,则点B对应的数是( )
A、b+c>0 B、>1 C、ad>bc D、|a|>|b|5. 已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.圆圆在该快递公司寄一件8千克的物品,需要付费( )A、17元 B、19元 C、21元 D、23元6. 如图,数轴上点A对应的数是 ,将点A沿数轴向左移动2个单位至点B,则点B对应的数是( )
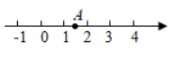 A、 B、-2 C、 D、7. 若 , , 且 , 则的值( )A、大于0 B、小于0 C、大于或等于0 D、小于或等于08. 观察下列算式:31=3 3 2=9 33=27 34=81 35=243 36=729…通过观察,用你所发现的规律得出32018的末位数是( )A、1 B、3 C、7 D、99. 按照如图所示的流程,若输出的 ,则输入的m为( )
A、 B、-2 C、 D、7. 若 , , 且 , 则的值( )A、大于0 B、小于0 C、大于或等于0 D、小于或等于08. 观察下列算式:31=3 3 2=9 33=27 34=81 35=243 36=729…通过观察,用你所发现的规律得出32018的末位数是( )A、1 B、3 C、7 D、99. 按照如图所示的流程,若输出的 ,则输入的m为( )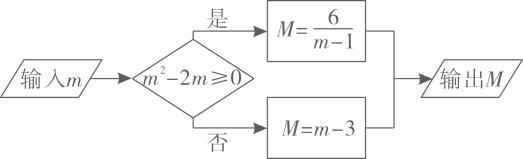 A、3 B、1 C、0 D、-110. 求的值,可令 , 则 , 因此 , 仿照以上推理,计算出的值为( )A、 B、 C、 D、
A、3 B、1 C、0 D、-110. 求的值,可令 , 则 , 因此 , 仿照以上推理,计算出的值为( )A、 B、 C、 D、二、填空题(每小题4分,共24分)
-
11. 如果盈利100元记作+100元,那么亏损50元记作元.12. 比较大小:(1)、-2
 (-2)
(-2) ; (2)、(-3)
; (2)、(-3)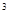 -3
-3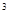 . 13. 若 与 互为相反数,则 的值为.14. 已知数轴上点表示7,点 , 表示互为相反数的两个数,且点与点间的距离为2,则点表示的数是.15. 某种商品每件的标价是330元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为 .16. 将一列有理数-1,2,-3,4,-5,6,……,按如图所示有序排列,
. 13. 若 与 互为相反数,则 的值为.14. 已知数轴上点表示7,点 , 表示互为相反数的两个数,且点与点间的距离为2,则点表示的数是.15. 某种商品每件的标价是330元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为 .16. 将一列有理数-1,2,-3,4,-5,6,……,按如图所示有序排列,
根据图中的排列规律可知,“峰1”中峰顶的位置(的位置)是有理数4,那么,
(1)、“峰6”中的位置是有理数;(2)、2008应排在、、、、中的位置.三、解答题 (本大题共8 大题,共66 分)
-
17. 把下列各数填在相应的大括号中:
-0.3, , 0,- , -6,0.25,-|-2|,-(-4)
正数集合{ …};
整数集合{ …}
分数集合{ …}.
18. 画出数轴并在数轴上描出表示下列各数的点,再用“”把这些数连接起来., 0,-1, , , 1.5.
19. 计算:(1)、 ;(2)、 .(3)、 ;(4)、(5)、 ;20. 已知 , 互为相反数, , 互为倒数,的绝对值是2,求的值.21. 某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示.(用正数表示上车的人数,负数表示下车的人数)
起点
A
B
C
D
终点
上车的人数
18
15
12
7
5
0
下车的人数
0
-3
-4
-10
-11
(1)、到终点下车还有 人;(2)、车行驶在那两站之间车上的乘客最多?站和 站;(3)、若每人乘坐一站需买票1元 , 问该车出车一次能收入多少钱?请列出算式并写出计算过程.22. 已知:数a,b,c在数轴上的对应点如图所示,
 (1)、在数轴上表示-a;(2)、比较大小(填“〈”或“〉”或“=”):a+b0,-3c0,c-a0;(3)、化简23. 概念学习
(1)、在数轴上表示-a;(2)、比较大小(填“〈”或“〉”或“=”):a+b0,-3c0,c-a0;(3)、化简23. 概念学习规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等.类比有理数的乘方,我们把2÷2÷2记作2③ , 读作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)记作(-3)④ , 读作“-3的圈4次方”,一般地,把(a≠0)记作aⓝ , 读作“a的圈n次方”.
初步探究
(1)、直接写出计算结果:2③= , ⑤=;(2)、深入思考
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
试一试:仿照右图的算式,将下列运算结果直接写成幂的形式.(-3)④=; 5⑥=; ⑩= .
(3)、想一想:将一个非零有理数a的圈n次方写成幂的形式等于;(4)、算一算:24÷23+(-16)×2④ .24. 数轴上点对应的数为-5,点在点右边,电子蚂蚁甲、乙在分别以2个单位秒、1个单位秒的速度向左运动,电子蚂蚁丙在以3个单位秒的速度向右运动. (1)、若电子蚂蚁丙经过秒运动到点,求点表示的数;(2)、若丙与甲同时出发,经过4秒后丙与甲相距5个单位长度,求点表示的数;(3)、若B点表示的数是15,设它们同时出发的时间为秒,是否存在的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出值;若不存在,说明理由.
(1)、若电子蚂蚁丙经过秒运动到点,求点表示的数;(2)、若丙与甲同时出发,经过4秒后丙与甲相距5个单位长度,求点表示的数;(3)、若B点表示的数是15,设它们同时出发的时间为秒,是否存在的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出值;若不存在,说明理由.