浙江省金华市浦江县2022-2023学年八年级上学期数学10月检测试题
试卷更新日期:2022-11-04 类型:月考试卷
一、选择题(每题3分,共30分)
-
1. 下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )A、13cm,12cm,20cm B、8cm,7cm,15cm C、5cm,5cm,11cm D、3cm,4cm,8cm2. 下列命题中,属于真命题的是( )A、同位角相等 B、角平分线上的点到角两边的距离相等 C、三角形的高线都在三角形内部 D、三个角对应相等的两个三角形全等3. 若a>b,则下列式子正确的是( )A、-2022a>-2022b B、a-2022>b-2022 C、2022-a>2022-b D、2022a<2022b4. 下列学习用具中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 不等式组的解集表示在数轴上正确的是( )A、
5. 不等式组的解集表示在数轴上正确的是( )A、 B、
B、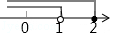 C、
C、 D、
D、 6. 不等式3(x-2)≤x+4的非负整数解有( )个A、4 B、5 C、6 D、无数7. 要证明命题“若a>b,则a2>b2”是假命题,下列a,b的值不能作为反例的是( )A、a=1,b=﹣2 B、a=0,b=﹣1 C、a=﹣1,b=﹣2 D、a=2,b=﹣18. 在Rt△ABC中,∠ABC=90°,AC=13,AB=12,则图中五个小直角三角形的周长之和为( )
6. 不等式3(x-2)≤x+4的非负整数解有( )个A、4 B、5 C、6 D、无数7. 要证明命题“若a>b,则a2>b2”是假命题,下列a,b的值不能作为反例的是( )A、a=1,b=﹣2 B、a=0,b=﹣1 C、a=﹣1,b=﹣2 D、a=2,b=﹣18. 在Rt△ABC中,∠ABC=90°,AC=13,AB=12,则图中五个小直角三角形的周长之和为( )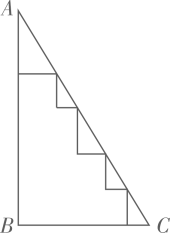 A、25 B、18 C、17 D、309. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A、25 B、18 C、17 D、309. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( ) A、CB=CD B、∠BCA=∠DCA C、∠BAC=∠DAC D、∠B=∠D=90°10. 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
A、CB=CD B、∠BCA=∠DCA C、∠BAC=∠DAC D、∠B=∠D=90°10. 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:①AE+BF=AB;②△DEF始终为等腰直角三角形;③S四边形CEDF=AB2;④AE2+CE2=2DF2 .
其中正确的是( )
 A、①②③④ B、①②③ C、①④ D、②③
A、①②③④ B、①②③ C、①④ D、②③二、填空题(每题4分,共24分)
-
11. “x的6倍减去8是正数”用不等式表示为 .12. 在△ABC中,AB=6,BC=8,则AC的长x的取值范围是。13. 不等式的最大整数解是 .14. 在等腰三角形中, 有两边长分别为6和8,则它的周长为。15. 以6和8为两条边的直角三角形斜边上的中线长为.16. 一副三角板按如图甲放置,其中, , , 斜边 , . 把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点 , 与D1E1相交于点F.那么 =度,线段AD1的长度是cm.

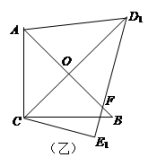
三、解答题(共66分)
-
17. 作图题

( 1 )尺规作图作出∠A的角平分线AD。
( 2 )尺规作图作出AC边上的中线BE。
(只要保留作图痕迹,不要求写作法和证明)
18. 如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数. 19. 解下列不等式(组):(1)、(2)、 .20. 如图是由16个小正方形组成的正方形网格图,现已将其中的两个涂黑.请你用四种不同的方法分别在下图中再涂黑三个空白的小正方形,使整个图形成为轴对称图形.
19. 解下列不等式(组):(1)、(2)、 .20. 如图是由16个小正方形组成的正方形网格图,现已将其中的两个涂黑.请你用四种不同的方法分别在下图中再涂黑三个空白的小正方形,使整个图形成为轴对称图形. 21. 如图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF,
21. 如图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF,
求证:
(1)、BC=EF(2)、△ABC≌△DEF(3)、AB∥DE22. 为了加强学生的交通安全意识,某中学和交警大队联合举行了“我当一日小交警”活动,星期天选派部分学生到交通路口值勤,协助交通警察维护交通秩序.若每一个路口安排4人,那么还剩下78人;若每个路口安排8人,那么最后一个路口不足8人,但不少于4人.求这个中学共选派值勤学生多少人?共有多少个交通路口安排值勤?23. 如图,已知:在△ABC中,AC=BC=8,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.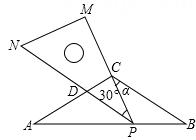 (1)、当PN∥BC时,判断△ACP的形状,并说明理由;(2)、点P在滑动时,当AP长为多少时,△ADP与△BPC全等,并说明理由;(3)、点P在滑动时,△PCD的形状可以是等腰三角形吗?若可以,
(1)、当PN∥BC时,判断△ACP的形状,并说明理由;(2)、点P在滑动时,当AP长为多少时,△ADP与△BPC全等,并说明理由;(3)、点P在滑动时,△PCD的形状可以是等腰三角形吗?若可以,请直接写出夹角α的大小; 若不可以,请说明理由.
24. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设运动时间为t秒. (1)、动点P运动2秒后,求△ABP的周长.(2)、问t满足什么条件时,△BCP为直角三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
(1)、动点P运动2秒后,求△ABP的周长.(2)、问t满足什么条件时,△BCP为直角三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?