浙江省温州市七校2022-2023学年九年级上学期期中联考数学试卷

试卷更新日期：2022-11-04 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题4分，共40分.）

1. 若 $\frac{a}{2}$ ＝ $\frac{b}{3}$ ，则 $\frac{b}{a + b}$ 的值是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{5}{3}$ D、 $\frac{3}{5}$

查看试题解析
2. 二次函数y＝x²﹣x﹣2的图形与y轴的交点坐标为（）

A、（﹣1，0） B、（2，0） C、（0，﹣2） D、（0，2）

查看试题解析
3. 若抛物线y＝ax²﹣2x+3经过点P（1，2），则a的值为（）

A、0 B、1 C、2 D、3

查看试题解析
4. 在Rt△ABC中，∠ACB＝90°，AC＝6，AB＝10，以C为圆心，BC为半径作⊙C，则点A与⊙C的位置关系是（）

A、点A在⊙C内 B、点A在⊙C上 C、点A在⊙C外 D、无法确定

查看试题解析
5. 将抛物线y＝x²向右平移1个单位，再向上平移2个单位，所得的新抛物线的表达式为（）

A、y＝（x+1）²+2 B、y＝（x+2）²+1 C、y＝（x+2）²﹣1 D、y＝（x﹣1）²+2

查看试题解析
6. 已知点A（-1，a），B（2，b），C（4，c）均在抛物线y＝-（x-1）²-2上，则a，b，c的大小关系为（）

A、c＜a＜b B、b＜c＜a C、a＜c＜b D、b＜a＜c

查看试题解析
7. 如图，在△ABC中，∠ABC＝90°，AB＝4，BC＝3，D是AB的中点，DE⊥AC交AC于点E，则AE的长是（）

A、 $\frac{6}{5}$ B、 $\frac{8}{5}$ C、 $\frac{5}{3}$ D、1

查看试题解析
8. 筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧，如图1，点M表示筒车的一个盛水桶．如图2，当筒车工作时，盛水桶的运行路径是以轴心O为圆心.5米为半径的圆，旦圆心在水面上方，若圆被水面截得的弦AB长为8米，则筒车工作时，盛水桶在水面以下的最大深度为（）

A、1米 B、2米 C、3米 D、4米

查看试题解析
9. 如图，以正方形ABCD的点A为圆心，AB为半径作 $\overset{⌢}{B D}$ ，取 $\overset{⌢}{B D}$ 上一点F使得DF＝DC，点E是 $\overset{⌢}{B D}$ 上一点（不与点D，F重合），则∠DEF的值为（）

A、120° B、135° C、145° D、150°

查看试题解析
10. 如图，抛物线y＝ $\frac{1}{2}$ x²−2x+c与x轴交于点A，B两点，与y轴负半轴交于点C，其顶点为M，点D，E分别是AB，BM的中点，若△DEB与△ACD的面积比为9：10，则c的值为（）

A、- $\frac{3}{2}$ B、-2 C、- $\frac{5}{2}$ D、-3

查看试题解析

二、填空题（本题有6题，每小题5分，共30分）

11. 已知线段a＝4，b＝16，线段c是a，b的比例中项，那么c等于．

查看试题解析
12. 如图，在⊙O中，OA＝2，∠ACB＝30°，则弦AB的长度是．

查看试题解析
13. 二次函数y＝ax²+bx-3（a≠0）的图象经过点（1，-2），则代数式a+b的值为．

查看试题解析
14. 已知二次函数y＝ax²+bx+c（0≤x≤5）的图象如图所示，关于该函数在所给自变量取值范围内，y的取值范围为．

查看试题解析
15. 如图，在等腰△ABC中，BC＝AC，AB＝2，将△ABC绕着点A按顺时针方向旋转90°得到△AB'C'，连结B'C，若B'C∥AB，则五边形ABCB'C'的面积是．

查看试题解析
16. 如图，在Rt△ABC中，∠ACB＝90°，AC＜BC，CD平分∠ACB交AB于点D，以DB为直径作⊙O，分别交CD，BC于点E，F，连结BE，EF．则∠EBF＝度；若DE＝DC，BC＝8，则EF的长为．

查看试题解析

三、解答题（本题有8小题，共80分，）

17. 如图，已知△ABC∽△ADE，AB＝15，BD＝3，BC＝12，求DE的长．

查看试题解析
18. 如图，在6×6的正方形网格中，圆上A，B，C三点都在格点上，请按要求作出图中圆的圆心：①仅用无刻度直尺，且不能用直尺中的直角；②保留作图痕迹．

查看试题解析
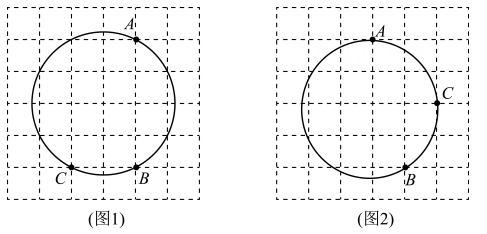19. 如图，在矩形ABCD中，AB＝2，BC＝4，E，F，G，H四点依次是边AB，BC，CD，DA上一点（不与各顶点重合），且AE＝AH＝CG＝CF，记四边形EFGH面积为S（图中阴影），AE＝x．

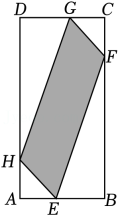(1)、求S关于x的函数表达式，并直接写出自变量的取值范围．

(2)、求x为何值时，S的值最大，并写出S的最大值．

查看试题解析
20. 如图所示，在矩形ABCD中，点E是边AD上一点，连结BE．过E作EF⊥BE交CD于F．

(1)、求证：△ABE∽△DEF．

(2)、若AB＝6，AE＝9，DE＝2，求EF的长．

查看试题解析
21. 已知二次函数y＝（x-1）（x-m）．

(1)、若二次函数的对称轴是直线x＝3，求m的值．

(2)、当m＞2，0≤x≤3时，二次函数的最大值是7，求函数表达式．

查看试题解析
22. 如图，E是半圆O上一点，C是 $\overset{⌢}{B E}$ 的中点，直径AB∥弦DC，交AE于点F．

(1)、求证：CF＝AF．

(2)、连结OE，当AB＝4，OE⊥CD时，求EF的值．

查看试题解析
23. 某商场销售成本为每件40元的商品．据市场调查分析，如果按每件50元销售，一周能卖出500件；若销售单价每涨1元，每周销量就减少10件．设销售单价为x（x≥50）元．

(1)、写出一周销售量y（件）与x（元）的函数关系式．

(2)、设一周销售获得毛利润w元，写出w与x的函数关系式，并确定当x在什么取值范围内变化时，毛利润w随x的增大而增大．

(3)、超市扣除销售额的20%作为该商品的经营费用，为使得一周内净利润（净利润＝毛利润-经营费用）最大，超市对该商品定价为元，最大净利润为元．

查看试题解析
24. 如图1，在平面直角坐标系中，点A（-4，0），点B是y轴正半轴上一点，以AB为直径作⊙M，A与C关于y轴对称，直线CM交⊙M于点D，E（点E在左侧），交y轴于点F．设OB＝a．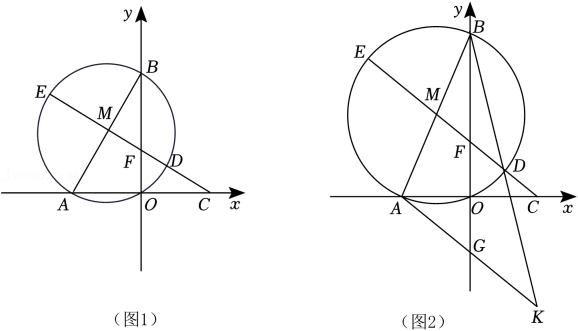

(1)、求M的坐标（用a的代数式表示）和AC的长．

(2)、若E是半圆AB的中点，求点E的坐标．

(3)、如图2，过点A作AG∥CE交y轴于点G，连结BD并延长交AG延长线于点K．
①试说明△ABK是等腰三角形．

②当点G为AK中点时，求a的值．

查看试题解析