2022-2023学年沪科版九年级上册 解直角三角形单元检测卷
试卷更新日期:2022-11-03 类型:单元试卷
一、单选题(每小题4分,共40分)
-
1. 如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为 ,则高BC是( )
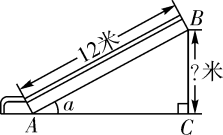 A、 米 B、 米 C、 米 D、 米2. 如图,河坝横断面迎水坡的坡比为: , 坝高m,则的长度为( )
A、 米 B、 米 C、 米 D、 米2. 如图,河坝横断面迎水坡的坡比为: , 坝高m,则的长度为( )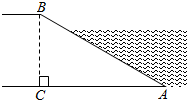 A、6m B、m C、9m D、m3. 在中, , 都是锐角,且 , , 则的形状是( )A、直角三角形 B、钝角三角形 C、等边三角形 D、不能确定4. 如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3000m的高空C处时,测得A处渔政船的俯角为45°,测得B处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB是( )
A、6m B、m C、9m D、m3. 在中, , 都是锐角,且 , , 则的形状是( )A、直角三角形 B、钝角三角形 C、等边三角形 D、不能确定4. 如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3000m的高空C处时,测得A处渔政船的俯角为45°,测得B处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB是( ) A、m B、m C、m D、m5. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )
A、m B、m C、m D、m5. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )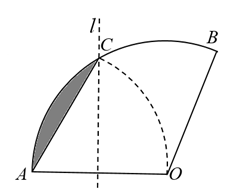 A、 B、 C、 D、6. 如图,的顶点均在正方形网格的格点上,则的值为( )
A、 B、 C、 D、6. 如图,的顶点均在正方形网格的格点上,则的值为( ) A、 B、2 C、 D、7. 如图,某建筑物的顶部有一块宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,米,米,则宣传牌CD的高度是( )米
A、 B、2 C、 D、7. 如图,某建筑物的顶部有一块宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,米,米,则宣传牌CD的高度是( )米 A、 B、 C、 D、8. 如图,在矩形中, , 点是上一点,将沿直线折叠,点落在矩形的内部点处,若 , 则的长为( )
A、 B、 C、 D、8. 如图,在矩形中, , 点是上一点,将沿直线折叠,点落在矩形的内部点处,若 , 则的长为( ) A、 B、 C、 D、9. 的值等于( )A、2 B、1 C、 D、10. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )
A、 B、 C、 D、9. 的值等于( )A、2 B、1 C、 D、10. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )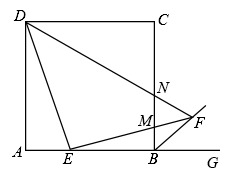 A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题(每空5分,共30分)
-
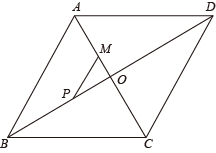
11. 在中, , , , 那么AB的长为 .12. 若等腰三角形一腰上的高与底边的夹角为 , 且高为 , 则这个等腰三角形的腰长为 , 面积为 .13. 如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且AM=3,点P为线段BD上的一个动点,则MP+PB的最小值是 .
 14. 小明用一块含有角()的直角三角尺测量校园内某棵树的高度,示意图如图所示.若小明的眼睛与地面之间的垂直高度为 , 小明与树之间的水平距离为 , 则这棵树的高度约为 . (结果精确到 , 参考数据:)
14. 小明用一块含有角()的直角三角尺测量校园内某棵树的高度,示意图如图所示.若小明的眼睛与地面之间的垂直高度为 , 小明与树之间的水平距离为 , 则这棵树的高度约为 . (结果精确到 , 参考数据:) 15. 如图,对折矩形纸片 , 使得与重合,得到折痕 , 把纸片展平,再一次折叠纸片,使点A的对应点落在上,并使折痕经过点B,得到折痕 . 连接 , 若 , , 则的长是 .
15. 如图,对折矩形纸片 , 使得与重合,得到折痕 , 把纸片展平,再一次折叠纸片,使点A的对应点落在上,并使折痕经过点B,得到折痕 . 连接 , 若 , , 则的长是 .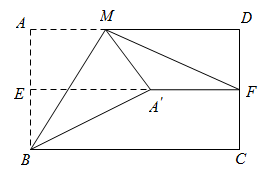
三、计算题(共10分)
-
16. 化简:(1)、(2)、 .
四、作图题(共13分)
-
17. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,线段的端点和点P均在格点上.请按要求完成作图,不写作法,保留作图痕迹.
 (1)、在图①中画一条以P为端点的射线 , 使其平分线段 , 点C在线段上;(2)、在图②中画一条以P为端点的射线 , 使其分线段为1:3两部分,点D在线段上;(3)、在图③中画一条以P为端点的射线 , 使 , 点E在线段上.
(1)、在图①中画一条以P为端点的射线 , 使其平分线段 , 点C在线段上;(2)、在图②中画一条以P为端点的射线 , 使其分线段为1:3两部分,点D在线段上;(3)、在图③中画一条以P为端点的射线 , 使 , 点E在线段上.五、解答题(共5题,共57分)
-
18. 如图,甲楼高 , 在甲楼楼顶处、楼底处分别测得乙楼楼顶处的仰角为 , . , 垂足为点 . 求乙楼的高度 .
 19. 如图,矩形中,是边上一动点,过点的反比例函数的图象与边相交于点 .
19. 如图,矩形中,是边上一动点,过点的反比例函数的图象与边相交于点 . (1)、点运动到边的中点时,求反比例函数的表达式;(2)、连接 , 求的值.20. 如图, 中, ,点 是边 的中点,以 为底边在其右侧作等腰三角形 ,使 ,连结 ,则:
(1)、点运动到边的中点时,求反比例函数的表达式;(2)、连接 , 求的值.20. 如图, 中, ,点 是边 的中点,以 为底边在其右侧作等腰三角形 ,使 ,连结 ,则: (1)、求证: ;(2)、若 ,求证: .
(1)、求证: ;(2)、若 ,求证: .
-
-

