山西省吕梁市柳林县2022—2023学年九年级上学期期中评估数学试题

试卷更新日期：2022-11-03 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程 $2 x^{2} - 6 x - 5 = 0$ 的一次项系数是（）

A、2 B、6 C、-6 D、-5

查看试题解析
2. 下列是部分星座的符号，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
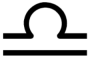3. 如图， $A B$ 是 $⊙ O$ 的直径，C为圆内一点，则下列说法正确的是（）

A、 $∠ B O C$ 是圆心角 B、 $A C$ 是 $⊙ O$ 的弦 C、 $∠ C$ 是圆周角 D、 $A C + O C < \frac{1}{2} A B$

查看试题解析
4. 某种商品每天的销售利润y（元）与单价x（元）之间的函数关系式为 $y = - 0.1 {(x - 3)}^{2} + 25$ ．则这种商品每天的最大利润为（）

A、0.1元 B、3元 C、25元 D、75元

查看试题解析
5. 在如图所示的方格纸（1格长为1个单位长度）中， $△ A B C$ 的顶点都在格点上，将 $△ A B C$ 绕点 $O$ 按顺时针方向旋转得到 $△ A^{'} B^{'} C^{'}$ ，使各顶点仍在格点上，则其旋转角的度数是（）

A、 $45 °$ B、 $60 °$ C、 $75 °$ D、 $90 °$

查看试题解析
6. 若将抛物线 $y = 2 x^{2} + 3$ 向右平移3个单位，再向上平移2个单位，则所得抛物线的解析式为（）

A、 $2 k + 9 k - 8 k = 15 ，$ B、 $y = 2 {(x - 3)}^{2} + 5$ C、 $y = 2 {(x + 3)}^{2} - 1$ D、 $y = 2 {(x - 3)}^{2} - 1$

查看试题解析
7. 某厂1月份生产口罩60万箱，第一季度生产口罩共200万箱，一位同学根据题意列出了方程 $60 + 60 (1 + x) + 60 {(1 + x)}^{2} = 200$ ，则x表示的意义是（）

A、该厂二月份的增长率 B、该厂三月份的增长率 C、该厂一、二月份平均每月的增长率 D、该厂二、三月份平均每月的增长率

查看试题解析
8. 如图，点P从右向左运动的运动路线在抛物线 $y = a {(x + 1)}^{2} - 1$ 上，点P第一次到达x轴时的坐标为 $A (1 ， 0)$ ，则当点P再次到达x轴时的坐标为（）

A、 $(- 2 ， 0)$ B、 $(- 2.5 ， 0)$ C、 $(- 3 ， 0)$ D、 $(- 3.5 ， 0)$

查看试题解析
9. 如图，点 $O$ 为线段 $B C$ 的中点，点 $A$ ， $C$ ， $D$ 到点 $O$ 的距离相等，则 $∠ A$ 与 $∠ C$ 的数量关系为（）

A、 $∠ A = ∠ C$ B、 $∠ A = 2 ∠ C$ C、 $∠ A - ∠ C = 90^{\circ}$ D、 $∠ A + ∠ C = 180^{\circ}$

查看试题解析
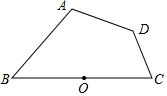10. 如图，抛物线 $y = a x^{2} + b x + c$ 与x轴相交于点 $A (- 2 ， 0)$ ， $B (6 ， 0)$ ，与y轴相交于点C，甲、乙、丙、丁四名同学在一起探究该函数的图象与性质，下面是他们得出的结论，其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 若二次函数 $y = (m - 1) x^{m^{2} + 1}$ 的图象开口向下，则m的值为．

查看试题解析
12. 在平面直角坐标系内，若点P（﹣1，p）和点Q（q，3）关于原点O对称，则pq的值为．

查看试题解析
13. 如图，点 $A ， B ， C$ 在 $⊙ O$ 上， $∠ A = 45 °$ ，则 $∠ B O C$ 的度数为．

查看试题解析
14. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ 、 $A B = 2 B C = 4$ ，将 $△ A B C$ 绕点A顺时针旋转 $60 °$ 得到 $△ A E D$ 、则 $C E$ 的长为．

查看试题解析
15. 如图，在平面直角坐标系中，点 $A (0 ， a^{2} - 2 a)$ 和点 $B (0 ， - 4 a - 5)$ 在y轴上，点M在x轴负半轴上， $S_{△ A B M} = 12$ ．当线段OM最长时，点M的坐标为．

查看试题解析

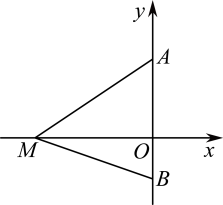
三、解答题

16.

(1)、解方程： $x^{2} - 4 x = 0$ ．

(2)、如图，已知 $∠ B A C = 30 °$ ，把 $△ A B C$ 绕着点A顺时针旋转，使得点B与 $C A$ 的延长线上的点D重合．求 $∠ A E C$ 的度数．

查看试题解析
17. 疫情期间“停课不停学”，因此王老师在线上开通公众号进行公益授课，4月份该公众号关注人数为6000，6月份该公众号关注人数达到7260，若从4月份到6月份，每月该公众号关注人数的平均增长率都相同，求该公众号关注人数的月平均增长率．

查看试题解析
18. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = x^{2} + x - 2$ 与x轴交于点A，B，与y轴交于点C．

(1)、求顶点D的坐标．

(2)、求 $△ A B C$ 的面积．

查看试题解析
19. 关于x的一元二次方程mx²﹣（2m﹣3）x+（m﹣1）=0有两个实数根．

(1)、求m的取值范围；

(2)、若m为正整数，求此方程的根．

查看试题解析
20. 已知：如图，将 $△ A B C$ 绕点 $C$ 旋转一定角度得到 $△ E D C$ ，若 $∠ A C E = 2 ∠ A C B$ ．

(1)、求证： $△ A D C ≅ △ A B C$ ；

(2)、若 $A B = B C = 5$ ， $A C = 6$ ，求四边形 $A B C D$ 的面积．

查看试题解析
21. 如图， $A B$ 是半 $⊙ O$ 的直径， $C ， D$ 是圆上两点，且 $O D ∥ A C$ ， OD与BC交于点E．

(1)、求证：E为 $B C$ 的中点．

(2)、若 $B C = 6$ ， $D E = 2$ ，求 $A B$ 的长度．

查看试题解析
22. 已知抛物线 $y = x^{2} + (2 m + 2) x + m^{2} + m - 1$ （m是常数）．

(1)、用含m的代数式表示该二次函数图象的顶点坐标．

(2)、当二次函数图象的顶点在x轴上时，求m的值及此时顶点的坐标．

(3)、小明研究发现：无论m取何值，抛物线的顶点都在同一条直线上．请写出这条直线的解析式，并加以证明．

查看试题解析
23. 综合与实践
已知 $△ A B C$ 与 $△ B D E$ 均为等腰直角三角形，其中 $∠ B A C = ∠ B D E = 90 °$ ，连接 $C E$ ， P是 $E C$ 的中点，连接 $P A ， P D$ ．

(1)、【初步感知】
如图1，当 $B ， D ， C$ 三点在同一直线上时， $P A$ 和 $P D$ 的数量关系为，位置关系为．

(2)、【深入探究】
如图2，当 $B ， D ， A$ 三点在同一直线上时，（1）中得到的结论成立吗？请加以证明．

(3)、【拓展提高】
如图3，若等腰直角 $△ A B C$ 绕点B逆时针旋转，当 $E C$ 恰好与 $B D$ 平行时，（1）中得到的结论还成立吗？请加以证明．

查看试题解析