北京市海淀区2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-11-03 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程 $3 x^{2} - 6 x - 4 = 0$ 的二次项系数、一次项系数、常数项分别是（）

A、3，6，4 B、3，-6，4 C、3，6，-4 D、3，-6，-4

查看试题解析
2. 将抛物线 $y = - x^{2} + 1$ 向上平移2个单位长度，得到的抛物线是（）

A、 $y = - x^{2} + 3$ B、 $y = - (x - 2)^{2} + 1$ C、 $y = - x^{2} - 1$ D、 $y = - (x + 2)^{2} + 1$

查看试题解析
3. 下列四幅图案中，可以由右侧的一笔画“天鹅”旋转 $180 °$ 得到的图案是（）

A、 B、 C、 D、

查看试题解析
4. 如图， $B D$ 是 $△ A B C$ 的中线， $E$ ， $F$ 分别是 $B D$ ， $B C$ 的中点，连接EF．若 $A D = 4$ ，则 $E F$ 的长为（）

A、 $\frac{3}{2}$ B、2 C、 $\frac{5}{2}$ D、4

查看试题解析
5. 用配方法解方程 $x^{2} - 4 x + 1 = 0$ 时，结果正确的是（）

A、 ${(x - 2)}^{2} = 5$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x + 2)}^{2} = 5$ D、 ${(x + 2)}^{2} = 3$

查看试题解析
6. 二次函数 $y = a x^{2} + b x + c$ 的x与y的部分对应值如下表：
$x$
-1
0
1
2
3
4
$y$
$m$
2
1
2
5
10
则 $m$ 的值是（）

A、1 B、2 C、5 D、10

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ B A C = 135 °$ ，将 $△ A B C$ 绕点 $C$ 逆时针旋转得到 $△ D E C$ ，点 $A ， B$ 的对应点分别为 $D ， E$ ，连接 $A D$ ．当点 $A ， D ， E$ 在同一条直线上时，下列结论错误的是（）

A、 $△ A B C ≌ △ D E C$ B、 $∠ A D C = 45 °$ C、 $A D = \sqrt{2} A C$ D、 $A E = A B + C D$

查看试题解析
8. 如图，已知关于x的一元二次方程 $a (x - k)^{2} - 1 = 0$ 的两根在数轴上对应的点分别在区域①和区域②，区域均含端点，则k的值可能是（）

A、-1 B、0 C、1 D、2

查看试题解析

二、填空题

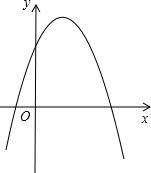
9. 若1是关于x的方程 $x^{2} - a x = 0$ 的根，则a的值为．

查看试题解析
10. 已知 $▱ A B C D$ 的周长为 $14 ， A B = 3$ ，则 $B C$ 的长为．

查看试题解析
11. 若二次函数y＝ax²+bx+c的图象如图所示，则ac0（填“＞”或“＝”或“＜”）．

查看试题解析
12. 如图，等边 $△ A B C$ 绕顶点 $A$ 逆时针旋转 $80 °$ 得到 $△ A D E$ ，连接 $B E$ ，则 $∠ A B E =$ $°$ ．

查看试题解析
13. 若关于x的一元二次方程 $x^{2} + x + k = 0$ 有两个相等的实数根，则k的值为．

查看试题解析
14. 如图是某停车场的平面示意图，停车场外围的长为30米，宽为18米．停车场内车道的宽都相等．停车位总占地面积为288平方米．设车道的宽为x米，可列方程为．

查看试题解析
15. 点 $A (2 ， y_{1}) ， B (a ， y_{2})$ 在二次函数 $y = x^{2} - 2 x + 3$ 的图象上．若 $y_{1} < y_{2}$ ，写出一个符合条件的a的值．

查看试题解析
16. 甲、乙、丙三名同学每人抽取一张卡片，每张卡片上有一个形如 $y = a x^{2} + b x $ 的二次函数的解析式，其中只有一人与其他两人抽到的解析式不同．下面是他们对抽到的解析式所对应的图象的描述：
甲：开口向下；
乙：顶点在第三象限；
丙：经过点（-2，0），（1，3）．
根据描述可知，抽到与其他两人解析式不同的是（填“甲”，“乙”或“丙”）．

查看试题解析

三、解答题

17. 解方程：

(1)、 $4 x^{2} = 9$ ；

(2)、 $x^{2} - 6 x + 8 = 0$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，将 $△ A B C$ 绕点C顺时针旋转 $90 °$ 得到 $△ D E C$ ，点A与点D对应，点B与点E对应．

(1)、依题意补全图形；

(2)、直线AB与直线DE的位置关系为．

查看试题解析
19. 已知 $m$ 是方程 $x^{2} + 2 x - 4 = 0$ 的一个根，求代数式 $(m + 2)^{2} + (m + 3) (m - 3)$ 的值．

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ C = 90 ° ， ∠ B = 20 °$ ，将 $△ A B C$ 绕点A顺时针旋转 $25 °$ 得到 $△ A D E$ ， $A D$ 交 $B C$ 于点F．若 $A E = 3$ ，求 $A F$ 的长．

查看试题解析
21. 在平面直角坐标系 $x O y$ 中，抛物线 $y = x^{2} + b x + c$ 经过 $A (0 ， 3)$ 和 $B (1 ， 0)$ 两点．

(1)、求该抛物线的解析式；

(2)、该抛物线的对称轴为．

查看试题解析
22. 已知关于x的一元二次方程 $x^{2} ＋（ m - 6 ） x - 6 m = 0$ ．

(1)、求证：该方程总有两个实数根；

(2)、若该方程有一个实数根小于2，求m的取值范围．

查看试题解析
23. 在平面直角坐标系xOy中，二次函数 $y = {(x - 1)}^{2} - 1$ 图象顶点为A，与x轴正半轴交于点B．

(1)、求点B的坐标，并画出这个二次函数的图象；

(2)、一次函数 $y = k x + b$ 的图象过A，B两点，结合图象，直接写出关于x的不等式 $k x + b > {(x - 1)}^{2} - 1$ 的解集．

查看试题解析
24. 如图，在△ABC中， $∠ A B C = 90 °$ ， BD为△ $A B C$ 的中线． $B E ∥ D C$ ， $B E = D C$ ，连接CE．

(1)、求证：四边形BDCE为菱形；

(2)、连接DE，若 $∠ A C B = 60 °$ ， $B C = 4$ ，求DE的长．

查看试题解析
25. 探照灯的内部可以看成是抛物线的一部分经过旋转得到的抛物曲面．其原理是过某一特殊点的光线，经抛物线反射后所得的光线平行于抛物线的对称轴，我们称这个特殊点为抛物线的焦点．若抛物线的表达式为 $y = a x^{2}$ ，则抛物线的焦点为 $(0 ，$ $\frac{1}{4 a}$ $)$ ．如图，在平面直角坐标系 $x O y$ 中，某款探照灯抛物线的表达式为 $y = \frac{1}{4} x^{2}$ ，焦点为F．

(1)、点F的坐标是；

(2)、过点F的直线与抛物线交于A，B两点，已知沿射线FA方向射出的光线，反射后沿射线 $A M$ 射出， $A M$ 所在直线与x轴的交点坐标为 $(4 ， 0)$ ．
① 画出沿射线 $F B$ 方向射出的光线的反射光线 $B P$ ；
② $B P$ 所在直线与x轴的交点坐标为 ▲ ．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，已知抛物线 $y = x^{2} - 2 m x + m^{2} - 2$ ．

(1)、求抛物线的顶点坐标（用含 $m$ 的式子表示）；

(2)、已知点 $P (3 ， 2)$ ．
① 当抛物线过点 $P$ 时，求 $m$ 的值；
② 点 $Q$ 的坐标为 $(m ， 1)$ ．若抛物线与线段 $P Q$ 恰有一个公共点，结合函数图象，直接写出 $m$ 的取值范围．

查看试题解析
27. 在等边△ABC中，将线段CA绕点C逆时针旋转α（0°<α<30°）得到线段CD，线段CD与线段AB交于点E，射线AD与射线CB交于点F．

(1)、① 依题意补全图形；
② 分别求∠CEB和∠AFC的大小（用含α的式子表示）；

(2)、用等式表示线段BE，CE，CF之间的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系xOy中，已知点 $A (a ， b)$ ．对于点 $P (x ， y)$ 给出如下定义：当 $x \neq a$ 时，若实数k满足 $| y - b | = k | x - a |$ ，则称k为点P关于点A的距离系数．若图形M上所有点关于点A的距离系数存在最小值，则称此最小值为图形M关于点A的距离系数．

(1)、当点A与点O重合时，在 $P_{1} (2 ， 2) ， P_{2} (- 2 ， 1) ， P_{3} (- 4 ， 4)$ 中，关于点A的距离系数为1的是；

(2)、已知点 $B (- 2 ， 1) ， C (1 ， 1)$ ，若线段BC关于点 $A (m ， - 1)$ 的距离系数小于 $\frac{1}{2}$ ，则m的取值范围为；

(3)、已知点 $A (4 ， 0) ， T (0 ， t)$ ，其中 $2 \leq t \leq 4$ ．以点T为对角线的交点作边长为2的正方形，正方形的各边均与某条坐标轴垂直，点D，E为该正方形上的动点，线段 $D E$ 的长度是一个定值（ $0 < D E < 2$ ）．
① 线段 $D E$ 关于点A的距离系数的最小值为；

② 若线段 $D E$ 关于点A的距离系数的最大值是 $\frac{3}{2}$ ，则 $D E$ 的长为．

查看试题解析

$x$	-1	0	1	2	3	4
$y$	$m$	2	1	2	5	10