2023中考数学真题复习第01讲 规律探索类
试卷更新日期:2022-11-03 类型:一轮复习
一、单选题(每题2分,共18分)
-
1. 按一定规律排列的一组数据: , , , , , , ….则按此规律排列的第10个数是( )A、 B、 C、 D、2. 生物学中,描述、解释和预测种群数量的变化,常常需要建立数学模型.在营养和生存空间没有限制的情况下,某种细胞可通过分裂来繁殖后代,我们就用数学模型2n来表示.即:21=2,22=4,23=8,24=16,25=32,……,请你推算22022的个位数字是( )A、8 B、6 C、4 D、23. 把菱形按照如图所示的规律拼图案,其中第①个图案中有 1个菱形,第②个图案中有 3个菱形,第③个图案中有5个菱形,…,按此规律排列下去,则第⑥个图案中菱形的个数为( )
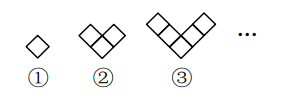 A、15 B、13 C、11 D、94. 用正方形按如图所示的规律拼图案,其中第①企图案中有5个正方形,第②个图案中有9个正方形,第③全图案中有13全正方形,第④个图案中有17企正方形,此规律排列下去,则第⑨个图案中正方形的个数为( )
A、15 B、13 C、11 D、94. 用正方形按如图所示的规律拼图案,其中第①企图案中有5个正方形,第②个图案中有9个正方形,第③全图案中有13全正方形,第④个图案中有17企正方形,此规律排列下去,则第⑨个图案中正方形的个数为( ) A、32 B、34 C、37 D、415. 将全体正偶数排成一个三角形数阵:
A、32 B、34 C、37 D、415. 将全体正偶数排成一个三角形数阵:
按照以上排列的规律,第10行第5个数是( )
A、98 B、100 C、102 D、1046. 如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点……按照此规律,第一百幅图中圆点的个数是( )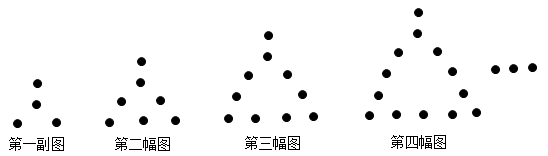 A、297 B、301 C、303 D、4007. 如图,用若干根相同的小木棒拼成图形,拼第1个图形需要6根小木棒,拼第2个图形需要14根小木棒,拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒,则n的值为( )
A、297 B、301 C、303 D、4007. 如图,用若干根相同的小木棒拼成图形,拼第1个图形需要6根小木棒,拼第2个图形需要14根小木棒,拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒,则n的值为( ) A、252 B、253 C、336 D、3378. 由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为( )
A、252 B、253 C、336 D、3378. 由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为( )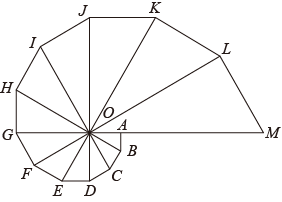 A、()3 B、()7 C、()6 D、()69. 如图,在平面直角坐标系中,将边长为2的正六边形绕点顺时针旋转个 , 得到正六边形 , 当时,正六边形的顶点的坐标是( )
A、()3 B、()7 C、()6 D、()69. 如图,在平面直角坐标系中,将边长为2的正六边形绕点顺时针旋转个 , 得到正六边形 , 当时,正六边形的顶点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空1分,共4分)
-
10. 按一定规律排列的数据依次为 , , , ……按此规律排列,则第30个数是 .11. 木材加工厂将一批木料按如图所示的规律依次摆放,则第个图中共有木料根.
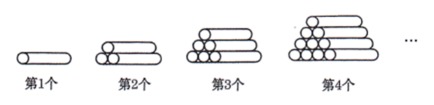 12. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .
12. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .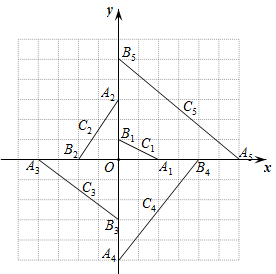 13. 如图,是等边三角形,直线经过它们的顶点 , 点在x轴上,则点的横坐标是.
13. 如图,是等边三角形,直线经过它们的顶点 , 点在x轴上,则点的横坐标是.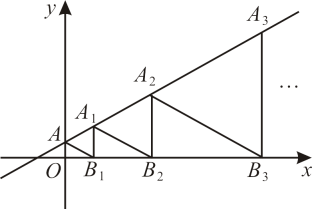
三、综合题(共13题,共78分)
-
14. 观察下列图形规律,当图形中的“○”的个数和“.”个数差为2022时,n的值为 .
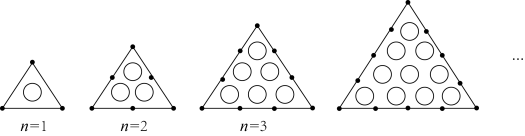 15. 古希腊的毕达哥拉斯学派对整数进行了深入的研究,尤其注意形与数的关系,“多边形数”也称为“形数”,就是形与数的结合物.用点排成的图形如下:其中:图①的点数叫做三角形数,从上至下第一个三角形数是1,第二个三角形数是 ,第三个三角形数是 ,……图②的点数叫做正方形数,从上至下第一个正方形数是1,第二个正方形数是 ,第三个正方形数是 ,……由此类推,图④中第五个正六边形数是.
15. 古希腊的毕达哥拉斯学派对整数进行了深入的研究,尤其注意形与数的关系,“多边形数”也称为“形数”,就是形与数的结合物.用点排成的图形如下:其中:图①的点数叫做三角形数,从上至下第一个三角形数是1,第二个三角形数是 ,第三个三角形数是 ,……图②的点数叫做正方形数,从上至下第一个正方形数是1,第二个正方形数是 ,第三个正方形数是 ,……由此类推,图④中第五个正六边形数是.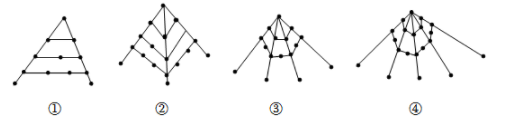 16. 如图,将正整数按此规律排列成数表,则2021是表中第行第列.
16. 如图,将正整数按此规律排列成数表,则2021是表中第行第列. 17. 古希腊数学家把1,3,6,10,15,21,…这样的数叫做三角形数,因为它的规律性可以用如图表示.根据图形,若把第一个图形表示的三角形数记为 ,第二个图形表示的三角形数记为 ,…,则第 个图形表示的三角形数 =.(用含 的式子表达)
17. 古希腊数学家把1,3,6,10,15,21,…这样的数叫做三角形数,因为它的规律性可以用如图表示.根据图形,若把第一个图形表示的三角形数记为 ,第二个图形表示的三角形数记为 ,…,则第 个图形表示的三角形数 =.(用含 的式子表达) 18. 在2020年新冠肺炎疫情期间,某中学响应政府有“停课不停学”的号召,充分利用网络资源进行网上学习,九年级1班的全体同学在自主完成学习任务的同时,彼此关怀,全班每两个同学都通过一次电话,互相勉励,共同提高,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全同学共通过多少次电话呢?我们可以用下面的方式来解决问题.
18. 在2020年新冠肺炎疫情期间,某中学响应政府有“停课不停学”的号召,充分利用网络资源进行网上学习,九年级1班的全体同学在自主完成学习任务的同时,彼此关怀,全班每两个同学都通过一次电话,互相勉励,共同提高,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全同学共通过多少次电话呢?我们可以用下面的方式来解决问题.用点A1、A2、A3…A48分表示第1名同学、第2名同学、第3名同学…第48名同学,把该班级人数x与通电话次数y之间的关系用如图模型表示:
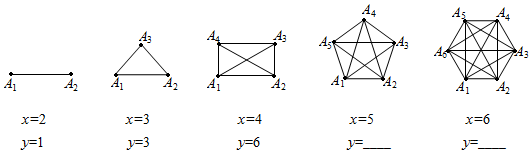 (1)、填写上图中第四个图中y的值为 , 第五个图中y的值为.(2)、通过探索发现,通电话次数y与该班级人数x之间的关系式为 , 当x=48时,对应的y=.(3)、若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?19.
(1)、填写上图中第四个图中y的值为 , 第五个图中y的值为.(2)、通过探索发现,通电话次数y与该班级人数x之间的关系式为 , 当x=48时,对应的y=.(3)、若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?19.用同样大小的黑色棋子按如图所示的规律摆放:
 (1)、第5个图形有多少黑色棋子?(2)、第几个图形有2013颗黑色棋子?请说明理由.20. “分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
(1)、第5个图形有多少黑色棋子?(2)、第几个图形有2013颗黑色棋子?请说明理由.20. “分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.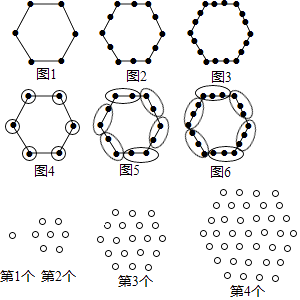
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
(1)、我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是、 .
(2)、请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:①第5个点阵中有个圆圈;第n个点阵中有个圆圈.
②小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
21. 设 是一个两位数,其中a是十位上的数字(1≤a≤9).例如,当a=4时, 表示的两位数是45.(1)、尝试:①当a=1时,152=225=1×2×100+25;
②当a=2时,252=625=2×3×100+25;
③当a=3时,352=1225=;
……
(2)、归纳: 与100a(a+1)+25有怎样的大小关系?试说明理由.(3)、运用:若 与100a的差为2525,求a的值.22. 观察以下等式:第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: ,
……
按照以上规律.解决下列问题:
(1)、写出第5个等式:;(2)、写出你猜想的第n个等式(用含n的式子表示),并证明.23. 观察下面的等式: , , ,……(1)、按上面的规律归纳出一个一般的结论(用含n的等式表示,n为正整数).(2)、请运用分式的有关知识,推理说明这个结论是正确的。24. 观察以下等式:第1个等式:
第 个等式:
第3个等式:
第 个等式:
第5个等式:
······
按照以上规律.解决下列问题:
(1)、写出第6个等式;(2)、写出你猜想的第n个等式:(用含n的等式表示),并证明.