人教版数学七年级下课时精炼5.3.1平行线的性质
试卷更新日期:2022-11-02 类型:同步测试
一、单选题
-
1. 如图,将一副三角板的直角顶点重合,且使 , 则的度数是( )
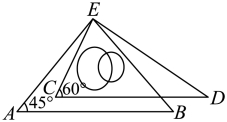 A、 B、 C、 D、2. 如图所示, , , 若 , 则的度数为( )
A、 B、 C、 D、2. 如图所示, , , 若 , 则的度数为( ) A、100° B、110° C、120° D、130°
A、100° B、110° C、120° D、130°二、填空题
-
3. 如图, , 与互补,当 , 时,的度数为 .
 4. 如图 , AB与CE的关系是 , 此时若∠3=30°,则∠B=°.
4. 如图 , AB与CE的关系是 , 此时若∠3=30°,则∠B=°.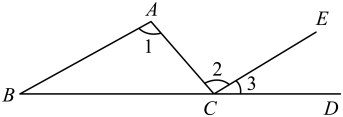 5. 如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是 .
5. 如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是 .
三、解答题
-
6. 如图,已知 , . 求证: .
 7. 如图, , . 求证: .
7. 如图, , . 求证: .
证明:∵( ),( ),
∴( ),∴( ),
∴( ),
∵( ),
∴( ),
∴( ).
8. 如图,点P为∠AOB的角平分线OC上的一点,过点P作PM∥OB交OA于点M,过点P作PN⊥OB于点N.当∠AOB=60°时,求∠OPN的度数.
解:∵PN⊥OB于点N,
∴∠PNB= ▲ °( )(填推理的依据).
∵PM∥OB,
∴∠MPN=∠PNB=90°,
∠POB= ▲ ( )(填推理的依据).
∵OP平分∠AOB,且∠AOB=60°,
∴∠POB=∠AOB=30°(角的平分线的定义).
∴∠MPO= ▲ °.
∵∠MPO+∠OPN=∠MPN,
∴∠OPN= ▲ °.
9. 请把下列说理过程补充完整,并在括号内填上相应的根据.如图,已知 , ,
请对说明理由.

理由:∵(已知)
( )
∴( )
∴ ▲ ▲ ( ).
∴( ).
∵(已知)
∴( )
∴( )
∴(等量代换)
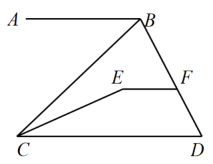
10. 如图所示,在△ABC中,E,G分别是BC,AC上的点,D,F是AB上的点,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2, 试判断∠AGD和∠ACB是否相等,为什么? 11. 完成下列证明过程,并在括号内填上依据.
11. 完成下列证明过程,并在括号内填上依据.如图,点E在上,点在上, , . 求证:ABCD.

证明:(已知),(),
▲ (等量代换),
▲ 同位角相等,两直线平行 ,
C( ).
又(已知),
( ),
( ) .
12. 请将下列证明过程补充完整:已知:如图,点P在CD上,已知 , .

求证:
证明:∵(已知)
∴▲ // ▲ ( )
∴ ▲ ( )
又∵(已知)
∴ ▲
即 ▲ (等式的性质)
∴//(内错角相等,两直线平行)
∴( )
四、综合题
-
13. 如图①,已知AD∥BC,∠B=∠D=120°.

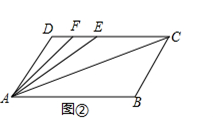 (1)、请问:AB与CD平行吗?为什么?(2)、若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.(3)、若点E在直线CD上,且满足∠EAC=∠BAC,求∠ACD:∠AED的值(请自己画出符合题意图形,并解答).14. 如图1,已知AB//CD,点G在上,点H在上,连接、 , , .
(1)、请问:AB与CD平行吗?为什么?(2)、若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.(3)、若点E在直线CD上,且满足∠EAC=∠BAC,求∠ACD:∠AED的值(请自己画出符合题意图形,并解答).14. 如图1,已知AB//CD,点G在上,点H在上,连接、 , , . (1)、求证:AB//EF;(2)、如图2,若 , 延长交的延长线于点M,请直接写出图2中所有与互余的角.15. 如图:
(1)、求证:AB//EF;(2)、如图2,若 , 延长交的延长线于点M,请直接写出图2中所有与互余的角.15. 如图: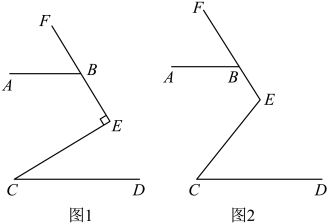 (1)、如图1,∠CEF=90°,点B在射线EF上,若∠ABF=50°,∠C=40° ,试判断AB、CD的位置关系,并说明理由;(2)、如图2,∠CEF=120° ,点B在射线EF上,且 . 则∠ABE与∠C的数量关系为:16. 如图,已知AB∥CD.直线EF分别交直线AB、CD于点E、F,∠EFB=∠B,FH⊥FB.
(1)、如图1,∠CEF=90°,点B在射线EF上,若∠ABF=50°,∠C=40° ,试判断AB、CD的位置关系,并说明理由;(2)、如图2,∠CEF=120° ,点B在射线EF上,且 . 则∠ABE与∠C的数量关系为:16. 如图,已知AB∥CD.直线EF分别交直线AB、CD于点E、F,∠EFB=∠B,FH⊥FB. (1)、求证:FH平分∠GFD.(2)、若∠B=20°,求∠DFH的度数;17. 如图, , .
(1)、求证:FH平分∠GFD.(2)、若∠B=20°,求∠DFH的度数;17. 如图, , . (1)、请按要求填空并说明;
(1)、请按要求填空并说明;解:因为 ,
所以 , (根据: )
又因为 ,
所以▲ ,
所以 ,
∴(根据: );
(2)、若平分 , 于点 , , 请直接写出的度数.18. 如图, , , , , 点P是上的一点. (1)、求的度数;(2)、若 , 请判断与是否平行.19. 如图,平分交于点 , 点在的延长线上,点在线段上,与相交于点 , .
(1)、求的度数;(2)、若 , 请判断与是否平行.19. 如图,平分交于点 , 点在的延长线上,点在线段上,与相交于点 , . (1)、 与平行吗?请说明理由;(2)、若点在的延长线上,且 , , 求的度数.20. 在一次数学综合实践活动课上,同学们进行了如下探究活动:将一块等腰直角三角板的顶点G放置在直线上,旋转三角板.
(1)、 与平行吗?请说明理由;(2)、若点在的延长线上,且 , , 求的度数.20. 在一次数学综合实践活动课上,同学们进行了如下探究活动:将一块等腰直角三角板的顶点G放置在直线上,旋转三角板.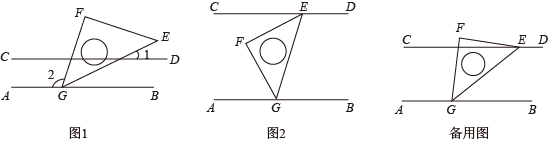 (1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.21. 问题:已知线段AB∥CD,在AB、CD间取一点P(点P不在直线AC上),连接PA、PC,试探索∠APC与∠A、∠C之间的关系.
(1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.21. 问题:已知线段AB∥CD,在AB、CD间取一点P(点P不在直线AC上),连接PA、PC,试探索∠APC与∠A、∠C之间的关系. (1)、端点A、C同向:
(1)、端点A、C同向:如图1,点P在直线AC右侧时,∠APC﹣(∠A+∠C)=度;
如图2,点P在直线AC左侧时,∠APC+(∠A+∠C)=度;
(2)、端点A、C反向:如图3,点P在直线AC右侧时,∠APC与∠A﹣∠C有怎样的等量关系?写出结论并证明;
如图4,点P在直线AC左侧时,∠APC﹣(∠A﹣∠C)= ▲ 度.
22. 已知:如图,直线 , 点C是PQ,MN之间(不在直线PQ,MN上)的一个动点.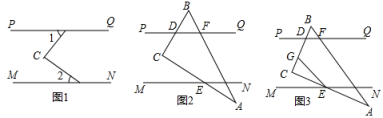 (1)、若∠1与∠2都是锐角,如图1,请直接写出∠C与∠1∠2之间的数量关系.(2)、若小明把一块三角板(∠A=30°,∠C=90°)如图2放置,点D,E,F是三角板的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数.(3)、将图2中的三角板进行适当转动,如图3,直角顶点C始终在两条平行线之间,点G在线段CD上,连结EG,且有∠CEG=∠CEM,给出下列两个结论:
(1)、若∠1与∠2都是锐角,如图1,请直接写出∠C与∠1∠2之间的数量关系.(2)、若小明把一块三角板(∠A=30°,∠C=90°)如图2放置,点D,E,F是三角板的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数.(3)、将图2中的三角板进行适当转动,如图3,直角顶点C始终在两条平行线之间,点G在线段CD上,连结EG,且有∠CEG=∠CEM,给出下列两个结论:①的值不变;
②∠GEN-∠BDF的值不变.
其中只有一个是正确的,你认为哪个是正确的?讲求出不变的值是多少.
23. 如图1,点E、F分别在直线AB、CD上,点P为AB、CD之间的一点,且 .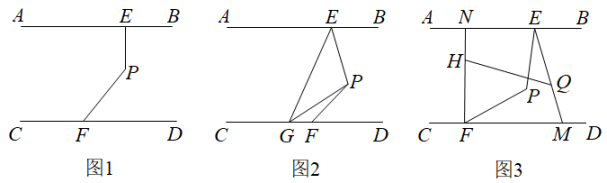 (1)、求证:;(2)、如图2,点G在射线FC上,PG平分 , , 探究与之间的数量关系.并说明理由;(3)、如图3, , . 直线HQ分别交FN,EM于H、Q两点,若 , 求的度数.24. 如图①, , 点A,C分别在射线FE和FH上, .
(1)、求证:;(2)、如图2,点G在射线FC上,PG平分 , , 探究与之间的数量关系.并说明理由;(3)、如图3, , . 直线HQ分别交FN,EM于H、Q两点,若 , 求的度数.24. 如图①, , 点A,C分别在射线FE和FH上, .
 (1)、若 , 则的度数为;(2)、小明同学发现,无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法:如图②,过点A作 , 交CD于点M.请你根据小明同学提供的辅助线,确定该定值,并说明理由;(3)、如图③,把“”改为“”,其他条件保持不变,猜想与的数量关系,并说明理由.
(1)、若 , 则的度数为;(2)、小明同学发现,无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法:如图②,过点A作 , 交CD于点M.请你根据小明同学提供的辅助线,确定该定值,并说明理由;(3)、如图③,把“”改为“”,其他条件保持不变,猜想与的数量关系,并说明理由.