人教版数学七年级下课时精炼5.2.2平行线的判定
试卷更新日期:2022-11-02 类型:同步测试
一、单选题
-
1. 如图,点E在BC的延长线上,下列条件中能判定CDAB的是()
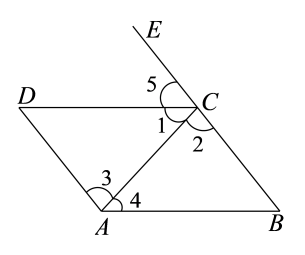
①∠1=∠4②∠2=∠3③∠5=∠B④∠DCB+∠B=180°
A、①②③④ B、①②③ C、①③④ D、①②2. 如图,点在的延长线上,对于给出的四个条件: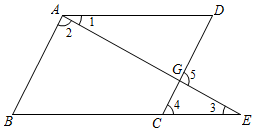
①;②;③;④ , 其中能判断的是( )
A、①② B、②③ C、③④ D、①④3. 如图所示,AE平分∠BAC,CE平分∠ACD,则不能判定AB∥CD的条件是( ) A、∠1=∠2 B、∠1+∠2=90° C、∠3+∠4=90° D、∠2+∠3= 90°4. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度和方向可能是( )A、第一次向右拐40°,第二次向左拐140° B、第一次向左拐40°.第二次向右拐40° C、第一次向左拐40°,第二次向左拐140° D、第一次向右拐40°,第二次向右拐40°5. 在下列选项图中,若∠1=∠2,则能判断AB∥CD的是( )A、
A、∠1=∠2 B、∠1+∠2=90° C、∠3+∠4=90° D、∠2+∠3= 90°4. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度和方向可能是( )A、第一次向右拐40°,第二次向左拐140° B、第一次向左拐40°.第二次向右拐40° C、第一次向左拐40°,第二次向左拐140° D、第一次向右拐40°,第二次向右拐40°5. 在下列选项图中,若∠1=∠2,则能判断AB∥CD的是( )A、 B、
B、 C、
C、 D、
D、 6. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )
6. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )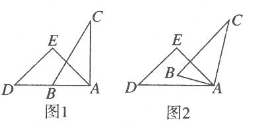 A、 和 B、 和 C、 和 D、以上都有可能
A、 和 B、 和 C、 和 D、以上都有可能二、填空题
-
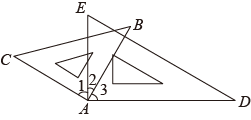
7. 如图,将一副三角板按如图放置,则下列结论:①;②当时,则有;③当时,则有;④当时,则有 . 其中正确的序号是 .
三、解答题
-
8. 如图,分别平分和 , 且 , 求证: .
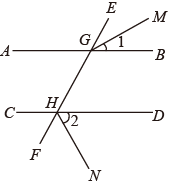 9. 已知: , 点G在上,B、C、G三点在同一条直线上,且 , , 求证: .
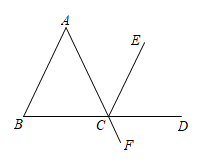
9. 已知: , 点G在上,B、C、G三点在同一条直线上,且 , , 求证: . 10. 如图AF 与BD相交于点C,∠B=∠ACB, 且CD平分∠ECF.求证: .
10. 如图AF 与BD相交于点C,∠B=∠ACB, 且CD平分∠ECF.求证: .请完成下列推理过程:
证明:∵CD 平分∠ECF
∴∠ECD= ▲ ( )
∵∠ACB=∠FCD( )
∴∠ECD=∠ACB( )
∵∠B=∠ACB
∴∠B=∠▲( )
∴ ( ).
11. 已知:如图,CF平分∠ACM,∠1=72°,∠2=36°,判断CM与DN是否平行,并说明理由. 12. 完成下面的证明:如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,求证:AB∥CD.
12. 完成下面的证明:如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,求证:AB∥CD.
完成推理过程:
BE平分∠ABD(已知),
∴∠ABD=2∠α( ).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β( )
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( )
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°( ).
∴AB∥CD( ).
13. 如图, , , .问吗?为什么? 14. 如图,点E,F在分别在直线AB,CD上,∠AEF=70°,EM平分∠AEF交CD于点P,点N在直线CD上,且PN=PM,连接MN,若∠PMN=72.5°,判断直线AB与CD是否平行?并说明理由.
14. 如图,点E,F在分别在直线AB,CD上,∠AEF=70°,EM平分∠AEF交CD于点P,点N在直线CD上,且PN=PM,连接MN,若∠PMN=72.5°,判断直线AB与CD是否平行?并说明理由.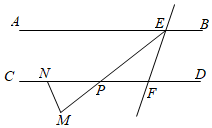 15. 已知:如图, , , 与 互补,求证:
15. 已知:如图, , , 与 互补,求证:
四、综合题
-
16. 如图,B,F,E,C在同一条直线上,∠A=∠D.
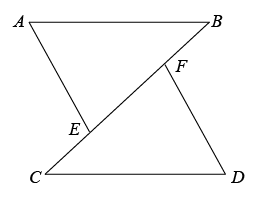 (1)、若∠A=78°,∠C=47°,求∠BFD的度数.(2)、若∠AEB+∠BFD=180°,求证:AB∥CD.17. 如图1,BD是△ABC的角平分线,作∠BDE = ∠ABD交AB于点E.
(1)、若∠A=78°,∠C=47°,求∠BFD的度数.(2)、若∠AEB+∠BFD=180°,求证:AB∥CD.17. 如图1,BD是△ABC的角平分线,作∠BDE = ∠ABD交AB于点E.
 (1)、求证:ED∥BC;(2)、若AC⊥BD,点M为线段AC延长线上一点(不与点c重合),连接BM,若AB⊥BM,在图2中补全图形并证明:∠DBC = ∠BMA.18. 如图,在中, , 垂足为D,点E在上, , 垂足为F.
(1)、求证:ED∥BC;(2)、若AC⊥BD,点M为线段AC延长线上一点(不与点c重合),连接BM,若AB⊥BM,在图2中补全图形并证明:∠DBC = ∠BMA.18. 如图,在中, , 垂足为D,点E在上, , 垂足为F. (1)、求证:(2)、如果 , 求证: .19. 已知,在三角形ABC中,AD⊥BC于D,F是AB上一点,FE⊥BC于E,∠ADG=∠BFE
(1)、求证:(2)、如果 , 求证: .19. 已知,在三角形ABC中,AD⊥BC于D,F是AB上一点,FE⊥BC于E,∠ADG=∠BFE
 (1)、如图1,求证:DG∥AB(2)、如图2,若∠BAC=90°,请直接写出图中与∠CAD互余的角,不需要证明.20. 如图,已知∠1=∠2,∠BAC= 20°,∠ACF=80°.
(1)、如图1,求证:DG∥AB(2)、如图2,若∠BAC=90°,请直接写出图中与∠CAD互余的角,不需要证明.20. 如图,已知∠1=∠2,∠BAC= 20°,∠ACF=80°. (1)、求∠2的度数;(2)、请说明FC∥AD的理由.21. 如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)、求∠2的度数;(2)、请说明FC∥AD的理由.21. 如图,∠AGF=∠ABC,∠1+∠2=180°. (1)、试判断BF与DE的位置关系,并说明理由;(2)、若BF⊥AC,∠2=150°,求∠AFG的度数.22. 三角板是学习数学的重要工具 ,将一副三角板的直角顶点 C 按如图所示的方式叠放在一起, 当 时 ,且点 E 在直线AC 的上方时, 解决下列问题∶ (友情提示 ∶ ∠A=60°,∠D=30°,∠B=∠E=45°)
(1)、试判断BF与DE的位置关系,并说明理由;(2)、若BF⊥AC,∠2=150°,求∠AFG的度数.22. 三角板是学习数学的重要工具 ,将一副三角板的直角顶点 C 按如图所示的方式叠放在一起, 当 时 ,且点 E 在直线AC 的上方时, 解决下列问题∶ (友情提示 ∶ ∠A=60°,∠D=30°,∠B=∠E=45°) (1)、①若 ∠DCE=45°,求∠ACB;
(1)、①若 ∠DCE=45°,求∠ACB;②若∠ACB=140°,求∠DCE ;
(2)、由(1)猜想 ∠ACB与∠DCE的数量关系,并说明理由;(3)、这两块三角板是否存在一组边互相平行?若存在,请直接写出∠ACE的所有可能的值(不必说明理由);若不存在,请说明理由.
-