江西省上饶市、景德镇市六校2023届高三上学期理数10月联考试卷
试卷更新日期:2022-11-02 类型:月考试卷
一、单选题
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 著名数学家华罗庚曾说“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休”,在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数图象特征,则函数的图像大致是( )A、
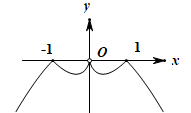 B、
B、 C、
C、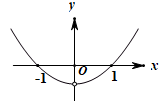 D、
D、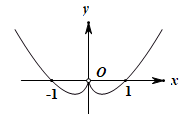 3. 已知函数 , 则不等式的解集为( )A、 B、 C、 D、4. 下列说法正确的是( )A、函数为实数集上的奇函效,当时,(a为常数),则 B、已知幂函数在单调递减,则实数 C、命题“ , ”的否定是“ , ” D、中.角A,B,C所对的边分别为a,b,c,则是的充分不必要条件5. 已知幂函数的图象过点(9,3),则函数在区间[1,9]上的值域为( )A、[-1,0] B、 C、[0,2] D、6. 函数在单调递减,且为奇函数.若 , 则满足的的取值范围是( )A、[-2,2] B、[-1,2] C、[0,4] D、[1,3]7. 函数的图象在处的切线对应的倾斜角为 , 则( )A、 B、 C、 D、.8. 已知函数 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件9. 若存在 , 使得不等式成立,则实数的取值范围是( )A、 B、 C、 D、10. 已知函数 , 若恒成立,则的最小值是( )A、 B、 C、 D、11. 已知函数是偶函数,且函数的图像关于点对称,当时, , 则( )A、-1 B、-2 C、0 D、212. 函数 , 定义域为 , 有唯一极值点,则实数a的取值范围为( )A、 B、 C、 D、
3. 已知函数 , 则不等式的解集为( )A、 B、 C、 D、4. 下列说法正确的是( )A、函数为实数集上的奇函效,当时,(a为常数),则 B、已知幂函数在单调递减,则实数 C、命题“ , ”的否定是“ , ” D、中.角A,B,C所对的边分别为a,b,c,则是的充分不必要条件5. 已知幂函数的图象过点(9,3),则函数在区间[1,9]上的值域为( )A、[-1,0] B、 C、[0,2] D、6. 函数在单调递减,且为奇函数.若 , 则满足的的取值范围是( )A、[-2,2] B、[-1,2] C、[0,4] D、[1,3]7. 函数的图象在处的切线对应的倾斜角为 , 则( )A、 B、 C、 D、.8. 已知函数 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件9. 若存在 , 使得不等式成立,则实数的取值范围是( )A、 B、 C、 D、10. 已知函数 , 若恒成立,则的最小值是( )A、 B、 C、 D、11. 已知函数是偶函数,且函数的图像关于点对称,当时, , 则( )A、-1 B、-2 C、0 D、212. 函数 , 定义域为 , 有唯一极值点,则实数a的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 若函数则与x轴围成的封闭图形的面积为.14. 若是函数的极值点,则方程在的不同实根个数为 .15. 将边长为的正三角形薄铁皮沿一条平行于某边的直线剪成两块,其中一块是梯形,记 , 则的最小值是 .16. 已知函数 , 若存在 , , 使得 , 则的取值范围是.
三、解答题
-
17. 已知命题:实数满足(其中);命题:实数满足 .(1)、若 , 为真命题,求实数的取值范围;(2)、若是的必要不充分条件,求实数的取值范围.18. 已知函数 , 求:(1)、求函数的单调区间;(2)、求函数在的最小值.19. 如图所示,将一个矩形花坛 扩建成一个更大的矩形花坛 ,要求 在射线 上, 在射线 上,且对角线 过 点,已知 米, 米,设 的长为 米.
 (1)、要使矩形 的面积大于54平方米,则 的长应在什么范围内?(2)、求当 的长度分别是多少时,矩形花坛 的面积最小,并求出此最小值.
(1)、要使矩形 的面积大于54平方米,则 的长应在什么范围内?(2)、求当 的长度分别是多少时,矩形花坛 的面积最小,并求出此最小值.