2022年秋季湘教版数学九年级期中复习检测B

试卷更新日期：2022-11-01 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 用配方法解一元二次方程 $3 x^{2} + 6 x - 1 = 0$ 时，将它化为 ${(x + a)}^{2} = b$ 的形式，则a+b的值为（）

A、 $\frac{10}{3}$ B、 $\frac{7}{3}$ C、2 D、 $\frac{4}{3}$

查看试题解析
2. 在平面直角坐标系中，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象如图所示，则一次函数 $y = k x + 2$ 的图象经过的象限是（）

A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四

查看试题解析
3. 如图，在△ABC中，D，E分别是AB和AC上的点，DE∥BC，若 $\frac{A D}{B D}$ ＝ $\frac{2}{1}$ ，那么 $\frac{D E}{B C}$ ＝（　　）

A、 $\frac{4}{9}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
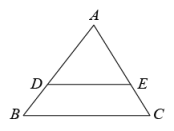4. 已知关于x的一元二次方程（m﹣1）x²+2x﹣3＝0有实数根，则m的取值范围是（）

A、m≥ $\frac{2}{3}$ B、m＜ $\frac{2}{3}$ C、m＞ $\frac{2}{3}$ 且m≠1 D、m≥ $\frac{2}{3}$ 且m≠1

查看试题解析
5. 如图，以点O为位似中心，作四边形 $A B C D$ 的位似图形 $A^{'} B^{'} C^{'} D^{'}$ ﹐已知 $\frac{O A}{O A^{'}} = \frac{1}{3}$ ，若四边形 $A B C D$ 的面积是2，则四边形 $A^{'} B^{'} C^{'} D^{'}$ 的面积是（）

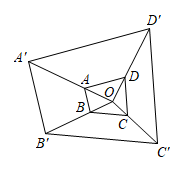A、4 B、6 C、16 D、18

查看试题解析
6. 如图，在函数 $y = \frac{2}{x} (x > 0)$ 的图象上任取一点A，过点A作y轴的垂线交函数 $y = - \frac{8}{x} (x < 0)$ 的图象于点B，连接OA，OB，则 $△ A O B$ 的面积是（）

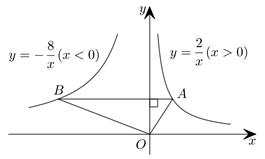A、3 B、5 C、6 D、10

查看试题解析
7. 已知 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - x - 2022 = 0$ 的两个实数根，则代数式 $x_{1}^{3} - 2022 x_{1} + x_{2}^{2}$ 的值是（）

A、4045 B、4044 C、2022 D、1

查看试题解析
8. 如图，在平面直角坐标系中， $C$ 为 $△ A O B$ 的 $O A$ 边上一点， $A C ： O C = 1 ： 2$ ，过 $C$ 作 $C D ∥ O B$ 交 $A B$ 于点 $D$ ， $C$ 、 $D$ 两点纵坐标分别为1、3，则 $B$ 点的纵坐标为（）

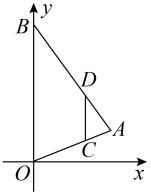A、4 B、5 C、6 D、7

查看试题解析
9. 如图，矩形OABC与反比例函数 $y_{1} = \frac{k_{1}}{x}$ （k₁是非零常数，x>0）的图象交于点M，N，与反比例函数 $y_{2} = \frac{k_{2}}{x}$ （k₂是非零常数，x>0）的图象交于点B，连接OM，ON．若四边形OMBN的面积为3，则k₁-k₂=（）

A、3 B、-3 C、 $\frac{3}{2}$ D、 $- \frac{3}{2}$

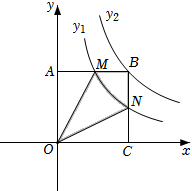查看试题解析
10. 如图，在正方形ABCD中，E，F是对角线AC上的两点，且EF＝2AE＝2CF，连接DE并延长交AB于点M，连接DF并延长交BC于点N，连接MN，则 $\frac{S_{△ AMD}}{S_{△ M B N}} =$ （）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、1 D、 $\frac{1}{2}$

查看试题解析

二、填空题（每题3分，共18分）

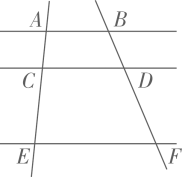
11. 如图， $A B / / C D / / E F$ ．若 $\frac{A C}{C E} = \frac{1}{2}$ ， $B D = 5$ ，则 $D F =$ ．

查看试题解析
12. 如图，小明同学用一张长11cm，宽7cm的矩形纸板制作一个底面积为 $21 c m^{2}$ 的无盖长方体纸盒，他将纸板的四个角各剪去一个同样大小的正方形，将四周向上折叠即可（损耗不计）．设剪去的正方形边长为xcm，则可列出关于x的方程为．

查看试题解析
13. 平面直角坐标系 $x O y$ 中，已知点 $A (m ， 6 m) ， B (3 m ， 2 n) ， C (- 3 m ， - 2 n)$ 是函数 $y = \frac{k}{x} (k \neq 0)$ 图象上的三点。若 $S_{△ A B C} = 2$ ，则k的值为．

查看试题解析
14. 如图，折叠边长为4cm的正方形纸片 $A B C D$ ，折痕是 $D M$ ，点 $C$ 落在点 $E$ 处，分别延长 $M E$ 、 $D E$ 交 $A B$ 于点 $F$ 、 $G$ ，若点 $M$ 是 $B C$ 边的中点，则 $F G =$ cm.

查看试题解析
15. 关于x的一元二次方程2x²+4mx+m=0有两个不同的实数根x₁ ， x₂ ，且 $x_{1}^{2} + x_{2}^{2} = \frac{3}{16}$ ，则m= ．

查看试题解析
16. 如图，反比例函数 $y = \frac{k}{x} (k > 0)$ 在第一象限的图象上有 $A (1 ， 6)$ ， $B (3 ， b)$ 两点，直线 $A B$ 与x轴相交于点C，D是线段 $O A$ 上一点．若 $A D \cdot B C = A B \cdot D O$ ，连接 $C D$ ，记 $△ A D C ， △ D O C$ 的面积分别为 $S_{1} ， S_{2}$ ，则 $S_{1} - S_{2}$ 的值为．

查看试题解析

三、解答题（共9题，共72分）

17. 解方程： $(2 x + 3)^{2} = (3 x + 2)^{2}$

查看试题解析
18. 已知：a是不等式 $5 (a - 2) + 8 < 6 (a - 1) + 7$ 的最小整数解，请用配方法解关于x的方程 $x^{2} + 2 a x + a + 1 = 0$ .

查看试题解析
19. 如图，一次函数 $y = k_{1} x + b$ 与反比例函数 $y = \frac{k_{2}}{x}$ 在第一象限交于 $M (2 ， 8)$ 、 $N$ 两点， $N A$ 垂直x轴于点 $A$ ， $O$ 为坐标原点，四边形 $O A N M$ 的面积为38．

(1)、求反比例函数及一次函数的解析式；

(2)、点P是反比例函数第三象限内的图象上一动点，请简要描述使 $△ P M N$ 的面积最小时点P的位置（不需证明），并求出点P的坐标和 $△ P M N$ 面积的最小值．

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - 3 m^{2} = 0$ .

(1)、求证：方程总有两个不相等的实数根；

(2)、若方程的两个实数根分别为 $α$ ， $β$ ，且 $α + 2 β = 5$ ，求 $m$ 的值.

查看试题解析
21. 如图，在菱形 $A B C D$ 中，点M，N分别是边 $B C$ ， $D C$ 上的点， $B M = \frac{3}{4} B C$ ， $D N = \frac{3}{4} D C$ ．连接 $A M$ ， $A N$ ，延长 $A N$ 交线段 $B C$ 延长线于点E．

(1)、求证： $△ A B M ≌ △ A N D$ ；

(2)、若AD=4，则ME的长是．

查看试题解析
22. 如图，正比例函数 $y = 4 x$ 与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于点 $A (a ， 4)$ ，点B在反比例函数图象上，连接AB，过点B作 $B C ⊥ x$ 轴于点 $C (2 ， 0)$ ．

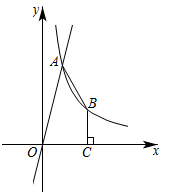(1)、求反比例函数解析式；

(2)、点D在第一象限，且以A，B，C，D为顶点的四边形是平行四边形，请直接写出点D的坐标．

查看试题解析
23. 商店准备销售一种多功能旅行背包，计划从厂家以每个30元的价格进货，经过市场发现当每个背包的售价为40元时，月均销量为280个，售价每增长2元，月均销量就相应减少20个．

(1)、若使这种背包的月均销量不低于130个，每个背包售价应不高于多少元？

(2)、在（1）的条件下，当这种背包销售单价为多少元时，销售利润是3120元？

(3)、这种背包的销售利润有可能达到3700元吗？若能，请求出此时的销售单价；若不能，请说明理由．

查看试题解析
24. 如图，点A在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上， $A B ⊥ x$ 轴，垂足为 $B (3 ， 0)$ ，过 $C (5 ， 0)$ 作 $C D ⊥ x$ 轴，交过B点的一次函数 $y = \frac{3}{2} x + b$ 的图象于D点，交反比例函数的图象于E点， $S_{△ A O B} = 3$ ．

(1)、求反比例函数 $y = \frac{k}{x} (x > 0)$ 和一次函数 $y = \frac{3}{2} x + b$ 的表达式：

(2)、求DE的长．

查看试题解析
25. 如图，在平行四边形 $A B C D$ 中， $A C$ 是一条对角线，且 $A B = A C = 5$ ， $B C = 6$ ， $E$ ， $F$ 是 $A D$ 边上两点，点 $F$ 在点 $E$ 的右侧， $A E = D F$ ，连接 $C E$ ， $C E$ 的延长线与 $B A$ 的延长线相交于点 $G$ ．

(1)、如图1， $M$ 是 $B C$ 边上一点，连接 $A M$ ， $M F$ ， $M F$ 与 $C E$ 相交于点 $N$ ．
①若 $A E = \frac{3}{2}$ ，求 $A G$ 的长；
②在满足①的条件下，若 $E N = N C$ ，求证： $A M ⊥ B C$ ；

(2)、如图2，连接 $G F$ ， $H$ 是 $G F$ 上一点，连接 $E H$ ．若 $∠ E H G = ∠ E F G + ∠ C E F$ ，且 $H F = 2 G H$ ，求 $E F$ 的长．

查看试题解析