2022年秋季湘教版数学九年级期中复习检测A
试卷更新日期:2022-11-01 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、
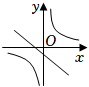 B、
B、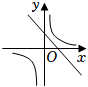 C、
C、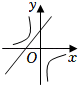 D、
D、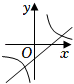 2. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )
2. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( ) A、5 B、6 C、 D、3. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )
A、5 B、6 C、 D、3. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )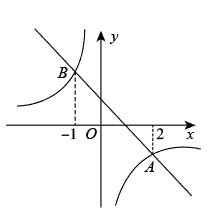 A、或 B、或 C、或 D、4. 对于实数 , 定义新运算: , 若关于的方程有两个不相等的实数根,则的取值范围( )A、 B、 C、且 D、且5. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A、或 B、或 C、或 D、4. 对于实数 , 定义新运算: , 若关于的方程有两个不相等的实数根,则的取值范围( )A、 B、 C、且 D、且5. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、6. 如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图像过点C,则k的值为( )
A、 B、 C、 D、6. 如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图像过点C,则k的值为( )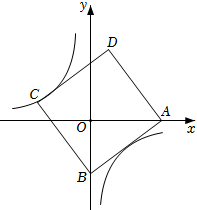 A、4 B、﹣4 C、﹣3 D、37. 受国际油价影响,今年我国汽油价格总体呈上升趋势.某地92号汽油价格三月底是6.2元/升,五月底是8.9元/升.设该地92号汽油价格这两个月平均每月的增长率为 , 根据题意列出方程,正确的是( )A、 B、 C、 D、8. 若关于x的一元二次方程有两个实数根 , , 且 , 则( )A、2或6 B、2或8 C、2 D、69. 如图,在四边形 中, , , , 平分 .设 , ,则 关于 的函数关系用图象大致可以表示为( )
A、4 B、﹣4 C、﹣3 D、37. 受国际油价影响,今年我国汽油价格总体呈上升趋势.某地92号汽油价格三月底是6.2元/升,五月底是8.9元/升.设该地92号汽油价格这两个月平均每月的增长率为 , 根据题意列出方程,正确的是( )A、 B、 C、 D、8. 若关于x的一元二次方程有两个实数根 , , 且 , 则( )A、2或6 B、2或8 C、2 D、69. 如图,在四边形 中, , , , 平分 .设 , ,则 关于 的函数关系用图象大致可以表示为( )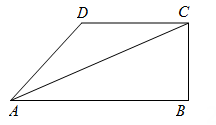 A、
A、 B、
B、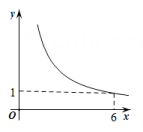 C、
C、 D、
D、 10. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:
10. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:① ;② ;③ ;④ ;⑤ .
其中正确的是( )
 A、①②③ B、①③④ C、①④⑤ D、②③④
A、①②③ B、①③④ C、①④⑤ D、②③④二、填空题(每题3分,共18分)
-
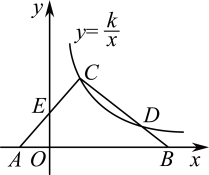
11. 、是关于的方程的两个实数根,且 , 则的值为 .12. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .
 13. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .
13. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .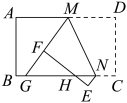 14. 关于x的一元二次方程2x2+4mx+m=0有两个不同的实数根x1 , x2 , 且 , 则m= .15. 如图,四边形OABC是平行四边形,点O是坐标原点,点C在y轴上,点B在反比例函数y=(x>0)的图象上,点A在反比例函数y=(x>0)的图象上,若平行四边形OABC的面积是7,则k= .
14. 关于x的一元二次方程2x2+4mx+m=0有两个不同的实数根x1 , x2 , 且 , 则m= .15. 如图,四边形OABC是平行四边形,点O是坐标原点,点C在y轴上,点B在反比例函数y=(x>0)的图象上,点A在反比例函数y=(x>0)的图象上,若平行四边形OABC的面积是7,则k= . 16. 如图,在中,点F、G在上,点E、H分别在、上,四边形是矩形,是的高. , 那么的长为 .
16. 如图,在中,点F、G在上,点E、H分别在、上,四边形是矩形,是的高. , 那么的长为 .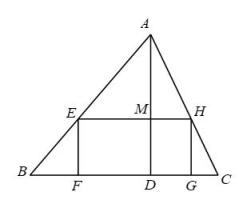
三、解答题(共9题,共72分)
-
17. 用配方法求的最大值,并求此时x的值.18. 阅读下列“问题”与“提示”后,将解方程的过程补充完整,求出x的值.
解方程:
提示:可以用“换元法”解方程.
解;设 , 则有.
原方程可化为:
续解:
19. 如图,在平面直角坐标系中,菱形的顶点在轴上, , 两点的坐标分别为 , , 直线:与反比例函数的图象交于 , 两点.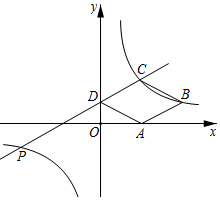 (1)、求该反比例函数的解析式及的值;(2)、判断点是否在该反比例函数的图象上,并说明理由.20. 如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE²=AQ·AB求证:
(1)、求该反比例函数的解析式及的值;(2)、判断点是否在该反比例函数的图象上,并说明理由.20. 如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE²=AQ·AB求证: (1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ21. 已知关于x的一元二次方程 有 , 两实数根.(1)、若 ,求 及 的值;(2)、是否存在实数 ,满足 ?若存在,求出求实数 的值;若不存在,请说明理由.22. 如图,双曲线y 与直线y=kx+b交于点A(﹣8,1)、B(2,﹣4),与两坐标轴分别交于点C、D,已知点E(1,0),连接AE、BE.
(1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ21. 已知关于x的一元二次方程 有 , 两实数根.(1)、若 ,求 及 的值;(2)、是否存在实数 ,满足 ?若存在,求出求实数 的值;若不存在,请说明理由.22. 如图,双曲线y 与直线y=kx+b交于点A(﹣8,1)、B(2,﹣4),与两坐标轴分别交于点C、D,已知点E(1,0),连接AE、BE. (1)、求m,k,b的值;(2)、求 ABE的面积;(3)、作直线ED,将直线ED向上平移n(n>0)个单位后,与双曲线y 有唯一交点,求n的值.23. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?24. 如图,一次函数的图像与反比例函数的图像交于点 , 与轴交于点 , 与轴交于点 , 轴于点 , , 点关于直线的对称点为点 .
(1)、求m,k,b的值;(2)、求 ABE的面积;(3)、作直线ED,将直线ED向上平移n(n>0)个单位后,与双曲线y 有唯一交点,求n的值.23. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?24. 如图,一次函数的图像与反比例函数的图像交于点 , 与轴交于点 , 与轴交于点 , 轴于点 , , 点关于直线的对称点为点 .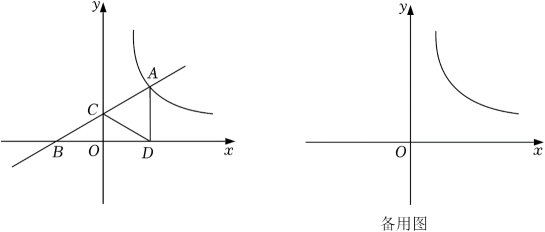 (1)、点是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.
(1)、点是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.①求、的值;
②若点在轴上,当最大时,求点的坐标.
25. 如图1,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE. (1)、判断线段BD与CE的数量关系并给出证明;(2)、延长ED交直线BC于点F.
(1)、判断线段BD与CE的数量关系并给出证明;(2)、延长ED交直线BC于点F.①如图2,当点F与点B重合时,直接用等式表示线段AE,BE和CE的数量关系为 ▲ ;
②如图3,当点F为线段BC中点,且ED=EC时,猜想∠BAD的度数,并说明理由.