甘肃省张掖市某重点校2022-2023学年高三上学期理数第一次月考试卷
试卷更新日期:2022-11-01 类型:月考试卷
一、单选题
-
1. 已知命题 , 则为( )A、 B、 C、 D、2. 已知集合 , , 则( )A、(-3,2] B、[-3,2) C、(2,3] D、[2,3)3. 已知函数 , (且),若 , 则( )A、 B、1 C、2 D、34. 我们知道,人们对声音有不同的感觉,这与声音的强度有关系.声音的强度常用 (单位:瓦/米2 , 即 )表示,但在实际测量时,声音的强度水平常用 (单位:分贝)表示,它们满足换算公式: ( ,其中 是人们平均能听到的声音的最小强度).若使某小区内公共场所声音的强度水平降低10分贝,则声音的强度应变为原来的( )A、 B、 C、 D、5. “lna<lnb”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 已知函数 .若 ,则 ( )A、4 B、3 C、2 D、17. 已知函数的图象如图所示,则下列说法与图象符合的是( )
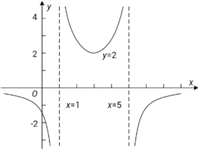 A、 B、 C、 D、8. 若偶函数在上单调递减, , , , 则、、满足( )A、 B、 C、 D、9. 已知函数满足:当时, , 且.若函数恰有5个零点,则( )A、-2 B、-1 C、0 D、110. 已知函数 , , 若成立,则的最小值为( )A、 B、 C、 D、11. 已知定义在 上的连续奇函数 的导函数为 ,当 时, ,则使得 成立的 的取值范围是( )A、 B、 C、 D、12. 定义“函数是上的级类周期函数” 如下: 函数 , 对于给定的非零常数 , 总存在非零常数 , 使得定义域内的任意实数都有( )恒成立,此时为的周期. 若是上的级类周期函数,且 , 当时, , 且是上的单调递增函数,则实数的取值范围为A、 B、 C、 D、
A、 B、 C、 D、8. 若偶函数在上单调递减, , , , 则、、满足( )A、 B、 C、 D、9. 已知函数满足:当时, , 且.若函数恰有5个零点,则( )A、-2 B、-1 C、0 D、110. 已知函数 , , 若成立,则的最小值为( )A、 B、 C、 D、11. 已知定义在 上的连续奇函数 的导函数为 ,当 时, ,则使得 成立的 的取值范围是( )A、 B、 C、 D、12. 定义“函数是上的级类周期函数” 如下: 函数 , 对于给定的非零常数 , 总存在非零常数 , 使得定义域内的任意实数都有( )恒成立,此时为的周期. 若是上的级类周期函数,且 , 当时, , 且是上的单调递增函数,则实数的取值范围为A、 B、 C、 D、二、填空题
-
13. 已知函数为上的偶函数,则 .14. 若函数与的图象在一个公共点处的切线相同,则实数 .15. 函数在区间上的最大值是.16. 设函数 , 集合 , , 若 , 则实数的取值构成的集合是.
三、解答题
-
17. 设函数的定义域为集合 , 集合.(1)、若 , 求;(2)、若 , 且 , 求.18. 已知函数有两个零点 , , 且 , 的倒数和为-1.(1)、求函数的解析式;(2)、若在区间上,不等式恒成立,求实数的取值范围.19. 已知:函数的定义域为 , :存在 , 使得不等式成立.(1)、若为真,求实数的取值范围.(2)、若为真且为假,求实数的取值范围.