福建省百校联考2023届高三上学期数学第一次联考试卷
试卷更新日期:2022-11-01 类型:月考试卷
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,3. 青花瓷,又称白地青花瓷,常简称青花,是中国瓷器的主流品种之一.如图,这是景德镇青花瓷,现往该青花瓷中匀速注水,则水的高度与时间的函数图象大致是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 在四边形中, , 则“”是“四边形为直角梯形”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知 , , 直线与曲线相切,则的最小值是( )A、16 B、12 C、8 D、46. , 则( )A、 B、 C、 D、7. 定义在R上的偶函数满足 , 且当时, , 则( )A、-4 B、-3 C、3 D、08. 已知 , , 则( )A、 B、 C、 D、
4. 在四边形中, , 则“”是“四边形为直角梯形”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知 , , 直线与曲线相切,则的最小值是( )A、16 B、12 C、8 D、46. , 则( )A、 B、 C、 D、7. 定义在R上的偶函数满足 , 且当时, , 则( )A、-4 B、-3 C、3 D、08. 已知 , , 则( )A、 B、 C、 D、二、多选题
-
9. 已知函数有两个极值点 , 则( )A、是的极大值点, 是的极小值点 B、 C、 D、10. 已知函数)的部分图像如图所示,则( )
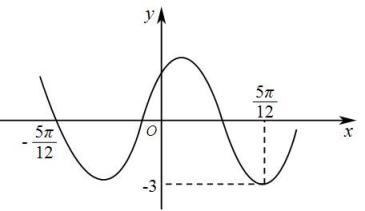 A、 , , B、 C、直线是图像的一条对称轴 D、函数在上单调递减11. 若 , 则( )A、 B、 C、 D、12. 已知 , , , 则( )A、 B、 C、 D、
A、 , , B、 C、直线是图像的一条对称轴 D、函数在上单调递减11. 若 , 则( )A、 B、 C、 D、12. 已知 , , , 则( )A、 B、 C、 D、三、填空题
-
13. 所数的定义域是.14. 函数( , 且)的图象过定点.则点的坐标是.15. 已知正数 , 满足① , ②两个条件中的一个,则的最小值为.16. 已知函数若方程有5个不同的实数解,则实数a的取值范围为 .
四、解答题
-
17. 设集合 , .(1)、当时,求;(2)、若 , 求的取值范围.18. 已知幂函数在上是减函数.(1)、求的解析式;(2)、若 , 求的取值范围.19. 已知函数 .(1)、若在上有且仅有2个极值点,求的取值范围;(2)、将的图象向右平移个单位长度后,再将所得图象各点的横坐标缩短为原来的 , 纵坐标不变,得到函数的图象,若的最小正周期为 , 求的单调递减区间.20. 据国家气象局消息,今年各地均出现了极端高温天气.漫漫暑期,空调成了很好的降温工具,而物体的降温遵循牛顿冷却定律.如果某物体的初始温度为 , 那么经过分钟后,温度满足 , 其中为室温,为半衰期.为模拟观察空调的降温效果,小明把一杯的茶水放在的房间,10分钟后茶水降温至.(参考数据:)(1)、若欲将这杯茶水继续降温至 , 大约还需要多少分钟?(保留整数)(2)、为适应市场需求,2022年某企业扩大了某型号的变频空调的生产,全年需投入固定成本200万元,每生产千台空调,需另投入成本万元,且已知每台空调售价3000元,且生产的空调能全部销售完.问2022年该企业该型号的变频空调的总产量为多少千台时,获利最大?并求出最大利润.