天津市南开区2021-2022学年七年级上学期期末考试数学试题
试卷更新日期:2022-11-01 类型:期末考试
一、单选题
-
1. 已知A地的海拔高度为-36米,B地比A地高20米,则B地的海拔高度为( )A、16米 B、20米 C、-16米 D、-56米2. 在数 ,0, , , 中,正数的个数为( )A、2 B、3 C、4 D、53. 据Worldmeters实时统计数据显示,截至北京时间2021年10月3日,全球累计确诊新冠肺炎病例约达235000000例,数据235000000用科学记数法表示为( )A、2.35×108 B、2.35×109 C、235×106 D、0.235×1094. 单项式﹣a3b的系数与次数分别是( )A、﹣ , 3 B、 , 4 C、﹣ , 4 D、﹣2,35. 如图,虚线左边的图形绕虚线旋转一周,能形成的几何体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“负”相对的面上的汉字是( )
6. 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“负”相对的面上的汉字是( )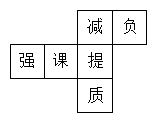 A、强 B、课 C、提 D、质7. 当分针指向12,时针这时恰好与分针成30°的角,此时是( )A、9点钟 B、10点钟 C、11点钟或1点钟 D、2点钟或10点钟8. 根据直线、射线、线段的性质,图中的各组直线、射线、线段一定能相交的是( )A、
A、强 B、课 C、提 D、质7. 当分针指向12,时针这时恰好与分针成30°的角,此时是( )A、9点钟 B、10点钟 C、11点钟或1点钟 D、2点钟或10点钟8. 根据直线、射线、线段的性质,图中的各组直线、射线、线段一定能相交的是( )A、 B、
B、 C、
C、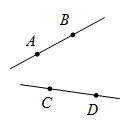 D、
D、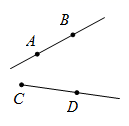 9. 下列关于多项式 - 3a2b + ab - 2的说法中,正确的是( )A、是二次三项式 B、二次项系数是0 C、常数项是2 D、最高次项是 - 3a2b10. 一种商品每件成本为a元,原来按成本增加40%定出售价,现在由于库存积压减价,打八折出售,则每件盈利( )元.A、0.1a B、0.12a C、0.15a D、0.2a11. 用式子表示“比x的3倍小5的数等于x的4倍”为( )A、3x﹣5=4x B、5﹣3x=4x C、 x﹣5=4x D、3x﹣5= x12. 如图. , 、分别是∠AOM和∠MOB的平分线,、分别是和的平分线,、分别是和的平分线,…,、分别是和的平分线,则的度数是( )
9. 下列关于多项式 - 3a2b + ab - 2的说法中,正确的是( )A、是二次三项式 B、二次项系数是0 C、常数项是2 D、最高次项是 - 3a2b10. 一种商品每件成本为a元,原来按成本增加40%定出售价,现在由于库存积压减价,打八折出售,则每件盈利( )元.A、0.1a B、0.12a C、0.15a D、0.2a11. 用式子表示“比x的3倍小5的数等于x的4倍”为( )A、3x﹣5=4x B、5﹣3x=4x C、 x﹣5=4x D、3x﹣5= x12. 如图. , 、分别是∠AOM和∠MOB的平分线,、分别是和的平分线,、分别是和的平分线,…,、分别是和的平分线,则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知∠1与∠2互余,∠3与∠2互余,则∠1∠3.(填“>”,“=”或“<”)14. 若 , , 则 .15. 若点C是直线AB上的一点,且线段AC=3,BC=7,则线段AB的长为 .16. 已知|m|=m+1,则(4m﹣1)4= .17. 古书《九章算术》有这样一个问题:“今有共买鸡,人出九,盈十一;人出六,不足十六,问人数、鸡价各几何?”大意是:有几个人共同出钱买鸡,每人出9钱,则多了11钱,每人出6钱,则少了16钱,那么有几个人共同买鸡?鸡的总价是多少?若有x个人共同买鸡,则可列方程: .18. 有若干个数,第一个数记为 ,第二个数记为 ,…,第 个数记为 .若 ,从第二个数起,每个数都等于“1与它前面那个数的差的倒数”, .
三、解答题
-
19.(1)、解方程:(2)、解方程:20. 已知代数式A=﹣6x2y+4xy2﹣5,B=﹣3x2y+2xy2﹣3(1)、求A﹣B的值,其中|x﹣1|+(y+2)2=0(2)、请问A﹣2B的值与x,y的取值是否有关系,试说明理由.21. 已知一个角的余角比这个角的补角的一半还小12°,求这个角的度数.22. 已知:线段AB=20cm,点C为线段AB上一点,BC=4cm,点D、点E分别为AC和AB的中点,求线段DE的长.
 23. 甲、乙两人从A,B两地同时出发,甲骑自行车,乙开汽车,沿同一条路线相向匀速行.
23. 甲、乙两人从A,B两地同时出发,甲骑自行车,乙开汽车,沿同一条路线相向匀速行.出发后经3小时两人相遇.已知在相遇时乙比甲多行了90千米,相遇后经1小时乙到达A地问:
(1)、甲车速度是千米/小时,乙车速度是千米/小时.A,B距离是千米.(2)、这一天,若乙车晚1小时出发,则再经过多长时间,两车相距20千米?24. 已知:如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=1:5.将一等腰直角三角板的直角顶点放在点O处,一直角边ON在射线OB上,另一直角边OM在直线AB的下方. (1)、将图1中的等腰直角三角板绕点O以每秒3°的速度逆时针方向旋转一周,直角边ON旋转后的对应边为ON',直角边OM旋转后的对应边为OM'.在此过程中,经过t秒后,OM'恰好平分∠BOC,求t的值;(2)、如图2,在(1)问的条件下,若等腰直角三角板在转动的同时,射线OC也绕点O以每秒4°的速度顺时针方向旋转,射线OC旋转后的对应射线为OC'.当射线OC'落在射线OC的反向延长线上时,射线OC和等腰直角三角板同时停止运动.在此过程中,是否存在某一时刻t,使得OC'//M'N'.若存在,请求出t的值,若不存在,诮说明理由;(3)、如图3,在(1)问的条件下,若等腰直角三角板在转动的同时,射线OC也绕点O以每秒5°的速度顺针方向旋转,射线OC旋转后的对应射线为OC'.当等腰直角三角板停止运动时,射线OC也停止运动.在整个运动过程中.经过l秒后,∠M'ON'的某一边恰好平分∠AOC',请直接写出所有满足条件的t的值.
(1)、将图1中的等腰直角三角板绕点O以每秒3°的速度逆时针方向旋转一周,直角边ON旋转后的对应边为ON',直角边OM旋转后的对应边为OM'.在此过程中,经过t秒后,OM'恰好平分∠BOC,求t的值;(2)、如图2,在(1)问的条件下,若等腰直角三角板在转动的同时,射线OC也绕点O以每秒4°的速度顺时针方向旋转,射线OC旋转后的对应射线为OC'.当射线OC'落在射线OC的反向延长线上时,射线OC和等腰直角三角板同时停止运动.在此过程中,是否存在某一时刻t,使得OC'//M'N'.若存在,请求出t的值,若不存在,诮说明理由;(3)、如图3,在(1)问的条件下,若等腰直角三角板在转动的同时,射线OC也绕点O以每秒5°的速度顺针方向旋转,射线OC旋转后的对应射线为OC'.当等腰直角三角板停止运动时,射线OC也停止运动.在整个运动过程中.经过l秒后,∠M'ON'的某一边恰好平分∠AOC',请直接写出所有满足条件的t的值.