山西省阳泉市盂县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-01 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 围成下列这些立体图形的各个面中，都是平的面为（    ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 表格是2021年12月21日我国几个城市的最低气温，在这些城市中，最低气温最低的城市是（    ）

    城市

    北京

    上海

    沈阳

    海南

    太原

    新疆

    最低气温

    −3℃

    7℃

    ﹣13℃

    15℃

    ﹣10℃

    ﹣6℃

    A、北京 B、沈阳 C、太原 D、上海

    查看试题解析

  • 3. 多项式2x2－x＋1的各项分别是（    ）
    A、

    二次项

    一次项

    常数项

    2x2

    x

    0

     B、

    二次项

    一次项

    常数项

    2x2

    -x

    1

     C、

    二次项

    一次项

    常数项

    -2x2

    x

    -1

     D、

    二次项

    一次项

    常数项

    2

    -1

    1

    查看试题解析

  • 4. 中国人对方程的研究有悠久的历史．中国古代数学著作《九章算术》中有专门以“方程”命名的一章．中国古代数学家表示方程时，只用算筹表示各未知数的系数，而没有使用专门的记法来表示未知数.1859年中国清代一位数学家在翻译外国数学著作时，开始将equation（指含未知数的等式）一词译为“方程”，至今一直这样沿用，这位清代数学家是（ ）
    A、花拉子米 B、李治 C、李善兰 D、刘徽

    查看试题解析

  • 5. 根据下面所给条件，能列出方程的是（    ）
    A、一个数的13是6 B、x与1的差的14 C、甲数的2倍与乙数的13 D、a与b的和的60%

    查看试题解析

  • 6. 小明晚上放学到家时，钟表的时间显示为6点15分（如图），此时时钟的分针与时针所成角的度数是（    ）

    A、90° B、92.5° C、97.5° D、102.5°

    查看试题解析

  • 7. 若a、b表示非零常数，整式ax+b的值随x的取值而发生变化，如下表

    x

    -3

    -1

    0

    1

    3

    ……

    ax+b

    -3

    1

    3

    5

    9

    ……

    则关于x的一元一次方程−ax−b=−3的解为（    ）

    A、x=−3 B、x=−1 C、x=0 D、x=3

    查看试题解析

  • 8. 数学活动课上，“智慧小组”设计用一个大长方形制作一个长方体纸盒，如图所示，要求纸盒的长、宽、高分别为4、3、1，则这个大长方形的长为（    ）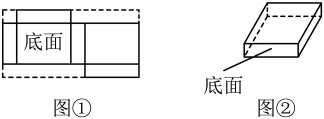

    A、14 B、10 C、8 D、7

    查看试题解析

  • 9. 我们这样研究一个数的绝对值的性质：当a＞0时，如|a|=|2|=2，此时a的绝对值是它本身；当a=0时，如|a|=0，此时a的绝对值是0；当a＜0时，如|a|=|﹣2|=2，此时a的绝对值是它的相反数．这种分析问题的方法所体现的数学思想是（    ）
    A、分类讨论思想 B、公理化思想 C、数形结合思想 D、转化思想

    查看试题解析

  • 10. 如图，在2022年2月的月历表中，任意圈出表中竖列上相邻的三个数，请你运用方程思想来研究，发现这三个数的和不可能是（    ）

    一

    二

    三

    四

    五

    六

    日


    1

    2

    3

    4

    6

    7

    8

    9

    10

    11

    13

    14

    15

    16

    17

    18

    20

    21

    22

    23

    24

    25

    26

    27

    28

    A、24 B、45 C、60 D、69

    查看试题解析

二、填空题

  • 11. 写出一个关于x的一元一次方程是 ．

    查看试题解析

  • 12. 单项式﹣x2的系数是 ．

    查看试题解析

  • 13. 每框杨梅以5千克为基准，超过的千克数记为正数，不足的千克数记为负数，记录如图，则这4框杨梅的总质量是千克．

    查看试题解析

  • 14. 下列三个现象：

    ①用两个钉子就可以把一根木条固定在墙上；

    ②从A地到B地架设电线，只要尽可能沿着线段AB架设，就能节省材料；

    ③植树时，只要定出两棵树的位置，就能使同一行树在一条直线上．

    其中可用“两点之间，线段最短”来解释的现象有(填序号)．

    查看试题解析

  • 15. 体育课上的口令：立正，向右转，向后转，向左转之间可以相加．连续执行两个口令就把这两个口令加起来．例如：向右转＋向左转=立正；向左转＋向后转=向右转．如果分别用0，1，2，3分别代表立正，向右转，向后转，向左转，就可以用如图所示的加法表来表示，在表中填了部分的数值和代表数值的字母．下列对于字母a，b，c，d的值，有如下说法小红说a=0，小强说b=1，小亮说c=2，小龙说d=3．你认为的说法是错误的．

    +

    0

    1

    2

    3

    0

    0

    1

    2

    3

    1

    1

    2

    3

    2

    2

    d

    3

    3

    a

    b

    查看试题解析

三、解答题

  • 16.    
    (1)、计算：2－|﹣3|÷13；
    (2)、解方程：4x−2=2＋3x．

    查看试题解析

  • 17. 如图是由大小相同的小立方体搭成的几何体．请在下面方格纸中分别画出从正面、左面、上面看到该几何体的形状图．

    查看试题解析

  • 18. 老师在黑板上出了一道解方程的题：x2−x−13＝1，小明同学的解法如下：

    解：方程两边同乘6，得 3x- 2 (x - 1)=6①

    去括号，得3x - 2x- 2=6②

    合并同类项，得x -2=6③

    解得x=84

    原方程的解为x=8⑤

    (1)、上述解答过程中的第一步是 ， 依据是；
    (2)、从第步出现错误（填序号），错误原因是；
    (3)、请直接写出方程的解： ．

    查看试题解析

  • 19. 通过有理数运算的学习，我们知道运算法则能指导我们如何运算，运算律则使运算简便．请用运算律计算：
    (1)、﹣2.4＋3.5－4.6＋3.5；
    (2)、50×37＋50×（﹣17）＋50×57 ．

    查看试题解析

  • 20. “春节”期间，小明一家人乘坐高铁前往某市旅游，计划第二天开始租用新能源汽车自驾出游，经了解，甲、乙两公司的收费标准如下：

    甲公司：一次性收取固定租金80元，另外再按租车时间计费，每小时的租费是15元；

    乙公司：无固定租金，直接以租车时间收费，每小时的租费是30元．

    (1)、若租车时间为x小时，则租用甲公司的车所需费用为元，租用乙公司的车所需费用为元(结果用含x的代数式表示)；
    (2)、当租车时间为11小时时，选择哪一家公司比较合算？
    (3)、当租车多少时间时，两家公司收费相同？

    查看试题解析

  • 21. 先阅读下面材料，再完成任务

    【材料】下列等式：4－35=4×35＋1，7－34=7×34＋1，…，具有a－b=ab＋1的结构特征，我们把满足这一特征的一对有理数称为“共生有理数对”，记作(a，b)，例如：(4，35)、(7，34)都是“共生有理数对”．

    (1)、在两个数对(﹣2，1)、(2，13)中，“共生有理数对”是；
    (2)、请再写出一对“共生有理数对”；（要求：不与题目中已有的“共生有理数对”重复）
    (3)、若(x，﹣2)是“共生有理数对”，求x的值；
    (4)、若(m，n)是“共生有理数对”，判断(﹣n，﹣m)“共生有理数对” ． （填“是”或“不是”）

    查看试题解析

  • 22. 操作与实践：在综合与实践活动课上，老师将一副三角板按图1所示的位置摆放，分别在∠AOC，∠BOD的内部作射线OM，ON，然后提出如下问题：先添加一个适当条件，再求∠MON的度数．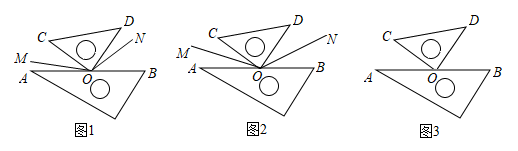

    (1)、特例探究：“兴趣小组”的同学添加了：“若OM，ON分别平分∠AOC，∠BOD”，画出如图2所示图形．小组3号同学佳佳的做法：由于图中∠AOC与∠BOD的和为90°，所以我们容易得到∠MOC与∠NOD的和，这样就能求出∠MON的度数．请你根据佳佳的做法，写出解答过程．
    (2)、特例探究：“发现小组”的同学添加了：“若∠MOC=13∠AOC，∠DON=13∠BOD”，画出如图3所示图形．小组2号同学乐乐的做法：设∠AOC的度数为x°，我们就能用含有x°的式子表示出∠COM和∠DON的度数，这样就能求出∠MON的度数，请你根据乐乐的做法，写出解答过程．
    (3)、类比拓展：受“兴趣小组”和“发现小组”的启发，“创新小组”的同学添加了：“若∠MOC=1n∠AOC，∠DON=1n∠BOD”．请你直接写出∠MON的度数．

    查看试题解析

  • 23. 综合探究

    【背景知识】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：如图①，若数轴上点A、点B表示的数分别为a，b（b＞a），则线段AB的长（点A到点B的距离）可表示为b－a．请用上面材料中的知识解答下面的问题：

    【问题情境】如图②，一个点从数轴上的原点开始，先向左移动2个单位长度到达点A，再向右移动3个单位长度到达点B，然后再向右移动5个单位长度到达点C．

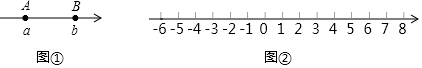    (1)、【问题探究】请在图②中表示出A、B、C三点的位置；
    (2)、【问题探究】若点P从点A出发，以每秒1个单位长度的速度沿数轴向左匀速运动，同时点M、N从点B、点C分别以每秒2个单位长度、每秒3个单位长度速度沿数轴向右匀速运动．设移动时间为t秒(t＞0)．

    ①A，B两点间的距离AB=      ▲  ， AC=      ▲ ；

    ②若点D、E分别是线段AB，BC的中点，求线段DE的长；

    ③用含t的代数式表示：t秒时，点P表示的数为      ▲  ， 点M表示的数为      ▲  ， 点N表示的数为      ▲ ；

    ④试探究在移动的过程中，3PN－4PM的值是否随着时间t的变化而变化？若变化说明理由；若不变，请求其值．

    查看试题解析